Глава 5. Аналитическое описание табличных зависимостей

5.1. Постановка задачи

Пусть известное значение некоторой функции f образуют следующую таблицу:

x	x0	x1	x2	…	xn
f(x)	y0	y1	y2	…	yn

при этом требуется получить значение функции f для такого значения аргумента x, которое принадлежит отрезку [x,x], но не совпадает ни с одним из значений x_i, i=0,1,…,n.

Очевидный прием решения – вычислить значение функции f(x), воспользовавшись аналитическим выражением функции f.

Этот прием, однако, можно применить лишь в случае, когда аналитически выражение f пригодно для вычислений. Более того, часто аналитические выражения функции f вовсе не известны.

В этих случаях применяется особый прием – построение по исходной информации (табличным значениям) приближающей функции F, которая в некотором смысле близка к функции f, и аналитическим выражением которой можно воспользоваться для вычисления функции приближенно.

f(x)=F(x)

(1)

При построении приближающей функции используют один из двух подходов: интерполирование или аппроксимирование функции. Если исходные данные (табличные значения функции) имеют стабильную природу (т.е. для одного и того же значения аргумента, функция всегда принимает одно и то же значение), то требуют строго совпадения значений исходной функции f(x) и получаемой функции F(x) в точках x_i, i=0,1,2,…,n:

F(x0)=y0, F(x1)=y1, …, F(xn)=yn

(2)

В этом случае нахождение приближенной функции называют интерполяцией или интерполированием, а точки x₀, x₁,…,x_n – узлами интерполяции.

Если же исходные данные носят случайный характер, то накладывать такое требование бессмысленно, т.к. исходная функция при одном и том же значении аргумента может принимать различные значения, лежащие в некотором доверительном интервале. В этом случае получают сравнительно простое аналитическое выражение функции, причем, при подстановке в это аналитическое выражение табличных значений аргумента, должны получаться значения F(x_i), попадающие в указанный доверительный интервал. Данный подход называют аппроксимацией функции.

Рассмотрим каждый из подходов подробнее.

Интерполяция

Будем искать интерполирующую функцию F(x) в виде многочлена степени n

(3)

Этот многочлен имеет n+1 коэффициент. Естественно предположить, что n+1 условий (2), наложенных на многочлен, позволят однозначно определить его коэффициенты. Т.к. требуя для P_n(x) выполнения условий (2) получаем систему из n+1 уравнений с n+1 неизвестными:

(4)

Решая эту систему относительно неизвестных мы и получим аналитическое выражение полинома (3).

Система (4) всегда имеет единственное решение, так как ее определитель известный в алгебре как определитель Вандермонда, отличен от нуля:

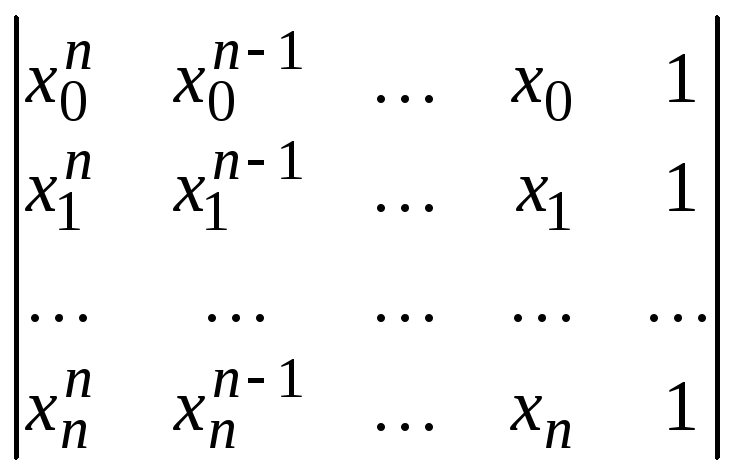
Отсюда следует, что интерполяционный многочлен P_n(x) для функции f, заданной таблицей существует и единствен.

Может случиться так, что какие-то коэффициенты в P_n(x), в том числе и a_n, равны нулю, поэтому интерполяционный полином при рассмотренных условиях в общем случае имеет степень не большую, чем n.

Описанный прием в принципе можно было бы использовать и для практического решения задач интерполирования многочленом. Однако на практике используются другие, более удобные и менее трудоемкие способы.