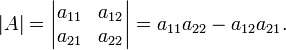1.Асимптоти. Якщо для функції існує така пряма, що віддаль від точки графіка функції до цієї прямої прямує до нуля при безмежному віддаленні точки від початку координат, то ця пряма називається асимптотою графіка функції.

Пряма є вертикальною асимптотою графіка функції , якщо або Неперервні функції не мають вертикальних асимптот.

Якщо ж координата точки прямує до або , то графік функції має похилу асимптоту для існування якої необхідно і достатньо існування двох скінченних границь

і

2. Лінійні операції над векторами. Вектором (геометричним вектором) називається множина всіх направлених відрізків, що мають однакову довжину і напрямок. Довжина відрізка називається довжиною (модулем) вектора і позначається символом Вектор нульової довжини називається нульовим вектором і позначається символом

Два вектори і називаються колінеарними, якщо вони знаходяться на паралельних прямих

Три вектори називаються компланарними, якщо вони паралельні деякій площині або лежать в одній площині.

Добутком вектора на дійсне число називається такий вектор, що:

1)

2) вектори і співнаправлені при >0 і протилежні при <0.

Сума двох векторів визначається за правилом паралелограма (рис.1.1) або за правилом трикутника.

Якщо то вектор називається протилежним вектору і позначається символом Різницею двох векторів називається такий вектор що дорівнює

5.Функція називається нескінченно малою при якщо Функція називається нескінченно великою при якщо Нехай і нескінченно малі при і то: при нескінченно малі і називаються нескінченно малими одного порядку; при називають нескінченно малою вищого порядку ніж і пишуть ; при нескінченно малі і називаються еквівалентними і пишуть ~.

Якщо і нескінченно малі функції при і

~ а ~ то

3.Віддаль від точки до площини Віддаль від точки до площини-це число d(Mo,P)=(MoM’ ) ,де М’ – ортогональна проекція точки Мо на площину Р

Якщо площина задана загальним рівнянням у вигляді, то віддаль від точки до площини обчислюється

за формулою

4.Віддаль між двома заданими точками

Для будь-яких точок A (a) і B (b) координатної прямої відстань AB дорівнює модулю різниці координат цих точок, тобто

6.Властивості визначників:

1)         det А=йЛ Ат, тобто визначник не змінюється при транспонуванні матриці;

2)         якщо одна стрічка визначника складається лише з нупів, то визначник рівний иупю (те ж саме відноситься до стовпця);

3)         при перестановці двох стрічок (стовпців) місцями визначник змінює знак;

4)         визначник, що містить дві однакові стрічки (стовпці) рівний нупю;

5)         якщо всі елементи деякої стрічки визначника помножиги на довільне число к то сам визначник помножиться на це ж число;

наслідок: спільний множник всіх елементів стрічки або стовпця можна винес-ти за знак визначника;

6)         визначник, який містить дві пропорційні стрічки (стовгщі) рівний нупю;

7)         якщо до елементів однієї стрічки (стовпця) додати елементи ішпої (можливо домножені на деякий коефіцієнт), то визначник не зміниться;

8)         визначник трикугної матриці рівний добугку елементів, які розміщені на го-ловнійдіагоналі матрщі;

9)         визначник добугку матрщь рівний добугку визначників матриць

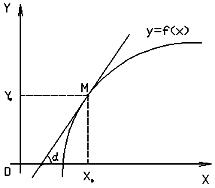
7. Геометричний зміст похідної

v(t) = S'(t).

Геометричний зміст похідної: значення похідної функції y = f(x) у точці x0 дорівнює кутовому коефіцієнту дотичної до графіка функції в точці з абсцисою x0: y' = f'(x0) = k = tgα.

8. Горизонтальна асимптота - пряма виду за умови існування межі.

Горизонтальна асимптота є частковим випадком похилої при k = 0.

Дослідження асимптот дозволяє чіткіше уявити поведінку графіка функції,

оскільки властивості функції поблизу її асимптоти дуже близькі до

властивостей асимптоти — лінійної функції, властивості якої добре

вивчені. Систематичне використання цієї властивості породило напрямок у

сучасній математиці — «асимптотичні методи дослідження».

9. Матриця — математичний об'єкт, записаний у вигляді прямокутної таблиці чисел (чи елементів кільця) і допускаючий операції (додавання, віднімання, множення та множення на скаляр). Зазвичай матриці представляються двовимірними (прямокутними) таблицями. Іноді розглядають багатовимірні матриці або матриці непрямокутної форми. В даній статті вони розглядатися не будуть.

Горизонтальні лінії в матриці звуть рядками, вертикальні — стовпцями.

Матрицю, що складається з m рядків та n стовпців, називають матрицею m-на-n (або mn-матрицею), а m і n — її розмірністю.

Елемент матриці A, що знаходиться на перетині i-го рядка з j-им стовпчиком, називають i,j-им елементом або (i,j)-им елементом A.

Записують це як A_i,j чи A[i,j], або, в нотації мови програмування C, A[i][j].

Часто пишуть для означення матриці A розмірності n x m, де кожен елемент матриці A[i,j] позначають як a_ij для всіх 1 ≤ i ≤ n та 1 ≤ j ≤ m.

Додавання

Якщо дано дві матриці m-на-n A і B, можемо означити їх суму A + B як матрицю m-на-n, що утворюється додаванням відповідних елементів, себто, (A + B)[i, j] = A[i, j] + B[i, j]. Наприклад,

Множення на скаляр

Якщо дано матрицю A і число c, можемо означити множення на скаляр cA як (cA)[i, j] = cA[i, j]. Наприклад,

З цими двома операціями множина M(m, n, R) усіх матриць m-на-n з дійсними елементами є дійсним векторним простором розмірності mn.

Множення матриць

Множення двох матриць має сенс лише тоді, коли число стовпчиків першої матриці дорівнює числу рядків другої матриці. Якщо A — матриця m-на-n (m рядків, n стовпчиків), а B — матриця n-на-p (n рядків, p стовпчиків), їх добуток AB є матрицею m-на-p (m рядків, p стовпчиків), що розраховується за формулою:

(AB)[i, j] = A[i, 1] * B[1, j] + A[i, 2] * B[2, j] + ... + A[i, n] * B[n, j] для кожної пари i та j.

10. Визначник— одна з найважливіших характеристик квадратних матриць.

Визначник 2×2 матриці

Щоб знайти визначник матриці, множимо елементи головної діагоналі та віднімаємо добуток елементів побічної діагоналі: