6.1. Предел числовой последовательности

Определение. Если по некоторому закону каждому натурально­му числу п поставлено в соответствие вполне определенное число а_п, то говорят, что задана числовая последовательность {а_п}:

(не монотонная, ограниченная). Рассмотрим числовую последовательность (6.1). Изобразим ее члены точками числовой оси (рис. 6.1).

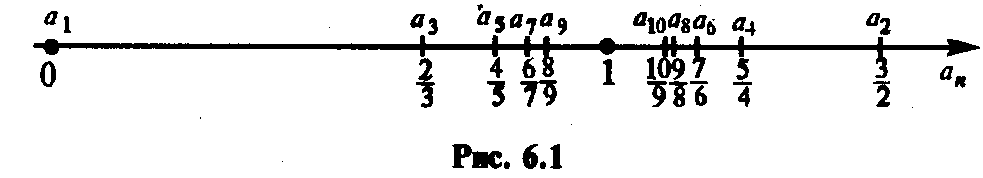
Можно заметить, что члены последовательности а„ с ростом п как угодно близко приближаются к 1. При этом абсолютная ве­личина разности \а_п -1| становится все меньше и меньше.

т.е. с ростом п \ап -1| будет меньше любого, сколь угодно малого положительного числа.

Определение. Число А называется пределом числовой последо-вательности {яя}, если для любого, даже сколь угодно малого по-ложительного числа £>0, найдется такой номер N (зависящий от s, N= N(e))9 что для всех членов последовательности с номерами n>N верно неравенство

\ап-А\<ъ. (6.2)

6.2. Предел функции в бесконечности и в точке

Предел функции в бесконечности. С понятием предела число¬вой последовательности an=fin) тесно связано понятие предела

функции у— fix) в бесконечности. Если в первом случае пере¬менная л, возрастая, принимает лишь целые значения, то во вто¬ром случае переменная х, изменяясь, принимает любые значения.

Определение. Число А называется пределом функции у— f(x) при х9 стремящемся к бесконечности, если для любого, даже сколь угодно малого положительного числа е>0, найдется такое положи¬тельное число S >0 (зависящее от е; S=8(€))9 что для всех х таких, что \x\>S, верно неравенство:

Предел функции в точке. Пусть функция y=fix) задана в неко¬торой окрестности точки х0, кроме, быть может, самой точки х0.

Определение. Число А называется пределом функции fix) при х, стремящемся к XQ (или в точке XQ ), если для любого, даже сколь угодно малого положительного числа е>0, найдется такое положи-тельное число 5>0 (зависящее от е, .5=5(8», что для всех х, не рав¬ных х0 и удовлетворяющих условию

I х-х0 |<5, (6.4)

выполняется неравенство

\Лх)-А |<в. (6.5)

Этот предел функции обозначается lim f(x)= А или f(x)->A

х->Хо

6.6. Замечательные пределы.

Первым замечательным пределом называется

Lim sinx/x=l

Второй замечательный предел.

6. Экспонента или число е

Число е (число Эйлера, неперово число) играет весьма важную

роль в математическом анализе. График функции y=e^x получил название экспоненты. Широко используются логарифмы по основанию е, называемые натуральными. Натуральные логарифмы обозначаются символом ln

Непрерывность функции

Определение 1. Функция f(x) называется непрерывной в точке

X₀, если она удовлетворяет следующим трем условиям: 1)определена в точке х₀ (т.е. существует f(x₀)

2) имеет конечный предел функции при x –> x₀

3) этот предел равен значению функции в точке x₀, т.е.

Определение 2. Функция у = f(х) называется непрерывной в

точке x₀, если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции:

Свойства функций, непрерывных в точке:

1. Если функции Дх) и ц>(х) непрерывны в точке х₀, то их сумма

произведение и частное

(при условии | являются функциями, непрерывными в точке, х₀.)

Свойства функций, непрерывных на отрезке:

1.Если функция у = f(x) непрерывна на отрезке [а,b], то

она ограничена на этом отрезке

2.Если функция у = f(x) непрерывна на отрезке [а,b], то она достигает на этом отрезке наименьшего значения т и наибольшего значения М (Теорема Вейерштрасса)

3. Если функция у = f(х)непрерывна на отрезке [а,b] и значения ее На концах отрезка f(а) и f(Ь) имеют противоположные знаки, то внутри отрезка найдется точка эпселон £э (а,b) такая, что f(£) = 0 (теорема Больцано-Коши)

Proiz

Определение. Производной функции у = f(x) называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует):

Нахождение производной функции называется дифференцированием этой функции.

Если функция в точке х имеет конечную производную, то функция называется дифференцируемой в этой точке. Функция, дифференцируемая во всех точках промежутка Х₀ называется дифференцируемой на этом промежутке.

Схема вычисления производной. Основные правила дифференцирования

Производная функции может быть найдена по следующей схеме

1°. Дадим аргументу х приращений, найдем наращенное значение функции

2°. Находим приращение функции

3°. Составляем отношение

4°. Находим предел этого отношения при т.е.

(если этот предел существует).

Правила дифференцирования.

1.Производная постоянной равна нулю, т.е.

с'=0.

Правило очевидно, так как любое приращение постоянной функции у=с равно нулю.

2.Производная аргумента равна 1, т.е.

x’=1,при n=1.

В следующих правилах будем полагать, что

дифференцируемые функции.

3.Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же сумме производных этих функций, т.е.

4.Производная произведения двух дифференцируемых функций равна

произведению производной первого сомножителя на второй плюс произведете первого сомножителя на производную второго, т.е.

Следствие 1. Постоянный множитель можно выносить за знак производной:

Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные, например:

5.Производная частного двух дифференцируемых функций может быть найдена по формуле

Производная неявной функции. Выше было рассмотрено дифференцирование явных функций, заданных в виде Рассмотрим дифференцирование неявной функции, заданной уравнением F(x,y)=0

Для нахождения производной функции у, заданной неявно, нужно продифференцировать обе части уравнения, рассматривая у как функцию от х, а затем из полученного уравнения найти производную у '.

Правила Лопиталя.

Это правило в случае дифференцируемости функции позволяет избавляться от неопределённостей типа 0/0 или / при вычисление пределов.

Теорема: Пусть функции f(x) и g(x) дифференцируемы в О(х₀), g’(x₀)0 в О(х₀), f(x₀)=g(x₀)=0 и 

Lim f’(x)/g’(x)=k (конечный или бесконечный предел), тогда  lim f(x)/g(x)=lim f’(x)/g’(x)=k

Замечание(1):f(x₀)=g(x₀)=0 требование можно заменить требованием lim f(x)=0, lim g(x)=0, то есть в т х₀ f(x) и

g(x) могут иметь устранимый разрыв, действительно достаточно переопределить или доопределить f(x) и g(x) по непрерывности, так чтобы f(x₀)=g(x₀)=0

Замечание(2): Если  f’(x₀) и g’(x₀), g’(x₀)0, то утверждение теоремы будет:

lim f(x)/g(x)=lim f’(x)/g’(x)=lim [(x-x₀)(f’(x₀)+(x-x₀))]/ [(x-x₀)(g’(x₀)+ (x-x₀))]=f’(x₀)/g’(x₀)

Теорема: (/) Пусть функции f(x) и g(x) непрерывны в О(х₀), g'(x)0 и О(х₀), дифференцируемы в О(х₀) и

lim f(x)=lim g(x)=;  lim f’(x)/g’(x)=k. Тогда lim f(x)/g(x)=lim f’(x)/g’(x)=k

Замечание: Если функции f’(x) и g’(x) сами удовлетворяют условия теоремы то правило Лопиталя можно применить повторно:

f(x)=e^x g(x)=xⁿ x

lim e^x/xⁿ= lim e^x/1!= nN lim e^x/xⁿ= lim e^x/nx^n-1₌ lim e^x/[n(n-1)x^n-2]=lim e^x/n!=+ f(x)=lnx

x+

g(x)=xⁿ

lim lnx/xⁿ= lim (1/x)/nx^n-1= lim 1/nxⁿ=0

Формулы Тейлора.

Определение: (многочлена Тейлора) Пусть функция y=f(x) – n – раз дифференцируема в точке х₀ многочлен (полином) вида

T_n(х)=f(x₀)+[f’(x₀)(x-x₀)]/1!+ [f’’(x₀)(x-x₀)²]/2!+ [fⁿ(x₀)(x-x₀)]/n! называется многочлен Тейлора с центром в точке х₀ или многочленом по степеням (х-х₀)

Свойства многочлена Тейлора.

Теорема: (основное свойство многочлена Тейлора) Пусть функция y=f(x) – n – раз дифференцируема в точке х₀ f(x)=T_n(x₀); f’(x₀)=T_n’(x₀),…,f⁽ⁿ⁾(x₀)=T_n⁽ⁿ⁾(x₀)