
- •7. Как определяется операция умножения матрицы а на число λ? Приведите пример. Как связаны определители квадратных матриц а и λА размера nxn? Ответ обоснуйте.
- •8. Сформулируйте правило Крамера для решения систем линейных уравнений. Приведите пример применения правила Крамера для системы линейных уравнений от трех переменных.
- •9. Сформулируйте правило Крамера для решения систем линейных уравнений. Докажите правило Крамера для системы линейных уравнений от двух переменных.
- •10. Дайте определение ранга матрицы. Приведите примеры матриц третьего порядка рангов 1, 2 и 3. Что можно сказать об определителе произвольной матрицы размера nxn ранга n? Ответ обоснуйте.
- •17. Докажите что множество решений однородной системы линейных уравнений является линейным пространством. Как найти размерность этого пространства.
- •24. Дайте определение линейного пространства. Приведите примеры линейных пространств, отличных от арифметических пространств Rn.
- •25. Дайте определение базиса линейного пространства. Приведите пример. Докажите однозначность разложения вектора по базису.
- •31. Дайте определение подпространства линейного пространства и приведите пример. Как связаны размерности пространства и его подпространства? Ответ обоснуйте.
- •33. Дайте определение линейного пространства. Докажите, что симметрические матрицы порядка 2 образуют линейное пространство. Найдите его размерность.
- •39. Дайте определение ортонормированной системы векторов.
- •42. Дайте определение скалярного произведения в Rn. Неравенство Коши-Буняковского.
- •44. Дайте определение фундаментального набора решений однородной слау
- •47. Могут ли фундаментальные наборы решений однородной слау различаться а) числом решений? Ответы обосновать.
- •52. Собственные значения и собственные векторы матрицы.
- •63.Матрица линейного оператора.
- •68. Квадратная матрица a называется ортогональной
- •105. Эллипс Эллипс – геометрическое место точек на пл-ти, сумма расстояний от каждой икоторых до 2 заданных точек f1 и f2, называемых фокусами постоянна и равна 2a.
- •106. Гипербола
- •108. Кривые второго порядка.
- •111. Парабола
- •112. Эллипс Эллипс – геометрическое место точек на пл-ти, сумма расстояний от каждой икоторых до 2 заданных точек f1 и f2, называемых фокусами постоянна и равна 2a.
- •117. Выпуклое множество. Выпуклая область
- •125. Сформулируйте основные теоремы двойственности. Как получить решение двойственной задачи из последней симплексной таблицы исходной задачи?
- •122. Какими условиями связаны симметричные взаимно двойственные злп?
1. Укажите, какие из равенств не выполняются для любых матриц А, В, С (предполагается, что все произведения определены): а) АВ = ВА; б) (АВ)С = А(ВС); в) (АВ)Т = ВТ * АТ; г) (АВ)Т = АТ *ВТ. Приведите примеры, опровергающие неверные равенства.
Определение: Матрица – прямоугольная таблица чисел. Отдельные числа (или символы, их заменяющие) называют элементами матрицы.
a11 a12 …a1n
a21 a22 …a2n
…
an1 an2 …ann
mxn – порядок матрицы.
Свойства сложения.
1.Ассоциативность:А+(В+С)=(А+В)+С
2. Коммутативность: А+В=В+А.
3. А+0=А.
Разность матриц: А-В = А+(-1)В
Свойства умножения матриц:
Если матрицы А, В и С таковы, что их произведение возможно, то
1. (АВ)С = А(ВС)
2. А(В+С)=АВ+АС
3. (В+С)А=ВА+СА
4.
![]()
5.
![]() – умножение матриц не обладает свойством
коммутативности.
– умножение матриц не обладает свойством
коммутативности.
Не выполняется АВ=ВА, пример: А – матрица порядка 2х2, В порядка 2х3, в этом случае АВ не равняется ВА, т.к. ВА не существует.
A
=
![]() , B
=
, B
=
![]() ,
,
то
AB
=
![]() , а BA
=
, а BA
=
![]()
Не выполняется АВт = Ат *Вт, пример: А – матрица порядка 2х2, а В порядка 2х3, в этом случае АВт не равняется Ат*Вт, т.к. Ат*Вт не существует.
Остальные равенства выполняются для любых матриц АВС.
3. Дайте определение произведения матриц А и В. Приведите пример, когда АВ существует, а ВА – нет. Существуют ли ненулевые квадратные матрицы А и В такие, что АВ = 0? Ответ обоснуйте.
Пусть
даны матрицы
![]() и
и
![]() .
.
![]() *
*![]() =
=
![]()
Получаем матрицу С, каждый элемент которой равен сумме произведений элементов i–ой строки А на соотв. элемент j–го столбца В.
1)
Произведение А
* В определено,
если s
= m
(число столбцов А
равно числу строк В).
Если
![]() ,
то произведение
,
то произведение
![]() найти
нельзя.
найти
нельзя.
Чтобы оба произведения AB и BA не только были определены, но и имели одинаковый порядок, необходимо и достаточно, чтобы обе матрицы A и B были квадратными матрицами одного и того же порядка.
Например:
А 2 * 3 * В 3 * 4 - сущ. s = m
В
3 * 4
* А 2 * 3
– не сущ.
![]()
2) Если s = m, то матрица произведения A*B имеет порядок r*n.
3) Если произведение матриц определено, то С=АВ есть C=||cik||, где сik = скалярному произведению i строки А на k столбец В.
Существуют ненулевые квадратные матрицы А и В такие, что АВ = 0:
1 2 -2 -2
1 2 1 1
4. Дайте определение произведения матриц А и В. Существуют ли матрицы А и В такие, что АВ = 0, а ВА = Е? Ответ обоснуйте.
Пусть
даны матрицы
![]() и
и
![]() .
.
![]() *
*![]() =
=
![]()
Получаем матрицу С, каждый элемент которой равен сумме произведений элементов i–ой строки А на соотв. элемент j–го столбца В.
1)
Произведение А
* В определено,
если s
= m
(число столбцов А
равно числу строк В).
Если
![]() ,
то произведение
,
то произведение
![]() найти
нельзя.
найти
нельзя.
Чтобы оба произведения AB и BA не только были определены, но и имели одинаковый порядок, необходимо и достаточно, чтобы обе матрицы A и B были квадратными матрицами одного и того же порядка.
2) Если s = m, то матрица произведения A*B имеет порядок r*n.
3) Если произведение матриц определено, то С=АВ есть C=||cik||, где сik = скалярному произведению i строки А на k столбец В.
5. Дайте определения вырожденной и невырожденной квадратных матриц порядка 3. Приведите примеры таких матриц. Докажите, что ортогональная матрица является невырожденной.
Матрица А порядка n*n называется невырожденной, если ее строки линейно независимы, в противном случае – вырожденная.
Теорема: квадратная матрица А невырождена тогда и только тогда, когда ее определитель |А| не равен нулю.
|А|
=
 = -1
= -1
![]() 0 – невырожд.
0 – невырожд.
Квадратная матрица A называется ортогональной, если соответствующая ей система векторов столбцов является ортонормированной.
(ai,aj)=∑k=1nakiakj= δij
Пусть A - ортогональная матрица.
AT=A-1 –необходимое и достаточное условие ортогональности матрицы A.
ATA=E (по определению), A-1A=E.
А т.к. обратная матрица существует, если А невырожденная, то ортогональная матрица является невырожденной.
6. Приведите основные свойства определителей. Проверьте справедливость свойства |АВ|=|А|*|В| для матриц
А=
![]()
![]() и
В=
и
В=
![]()
![]()
Свойства определителей:
1. Если какая-либо строка определителя состоит из нулей, то и сам определитель равен нулю.
2. При перестановке двух строк определитель умножается на -1.
3. Определитель с двумя одинаковыми строками равен нулю.
4. Общий множитель элементов любой строки можно вынести за знак определителя.
5. Если элементы некоторой строки определителя А представлены в виде суммы двух слагаемых, то и сам определитель равен сумме двух определителей Б и Д. В определителе Б указанная строка состоит из первых слагаемых, в Д - из вторых слагаемых. Остальные строки определителей Б и Д - те же, что и в А.
6. Величина определителя не изменится, если к одной из строк прибавить другую строку, умноженную на какое угодно число.
7. Сумма произведений элементов любой строки на алгебраические дополнения к соответствующим элементам другой строки равны 0.
8. Определитель матрицы А равен определителю транспонированной матрицы Ат, т.е. определитель не меняется при транспонировании.
|A| = | 1 2| = 1+2 =3
|-1 1|
|B| = |a b| = ad – bc
|c d|
|A| |B| = 3 (ad – bc)
|AB| = | 1 2| |a b| = |a + 2c b + 2d| =
|-1 1| |c d| |-a + c -b + d|
= (a + 2c)(-b + d) + (a – c)(b + 2d) =
= - ab + ad – 2bc + 2cd + ab + 2ad – bc – 2cd = 3ad – 3bc = 3 (ad – bc)
7. Как определяется операция умножения матрицы а на число λ? Приведите пример. Как связаны определители квадратных матриц а и λА размера nxn? Ответ обоснуйте.
Произведением А на число λ называется матрица, каждый элемент которой равен произведению соответствующего элемента А на λ. Следствие: Общий множитель всех элементов матрицы можно выносить за знак матрицы.
8. Сформулируйте правило Крамера для решения систем линейных уравнений. Приведите пример применения правила Крамера для системы линейных уравнений от трех переменных.
Пусть дана система АХ = В n линейных уравнений с n неизвестными. Если Aне равно 0, то система имеет единственное решение:x1=A1/ A ; x2=A2/ A , где Аi, Определители получаются из определителя|А| заменой соответствующего столбца столбцом свобод членов.
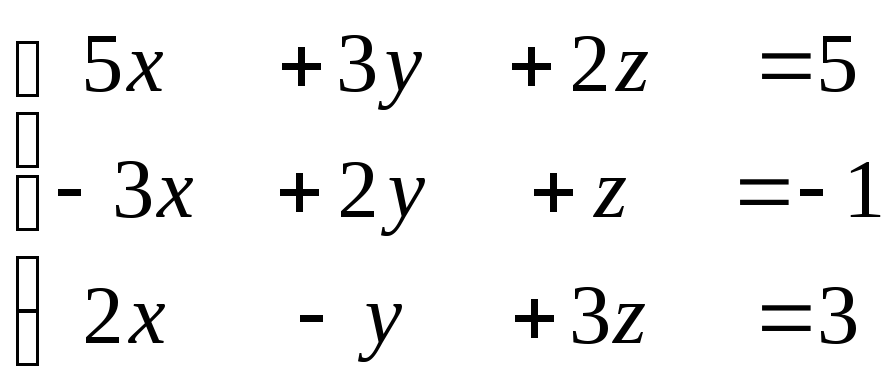
В виде матрицы эту систему можно записать таким образом :
A
=
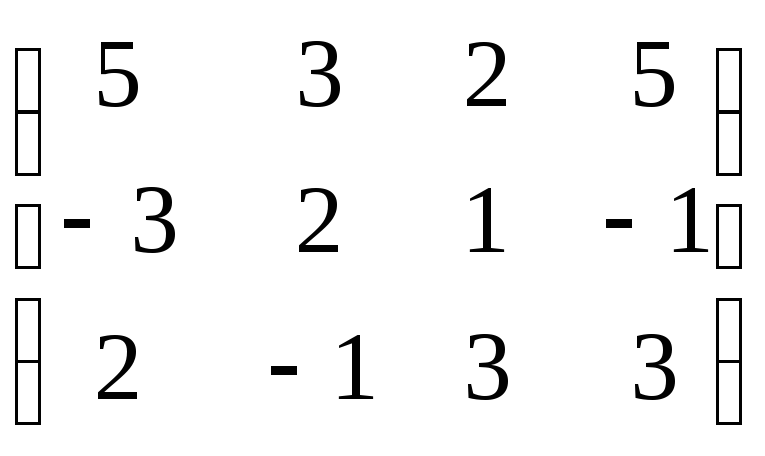 , где
, где
ответы будут уравнений будут находится в последнем столбце. Теперь мы введем понятие основного определителя; в данном случае он будет выглядеть таким образом :
![]() =
=
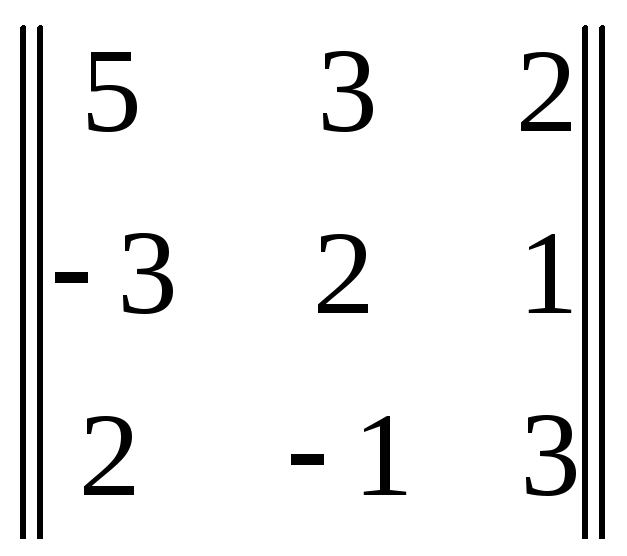 = 66 .
= 66 .
Основным определителем является матрица, составленная из коэффициентов стоящих при переменных. Они также идут в порядке столбцов, т. е. в первом столбце стоят коэффициенты, которые находятся при x, во втором столбце при y, и так далее. Это очень важно, ибо в следующих действиях мы заменяем каждый столбец коэффициентов при переменной на столбец ответов уравнений.
![]() 1
=
1
=
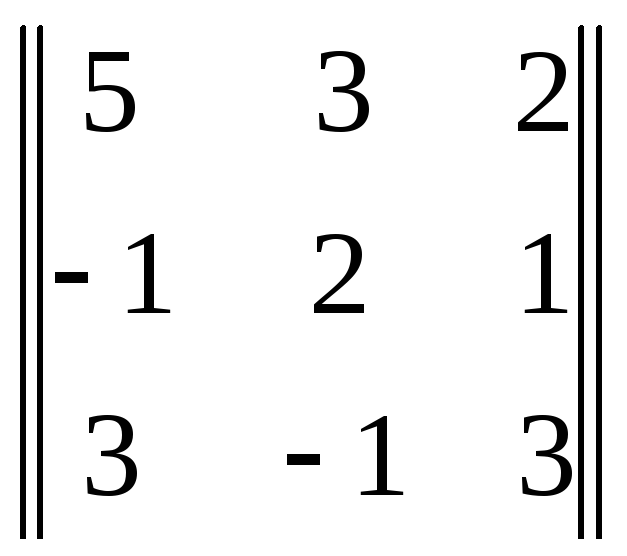 = 43,
= 43,
![]() 2
=
2
= = 41,
= 41,
![]() 3
=
3
=
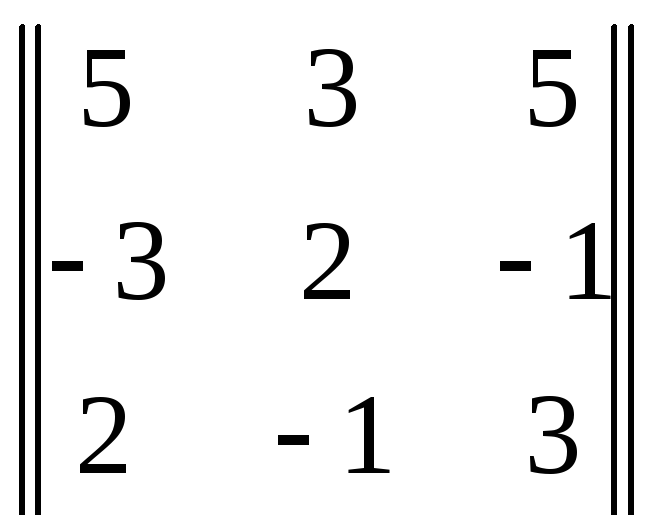 = 51.
= 51.
Затем
нужно найти определители
![]() 1
,
1
,
![]() 2
,
2
,
![]() 3
и применить правило Крамера. Оно выглядит
так :
3
и применить правило Крамера. Оно выглядит
так :
x1
=
![]() =
=
![]() ,
,
x2
=
![]() =
=
![]() ,
,
x3
=![]() =
=![]() – для данного
случая, а в общем виде оно выглядит
следующим образом : xi
=
– для данного
случая, а в общем виде оно выглядит
следующим образом : xi
=
![]() .
.
9. Сформулируйте правило Крамера для решения систем линейных уравнений. Докажите правило Крамера для системы линейных уравнений от двух переменных.
Пусть дана система АХ = В n линейных уравнений с n неизвестными. Если Aне равно 0, то система имеет единственное решение:x1=A1/ A ; x2=A2/ A , где Аi, Определители получаются из определителя|А| заменой соответствующего столбца столбцом свобод членов.
Определители второго порядка (ОВП) имеют вид
![]() =.|a
b|
=.|a
b|
|c d|
Связь ОВП со СЛАУ размерностью 2*2: Представим себе СЛАУ размерностью 2*2 следующего вида
а11*х1+а12*х2=a10
а21*х1+а22*х2=a20
Домножим обе части первого уравнения на a22, а обе части второго уравнения на -a12
а11*а22*х1 + а12*а22*х2 = a10*а22
-а12*а12*х1 + -а12*а22*х2 = -a20*а12
Выражаем неизвестную переменную x1 и получаем:
х1
=
![]()
В числителе и в знаменателе получившейся дроби мы видим вычисленные ОВП.
Проделаем аналогичную процедуру относительно x2.
Значит, для нахождения решения СЛАУ размерностью 2*2 нужно лишь вычислить ОВП составленные из определенных комбинаций коэффициентов при неизвестных и свободных членов и поделить их друг на друга, таким образом, что в числителе дроби ОВП содержащий свободные члены, а в знаменателе соответственно не содержащий.
Пусть
![]() 0.
Тогда СЛАУ имеет единственное решение.
0.
Тогда СЛАУ имеет единственное решение.
Пусть![]() =0,
а
=0,
а
![]() 1=0
и
1=0
и
![]() 2=0.
Тогда СЛАУ имеет бесчисленное множество
решений.
2=0.
Тогда СЛАУ имеет бесчисленное множество
решений.
Пусть
![]() =0,
а хотя бы один из
=0,
а хотя бы один из![]() 1,
1,
![]() 2
неравен 0, тогда СЛАУ не имеет решений.
2
неравен 0, тогда СЛАУ не имеет решений.
