1. Анализ вариации зависимой переменной в регрессии

Рассмотрим вариацию (разброс) значений вокруг среднего значения.

Разобьем эту вариацию на две части: объясненную регрессионным уравнением и не объясненную (т. е. связанную со случайной составляющей ε_t).

Запишем разброс в виде следующего равенства:

И вариация представляется в виде трех слагаемых

Рассмотрим последнее слагаемое. В него входит и тогда

Потому что - по определению, по необходимому условию экстремума

Поэтому верно равенство

,

Где – это TSS, или весь разброс

– это ESS, или необъясненная часть

– это RSS, или объясненная часть

2. Тест Дарбина – Уотсона некоррелированности случайных возмущений в схеме Гаусса – Маркова

Этот тест предназначен для проверки предпосылки о том, что теоремы Гаусса – Маркова, точнее, важнейшего частного случая этой предпосылки, а именно статистической гипотезы

при j=i-1

Неадекватность гипотезы влечет, очевидно, и неадекватность предпосылки. Часто истинной причиной отклонения гипотезы оказывается ошибка в выборе функции регрессии в спецификации модели, например пропуск значимой предопределенной переменной. Эмпирическая корреляция случайных остатков, порожденная этой причиной, называется ложной. Тест Дарбина – Уотсона позволяет идентифицировать, в частности, ложную корреляцию и поэтому рассматривается в эконометрике как один из наиболее важных тестов.

Шаги теста:

1. Модель 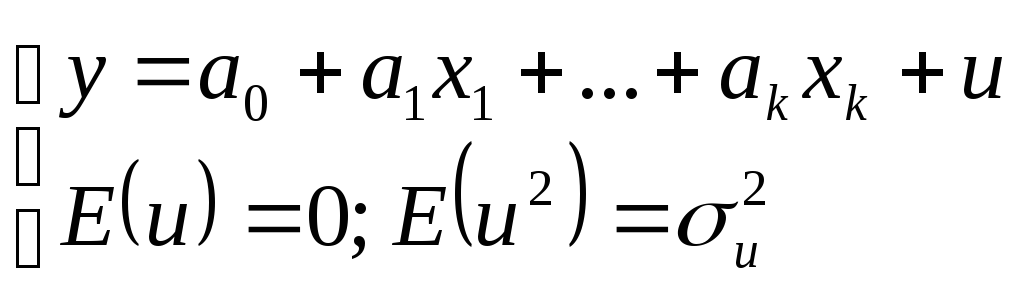оценивается по уравнениям методом наименьших квадратов, рассчитываются по формуле оценки остатков.

2. Для проверки случайной последовательности на корреляцию используется критерий Дарбина-Уотсона 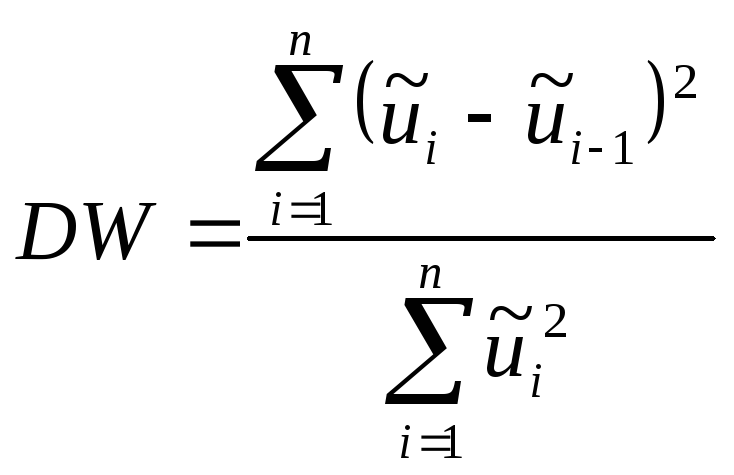Раскроем скобки и проведем преобразование исходной формулы: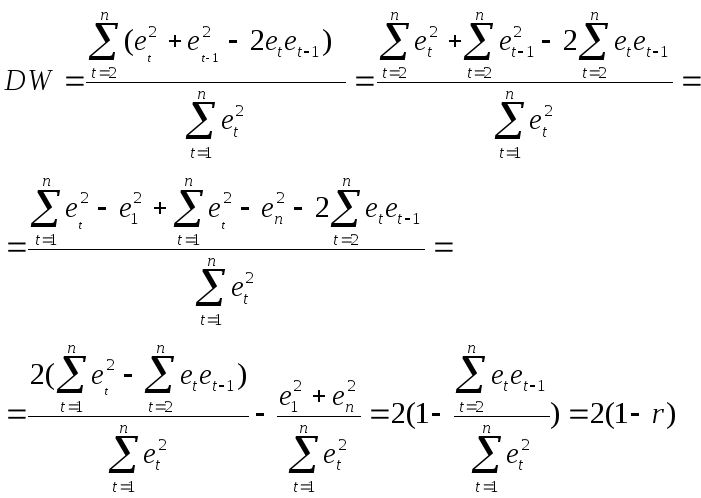

Т.к. 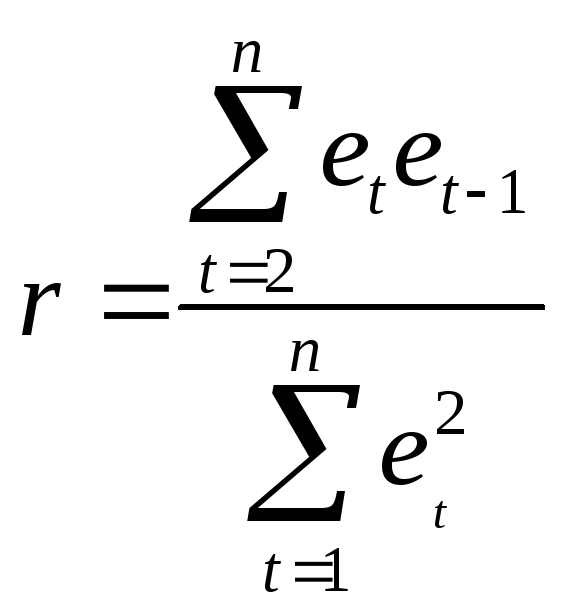r – выборочный коэффициент корреляции

Из полученной формулы следует, что если r =0 (корреляция отсутствует), то DW=2; если корреляция положительна, то DW < 2; если отрицательна - DW > 2. Так как коэффициент корреляции Поскольку критическое значение dкр невозможно табулировать по ряду причин, граница раздвигается и значения левой границы dL и правой границы dU выбираются из таблицы в зависимости от числа наблюдений n, числа независимых переменных k и уровня значимости α. Следовательно, по таблицам Дарбина-Уодсона выбирают 2 константы и , по аргументам 1) 2) 3)

3. Определяется интервал, в который попадает величина DW

Отметим, что тест Дарбина – Уотсона базируется на предположении, что:

1. Функция регрессии модели является неоднородной (параметр 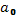подлежит определению)

2. Случайные остатки в уравнениях наблюдений 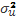распределены по нормальному закону

3. Предпосылки теоремы Гаусса – Маркова справедливы.

3. Метод имитационного моделирования. Исследование последствий нарушения условий теоремы Гаусса – Маркова

Известным методом оценки риска является метод имитационного моделирования (метод Монте-Карло).

Имитационное моделирование, как правило, включает следующие этапы:

1. определение вероятностных распределений каждой переменной;

2. компьютер выбирает случайное значение для каждой неопределенной переменной, основанное на вероятностном распределении этой переменной;

3. отобранное значение вместе с фиксированными факторами (ставкой налогов, амортизационных отчислений и т. д.) используется в модели для определения результативных показателей;

4. этапы 2 и 3 повторяются многократно, например 500 раз. В результате получают распределение 500 значений результативного показателя. Обычно это позволяет вы­делить наиболее вероятное значение.

В каждом эксперименте должна обеспечиваться адекватность условий теоремы Гаусса-Маркова. Величины a₀(j), a₁(j), (j) – несмещённые оценки параметров а₀, а₁, должны быть рассеяна вокруг этих параметров. Разброс оценок относительно параметров должен согласовываться со значениями их средних квадратических ошибок S_a0 и S _a1

Преимуществом метода моделирования является тот факт, что он позволяет увидеть широкий диапазон вероятных результатов, а не несколько дискретных оценок. Тем не менее, метод Монте-Карло мало распространен на практике из-за трудоемкости и сложности выявления всех взаимосвязей и корреляции переменных.

u – случайная переменная (случайный остаток), которая характеризуется своим законом распределения P_u(q).

P_u(q)

Для организации процесса конкретных значений случайной переменной, обладающей законом распределения, существуют таблицы конкретных значений стандартных нормально распределённых случайных переменных.

Эти переменные u₁*, u₂*..u_n*

каждая переменная распределена по нормальному закону распределения. Все переменные являются независимыми в данном наборе. И каждая из них имеет нулевое значение и единичную дисперсию:

Сом (u_i*, u_j*)=0 при i неравном j

E(u_i*)=E(u₂*)= …E(u_n*)=m=0

Var(u_i*)= Var(u₂*)=… Var(u_n*)= =1

Определение значений случайных остатков при нарушении равенства нулю их математического ожидания

Значения u_i(j) определяются по правилу u_i(j)= _i u_i*(j)+m_i, но константы m_i0 при всех i=1,2...n

Полученные значения u_i (j) используются для получения оценочных значений, которые затем оценивают с помощью МНК. Сравниваем полученные оценочные значения a₀ со значением исходного a₀. В случае сильного отличия (больше ошибки) считается, что коэффициент a₀ не обладает свойством несмещенности.

Определение значений случайных остатков при нарушении предпосылки гомоскедантичности

Значения u_i(j) определяются по правилу u_i(j)= _i u_i*(j)+m_i, но величины _iпри всех i=1,2...n

Определение значений случайных остатков и объясняющей переменной при нарушении условия их некоррелированности

Значения u_i(j) определяются по правилу u_i(j)= _i u_i*(j)+m_i, но теперь значения x_i объясняющей переменной модели не могут оставаться в каждом эксперименте j=1,2...N неизвестными. Они должны стать зависимыми от u_i(j). Значение x_i в эксперименте с номером j обозначим x_i (j). Оно будет вычисляться по правилу

x_i (j)= x_i + u_i(j), где x_i значение объясняющей переменной, заданное вне модели.