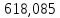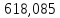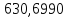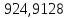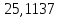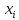ВАРИАНТ	25	Доверительная вероятность для математического ожидания								0,900
		Доверительная вероятность для дисперсии								0,950
		Уровень значимости для метода Пирсона								0,005
-66,5816	-67,3143	-45,3271	-57,7875	-58,5566	-51,4055	-55,1073	-36,2266	-36,8350	-43,5892
-31,4489	-35,8225	-38,6752	-44,6052	-33,0480	-28,7556	-19,9390	-25,6743	-22,2610	-23,3582
-27,6605	-23,6632	-21,3138	-23,2021	-23,5057	-17,8156	-14,9497	-6,0464	-8,8558	-13,7387
-8,3650	-9,3649	-5,9856	-14,9252	-13,8288	4,2611	-1,7182	-0,5471	1,6898	6,1084
6,5337	6,6180	7,3176	12,2487	23,1883	13,2857	12,7587	18,6024	26,5459	42,8212

ЗАДАНИЕ К РАБОТЕ ПО МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕ

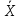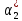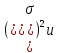
1. Построить вариационный ряд. Найти , , 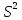для выборки.

2. Разбить вариационный ряд на 10 интервалов и построить:

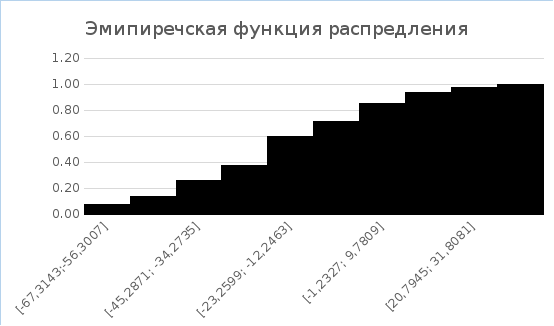
- эмпирический закон распределения выборки;

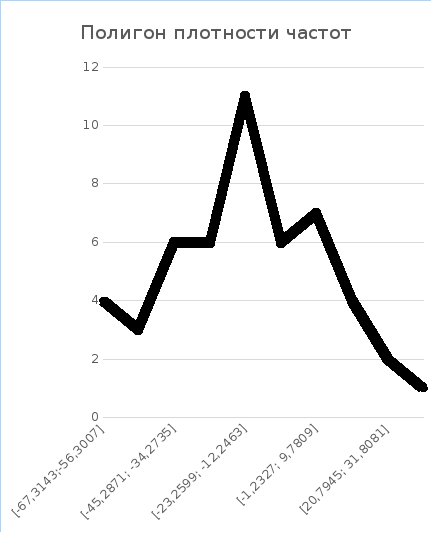
- полигон;

- гистограмму.

3. Выдвигая гипотезу о нормальном характере эмпирического распределения, найти:

- доверительный интервал для математического ожидания α, считая дисперсию неизвестной величиной;

- доверительный интервал для дисперсии 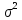, считая математическое ожидание неизвестной величиной.

4. Для заданного уровня значимости проверить гипотезу о нормальном законе распределения по критерию Пирсона.

5. Для заданного уровня значимости проверить гипотезу о равновероятном законе распределения по критерию Пирсона.

1. Решение. Записывая исходные данные в порядке возрастания, составим вариационный ряд:

-67,3143	-66,5816	-58,5566	-57,7875	-55,1073	-51,4055	-45,3271	-44,6052	-43,5892	-38,6752
-36,835	-36,2266	-35,8225	-33,048	-31,4489	-28,7556	-27,6605	-25,6743	-23,6632	-23,5057
-23,3582	-23,2021	-22,261	-21,3138	-19,939	-17,8156	-14,9497	-14,9252	-13,8288	-13,7387
-9,3649	-8,8558	-8,365	-6,0464	-5,9856	-1,7182	-0,5471	1,6898	4,2611	6,1084
6,5337	6,618	7,3176	12,2487	12,7587	13,2857	18,6024	23,1883	26,5459	42,8212

	Выборочное среднее
	Выборочная дисперсия
	Выборочное среднее квадратическое отклонение
	Выборочная исправленная дисперсия
	Начальный эмпирический момент порядка 2
S	Выборочное исправленное среднее квадратическое отклонение

Найдем

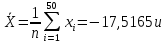
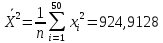
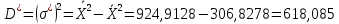
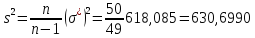
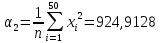
2. Найдем размах, то есть разницу между наибольшим и наименьшим элементами выборки:

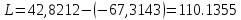
Дальше поделим ряд на 10 равных интервалов. Тогда длинна этих интервалов будет равна:

Составим таблицу

	[-67,3143;-56,3007]	[-56,3007; -45,2871]	[-45,2871; -34,2735]	[-34,2735;-23,2599]	[-23,2599; -12,2463]	[-12,2463; -1,2327]	[-1,2327; 9,7809]	[9,7809; 20,7945]	[20,7945; 31,8081]	[31,8081; 42,8217]
	-61,8075	-50,7939	-39,7803	-28,7667	-17,7531	-6,7395	4,2741	15,2877	26,3013	37,3149
	4	3	6	6	11	6	7	4	2	1
	0,08	0,06	0,12	0,12	0,22	0,12	0,14	0,08	0,04	0,02

Проверим полученные данные

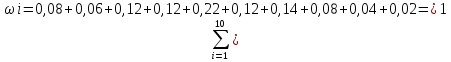
Проверка выполнена успешно.

3. Найдем доверительный интервал для математического ожидания α, считая дисперсию неизвестной величиной

Примем доверительный интервал за

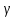
Воспользуемся формулой

Отсюда следует, что уровень значимости будет равен

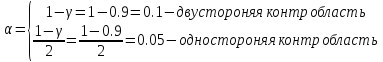
По таблице находим значение t при 0.05 и k=n-1=50-1=49

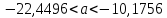
Ответ: (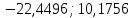) при доверительной вероятности мат ожидании равной 0,900

Доверительный интревал для дисперсии при неизвестном мат. Ожидании имеет вид:

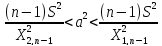
Квантили 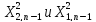найдем по 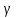найдем из

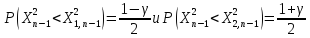
Тогда получим

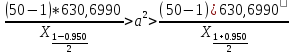
Используем функцию ХИ2ОБР для получение значений

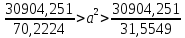
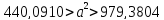
Ответ: () при доверительной вероятности дисперсии равной 0,950