vostrikov

Г л а в а 4

УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ

4.1.ОСНОВНЫЕ ПОНЯТИЯ

Вэтой главе мы начинаем исследование свойств процессов, происходящих в системах автоматики. Важнейшим из них является

устойчивость – основное качественное свойство системы автоматического управления, без которого она неработоспособна.

Физически устойчивость означает, что при ограниченном входном воздействии выходной сигнал также является ограниченным и процессы в системе стремятся к определенным значениям при любых начальных условиях.

Качественный вид переходных характеристик устойчивой и неустойчивой систем изображен на рис. 4.1. Очевидно, что для переходной характеристики устойчивой системы справедливо условие

lim h(t) k.

t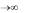

hh

11

kk

2 t t

Рис. 4.1. Переходные характеристики системы:

1 – сходящийся процесс, система устойчива;

2 – расходящийся процесс, система неустойчива

92	Глава 4. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ

Об устойчивости можно судить также по импульсным переходным функциям (рис. 4.2), которые в случае устойчивой системы удовлетворяют условию

lim g(t)	0.
t
g
g
	tt
Рис. 4.2. Импульсная переходная функция
устойчивой системы

Рассмотрим, как можно оценить это свойство для систем, поведение которых описывают уравнения

x Ax Bu, x Rn , u Rm ,

(4.1)

y Cx, y Rm , n m.

Определим зависимость переменных состояния от времени как решение векторно-матричного уравнения состояния (4.1) в виде

t
x(t) eAt x(0) eA(t ) Bu( )d .	(4.2)
0

Здесь первое слагаемое соответствует свободной составляющей движения (из произвольных начальных условий), второе – вынужденной (движение под действием управления).

Одним из основных режимов работы системы управления является

равновесный (статический) режим, при котором переменные со-

стояния с течением времени не меняются, а все производные координат состояния равны нулю.

Покажем, что процесс движения к равновесию можно считать свободным, т. е. он соответствует первому слагаемому в выражении (4.2).

Предварительно запишем уравнение статики, полагая в (4.1) x 0, u const ,

4.1. Основные понятия	93
0 Ax0 Bu,	(4.3)

откуда при det A 0 определим равновесное значение переменных состояния

x0

A 1Bu.

(4.4)

Введем новые координаты, равные отклонениям от точки равновесия,

x x0

(4.5)

и запишем для них дифференциальное уравнение

x

x0

x,

(4.6)

так как x0 0.

После подстановки в (4.6) вместо x его значения из (4.1) с учетом (4.5) получим

A( x0 ) Bu.

Учитывая (4.4), уравнение в отклонениях принимает вид

A .

(4.7)

Как видим, уравнение (4.7) не содержит u, и поэтому переходный процесс по порождается только ненулевыми начальными условиями согласно уравнению

(t) eAt (0).

(4.8)

Линейная система (4.1) называется устойчивой, если для ее про-

цессов выполняется условие

lim (t) 0.

(4.9)

t

Оно представляет собой предел выражения (4.8), которое соответствует первой составляющей решения (4.2). Таким образом, устойчивость линейной системы (4.1) определяется только ее структурой и

94	Глава 4. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ

параметрами и не зависит от величины внешних воздействий и начальных условий. Причем для анализа устойчивости можно не переходить к уравнениям в отклонениях от состояния равновесия, а исследовать свойства матрицы A.

4.2. УСЛОВИЯ УСТОЙЧИВОСТИ ЛИНЕЙНЫХ СИСТЕМ

4.2.1. ОБЩЕЕ УСЛОВИЕ УСТОЙЧИВОСТИ ЛИНЕЙНЫХ СИСТЕМ

Для устойчивости линейной системы (4.1) необходимо и достаточно, чтобы вещественная часть всех собственных значений матрицы A (корней характеристического уравнения) была отрицательной, т. е.

Re( i ) 0, i 1, n.			(4.10)

Покажем справедливость этого утверждения, для чего запишем характеристическое уравнение системы (4.1)

A( p) det( pI	A)		pn a pn 1		a p	a 0	(4.11)
				n	2	1
и найдем его корни i ,	i	1, n . Используя модальное представление,

определим полный процесс в системе, который представляет собой сумму экспонент

	n	it x (0).
x(t)	C e		(4.12)
	i	i
i	1

Как видим, качественный характер переходных процессов полностью определяется значениями корней i .

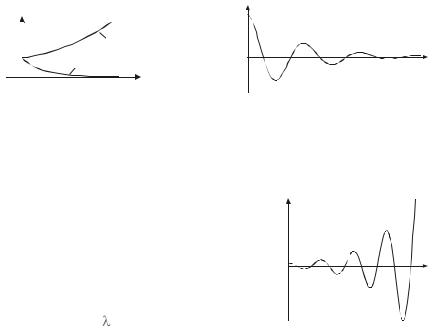
В случае, когда все они вещественные и отрицательные, каждая компонента выражения (4.12) при выполнении условия (4.10) носит затухающий характер (рис. 4.3). Следовательно, и их сумма также будет иметь затухающий характер, т. е. будет с течением времени стремиться к нулю.

4.2. Условия устойчивости линейных систем

95

Если корни характеристического уравнения (4.11) комплексносопряженные с отрицательной вещественной частью, то каждая пара их дает колебательную составляющую процесса, которая мажорируется затухающей экспонентой (рис. 4.4).

			х
			xx
хx	x
	11
	2		t t
	2
			t
		tt
		t
Рис. 4.3. Иллюстрация про-			Рис. 4.4. Колебательная составляю-
цесса в системе с вещест-			щая процесса в случае отрица-
	венным корнем:		тельной вещественной части пары
1 – расходящийся; 2 –		зату-	комплексно-сопряженных корней
	хающий

Следовательно, и в этом случае про-				x
цесс, определяемый соотношением (4.12),
будет иметь затухающий характер.
Таким образом, мы показали доста-
точность условия устойчивости (4.10).
								t	t
Покажем теперь необходимость этого
условия. Предположим, что хотя бы
один из корней	i	имеет положитель-
ную вещественную часть. Соответст-			Рис. 4.5. Процесс в системе
вующая ему составляющая решения бу-			с положительной веществен-
дет с течением времени возрастать и в			ной частью пары комплексно-
пределе стремиться		к бесконечности				сопряженных корней

(рис. 4.5). Следовательно, полный процесс, который определяется выражением (4.12), будет иметь расходя-

щийся характер, а система (4.1) никогда не сможет стать устойчивой. Изобразим корневой портрет системы (рис. 4.6) и получим графи-

ческую интерпретацию условия (4.10): для устойчивости линейной системы необходимо и достаточно, чтобы все корни характеристического уравнения располагались в левой полуплоскости плоскости корней.

96	Глава 4. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ
Im Im
	xx
Re
	t t
Рис. 4.6. Иллюстрация	Рис. 4.7. Процесс в системе с «мнимыми»
корневого портрета	корнями
устойчивой системы

Если хотя бы один корень находится в правой полуплоскости плоскости корней, то система будет неустойчива. Мнимая ось представляет собой границу устойчивости системы: при расположении комплекс- но-сопряженных корней на этой оси система находится на границе устойчивости (при условии, что все остальные корни имеют отрицательную вещественную часть). При этом процессы имеют вид незатухающих колебаний (рис. 4.7).

4.2.2. НЕОБХОДИМОЕ УСЛОВИЕ УСТОЙЧИВОСТИ

Таким условием является положительность всех коэффициентов характеристического уравнения (4.11). В этом можно убедиться, если при известных корнях i представить характеристический полином

A( p) в виде произведения

A( p) ( p 1) ( p n ).

	В случае, когда все корни i , i 1, n , вещественные				i	i ,
i	0	характеристическое уравнение принимает вид

A( p) ( p 1) ( p n ) 0.

Раскрывая скобки, получим уравнение типа (4.11), где все коэффи-

циенты	i	будут положительными. Нетрудно убедиться в том, что

аналогичный результат получится, если корни i комплексно-сопря-

женные с отрицательной вещественной частью.

4.2. Условия устойчивости линейных систем

97

Таким образом, коэффициенты характеристического уравнения (4.11) устойчивой системы всегда будут положительны. При наличии хотя бы одного отрицательного коэффициента система будет неустойчива, дополнительных исследований не требуется.

В то же время следует помнить, что положительность всех коэффициентов характеристического уравнения еще не гарантирует устойчивости системы, необходима ее дополнительная проверка.

ПРИМЕР 4.1

Проверить устойчивость системы первого порядка, передаточная функция которой имеет вид

	k
W ( p)			.
	Tp	1
Ее характеристическое уравнение следующее:
Tp	1	0.
Оно имеет только один корень		1 T , который при T 0 будет ве-

щественным отрицательным.

Следовательно, положительность коэффициентов характеристического уравнения для системы первого порядка является необходимым и достаточным условием устойчивости.

ПРИМЕР 4.2

Проверить устойчивость следующей системы второго порядка:

W ( p)				k				.
	T 2 p2
					2dTp 1
Запишем ее характеристическое уравнение
T 2 p2 2dTp 1						0
и найдем корни
		d			d 2	1	.
1,2		T			T

Они будут иметь отрицательную вещественную часть, если одновременно выполняются условия

T 0, d 0.

98	Глава 4. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ

Таким образом, положительность коэффициентов характеристического уравнения для системы второго порядка также является необходимым и достаточным условием устойчивости.

4.3. КРИТЕРИИ УСТОЙЧИВОСТИ

Применять для анализа устойчивости необходимое и достаточное условие удобно только в случае систем невысокого порядка, полюса которых можно вычислить аналитически. Для проверки устойчивости систем произвольного порядка были разработаны так называемые критерии устойчивости, которые позволяют по характеристическому уравнению или частотной характеристике определить, содержит ли передаточная функция полюса, находящиеся на мнимой оси или в правой половине комплексной плоскости.

4.3.1. КРИТЕРИЙ УСТОЙЧИВОСТИ ГУРВИЦА

Этот критерий сформулирован математиком А. Гурвицем в 1895 г., он является алгебраическим и связывает расположение корней характеристического уравнения с определенными условиями, которые накладываются на его коэффициенты.

Рассмотрим критерий Гурвица без доказательства.

Предварительно из коэффициентов характеристического уравнения

(4.11)

A( p) pn a pn 1	a p a 0
n	2	1

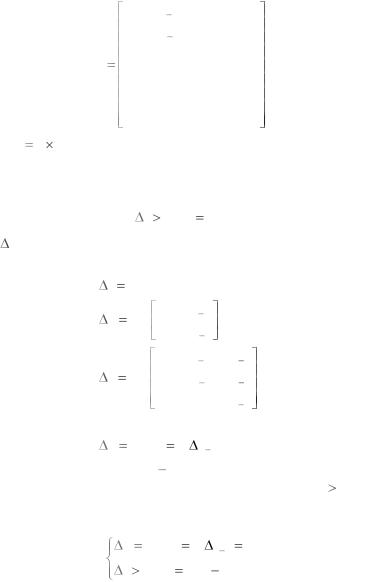
по следующему правилу составляется матрица Гурвица: на главной диагонали сверху вниз выписываются по порядку коэффициенты характеристического уравнения от an до a1 включительно. В каждом

столбце вниз от диагонали записывают коэффициенты при возрастающих степенях оператора p, вверх – при убывающих степенях p. Недостающие элементы в столбце дополняются нулями.

4.3. Критерии устойчивости							99
В результате получим квадратную матрицу вида
	an	an 2		0	0
	1	an 1		0	0
H	0	an		0	0	,	(4.13)
	0	0	a2		0
	0	0	a3		a1

где dim H n n.

Формулировка критерия. Для устойчивости линейной системы необходимо и достаточно, чтобы все n диагональных миноров, полученных из матрицы Гурвица H, были положительны:

i	0, i 1, n.			(4.14)

Здесь i – определители Гурвица, которые составляются следующим образом:

1	an ,
2	det	an	an	2	,
		1	an 1
		an	an	2	an	4
3	det	1	an 1		an	3	,
		0	an		an	2

n det H	a1	n 1.
Поскольку определитель n	1-го	порядка должен быть положи-

тельным, последнее условие соответствует требованию a1 0.

Следствием критерия является условие границы устойчивости, когда последний определитель Гурвица обращается в нуль:

	n det H			a1	n 1		0,
							(4.15)
	i	0, i	1, (n		1).

100	Глава 4. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ

Это условие распадается на два. Одно из них

a1 0,

i 0, i 1,(n 1),

соответствует полюсу, равному нулю. Второй случай условия (4.15) имеет вид

n 1 0,

i 0, i 1, (n 1).

При этом характеристическое уравнение системы содержит два комплексно-сопряженных корня, расположенных на мнимой оси плоскости корней.

На практике критерий Гурвица обычно применяют для проверки устойчивости систем невысокого порядка, так как при высоком порядке условия устойчивости (4.14) становятся очень громоздкими.

ПРИМЕР 4.3

Проверить с помощью критерия Гурвица устойчивость системы третьего порядка, дифференциальное уравнение которой имеет вид

y

a3 y

a2 y a1 y bu.

Запишем ее характеристическое уравнение

p3 a p2	a p	a 0
3	2	1

и составим из коэффициентов матрицу Гурвица

a3 a1 0

H 1 a2 0 . 0 a3 a1

Получим следующие условия устойчивости системы:

1) 1 a3 0;

2) 2 a3a2 a1;

3) 3 det H a1 2 0 или a1 0.