Кошкин Ю.Н. ОТУ / tau_2

	W(p) = x(p) =	T	2	p	2	k	.	(5)
	G(p)					+ T p+1
		1				2
3.1. Переходная характеристика получается при решении уравнения (1), если g(t) = 1 и имеет вид,
показанный на рис.38 для ряда значений ξ =		T2			. Из рисунка видно, что с ростом ξ			колебательность
		2T
			1
переходного процесса уменьшается, исчезая совсем при ξ ≥1.
g(t)	ξ=0,1
x(t)
	ξ=0,4			xуст
	ξ=1
	k	g(t)=1				t
	Рис.38
3.2. Дифференцируя переходную функцию получим импульсную переходную функцию, один из
возможных видов импульсной переходной функции показан на рис.39.

δвых(t)
					δвых(t)
															t
							Рис.39
3.3. Частотная характеристика
3.3.1.								x(jω)								k
							W(jω) =
								G(jω) =				(1− T				2ω 2 ) + jT ω .																			(6)
															1		2
Освобождаясь от мнимой части в знаменателе, получим:
										k(1− T2ω2)										kTω
W( jω) = P(ω) + jQ(ω) =													1			2 2 − j						2										2 .			(7)
									(1	2		2	)	2			(1− T		2		2	)			2	+ T		2
										− T ω					+ T ω				ω										ω
										1						2		1									2
График ЧХ в обычном масштабе при различных ξ имеет вид (рис.40):
Im
																		k(1− T2ω2)
						k										P(ω) =							1										,		(8)
							Re										(1− T		2		2	)		2		+ T		2				2
																			ω										ω
ω=∞							ω=0											1		kT2ω							2
					,5										Q(ω) = −																			,
			0																2		2					2				2			2		(9)
ω3	ξ=						ω1										(1	− T		ω			)				+ T				ω
				5														1											2
		2
		,															k																		T2ω
	0
=						ω2
ξ										A(ω) =																,	ϕ(ω) = −arctg									,
ωi																(1− T2ω2)		2 + T2ω2																	1− T12ω2
		Рис.40														1			2
										ωi	– частота собственных колебаний
3.3.2. ЛАХ:

20lg A= 20lgk − 20lg (1− T12ω 2 )2 + T22ω 2

(10)

при k = 1

20lg A = −20lg(1− T12ω2 )2 + T22ω2 ,

27

20lgA

т.к. ξ = T2

,

то

T = 2ξ T

и

ξ=0,1

40

2T1

2

1

20lg A = −20lg

1+ (4ξ

2 −1)T2ω2

;

30

1

1)

При малых частотах

ξ=0,3

(4ξ2 −1)T2ω2 << 1,

тогда

1

20

20lg A= −20lg1= 0.

2)

При больших частотах

10

(4ξ2 −1)T2ω2 >>1, тогда

ξ=0,4

1

20lg A = −20lgTω

4ξ2 −1.

1

1/T1

10

lgω

1

ξ

3)

В области средних частот

0

=1,

1

1

0

1= (4ξ2 −1)T2ω2

или

ω

=

.

C

T

1

4ξ2 −1

1

-

На

рис.41

приведены

ЛАХ

колебательного

звена.

Она

представляет

4

0

-90°

д

б

собой

ломанную линию, состоящую из двух

/

д

е

к

асимптот, к которым стремится

ЛАХ

при

1,

0

ω → 0 и при ω → ∞. Одна асимптота – ось

−ϕ(ω)

абсцисс при k = 1. В общем случае она идет

вдоль оси абсцисс

на

расстоянии

20lgk .

-180°

Другая асимптота имеет наклон -40 дб/дек.

−ϕ

Рис.41

Точка

пересечения

асимптот

соответствует

частоте ωc = T1 .

1

Если 0,4 < ξ < 0,7, то расхождение между асимптотической и истинными ЛАХ не превышает ±3дб.,

поэтому для таких звеньев можно пользоваться асимптотическими ЛАХ.

При других значениях ξ

асимптотическую ЛАХ корректируют с помощью графиков поправок,

приведенных в литературе (рис.42).

δ, дб

	20							ξ=0,05
	18
	16							ξ=0,10
	14							ξ=0,15
	12
								ξ=0,20
	10
								ξ=0,25
	8
								ξ=0,30
	6
									ξ=0,40
	4
										ξ=0,50
	2										ωΤ
	0
	-2								ξ=0,60
	-4
								ξ=0,80
	-6							ξ=1,0
	-8						1	2	3	4	5 6 7 8 910
	0,2	0,3	0,4	0,5	0,6	0,8 0,9
						Рис.42
Фазовая характеристика имеет при ω → ∞, ϕ →								−π .
4.	Пример: Покажем, что двигатель постоянного тока является колебательным звеном.
						28

ОВД

Uв

U = Eд +iя Rя + Lя

diя

,

(1)

iя

dt

Eд = keω ,

dω

(2)

ω

Mд − MСТ

= J

,

(3)

U

Д

Mд

dt

Mд = kмiя

,

(4)

MСТ

где

U

– входное напряжение якоря двигателя (входной сигнал);

ω– скорость вращения двигателя (выходной сигнал);

ke,kм – постоянные коэффициенты;

J– момент инерции якоря двигателя;

Mд ,MСТ

– момент, развиваемый двигателем и момент сопротивления.

Положим MСТ

= 0. Решив совместно уравнения (1) ÷ (4) относительно U и ω , получим

подставляя (4) в (3)

J

dω

iя

=

kм

dt

и полученный результат в (1), получим

U = k

ω +

JRя

dω

+

JLя

d2ω

,

kм

dt

kм

dt2

e

Разделим левую и правую часть на ke

JL

я

RЯ d2ω

+

JR

я

dω

+ω = kU ,

k

e

k

м

dt2

k

e

k

м

dt

RЯ

1

где k =

– коэффициент передачи двигателя (1/сек).

ke

Обозначим

Lя

= T

;

JRя

= T .

Rя

kekм

я

м

Имеем T T

d2ω

+ T

dω

+ω = kU .

dt2

dt

я м

м

5.Идеальное дифференцирующее звено

1.Звено, выходной сигнал которого пропорционален дифференциалу от входного сигнала называется дифференцирующим звеном:

g(t)	ИДЗ	x(t)

рис. 43

Передаточная функция

	x(t) = k	dg(t)	,	(1)
		dt

k – коэффициент передачи дифференцирующего звена имеет размерность [сек].

Переходим к преобразованию по Лапласу

X(p) = kpG(p).

(2)

		X(p)		(3)
	W(p) =	G(p) = kp.

Уравнение (3) показывает, что порядок оператора p числителя выше порядка знаменателя. Это говорит о том (как уже ранее говорилось), что реально такого звена не существует.

Однако с теоретической точки зрения идеальное дифференцирующее звено представляет интерес.

29

	3.3.1. Переходная функция идеального дифференцирующего звена при g(t) =1, равна x(t) = kδ(t)
	(рис.44), где δ(t) =	d1(t)			– единичная импульсная функция.
			dt
	x(t)				3.2. Импульсная переходная функция будет также δ-функцией (рис.44).
					3.3. Частотная характеристика
	δ(t)
						X(jω)
				t	3.3.1. W(jω) =	G(jω) = jkω		(4)
	Рис.44						Im
	P(ω) = 0;			Q(ω) = kω ;
							ω→∞
				ϕ(ω) = π .
	A(ω) = kω ;						W(jω)
					2		ω→0	Re
	Графически ЧХ в обычном масштабе имеет вид (рис.45)
	3.3.2. ЛАХ:	20lg A(ω) = 20lgk +20lgω					Рис.45
	при k =1			20lg A(ω) = 20lgω
	20lgA				+20 дб/дек	Наклон ЛАХ соответствует +20 дб на декаду
						(почему?) (рис.46).
					ϕ	При k ≠1 ЛАХ перемещается параллельно
	+90°					самой себе по оси ординат на величину 20lgk .
					lgω	ЛФХ:	ϕ(ω) = π2 .
	–ϕ				Рис.46
	4. Пример:

			iвых		при	R = 0;
					iвых	= C	Uвх	;
Uвх				С			dt

6. Реальное дифференцирующее звено

Как было указано выше, реализовать идеальное дифференцирующее звено практически невозможно. Оно реализуется только при наличии дополнительных помех, т.е. звеном, обладающим конечной инерционностью.

1. Такое звено описывается уравнением:

g(t)

x(t)

dx(t)

dg(t)

РДЗ

T dt

+ x(t) = k

dt ,

(1)

2. Преобразование Лапласа:

рис. 47

(Tp +1)X(p) = kpG(p).

(2)

Передаточная функция

X(p)

kp

W(p) =

(3)

G(p) = Tp +1.

30

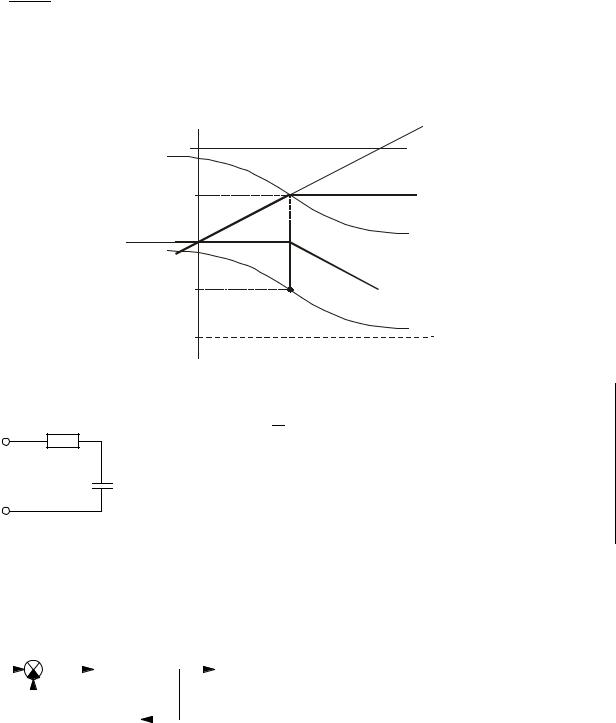
Реальное дифференцирующее звено (3) уже нельзя считать типовым, т.к. его можно заменить последовательным соединением идеального дифференцирующего звена W1(p) = kp и апериодического

1

W2 (p) = Tp +1.

3.1.проанализировать самостоятельно;

3.2.проанализировать самостоятельно;

3.3.1.проанализировать самостоятельно;

3.3.2. ЛАХ: 20lg A(ω) = 20lg		kp		+ 20lg	1	.
					Tp +1

4. Пример:

R

iвых

Uвх С

20lgA

+90°

+45°

0

1

=

и

k

р

п

,

p

k

lg

0

2

ϕ

−

.

р

е

к

з

е

у

/д

л

ь

ти

б

д

0

1

+2

	ϕидз
20lg W(jω)
рующая	2	lgω

-45°

-90° -ϕ°

Uвх = iвых

ω=1/Τ		20
		-		д
				б
				/
				д
				е
				к.

ϕ	20lg (1/Tp+1)
АЗ

Рис.48

1 T

R + C ∫0 iвыхdt ,

T

CUвх − CRiвых = ∫iвыхdt ,

0
T	diвых	+iвых = kUвх ,	T = RC; k = C .
	dt

Охват апериодического звена обратными связями

1. Охват ООС.

Запишем уравнения:

G(p)

ε

k

X(p)

(p)

ε(p) = G(p) − X1(p),

Tp+1

k

X1(p)

X(p) =ε(p)

,

(1)

koc

Tp +

1

X1(p) = X(p)koc .

рис. 49

Решаем (1) совместно относительно G(p)

и X(p), получим

: (1+kkoc )

k

W(p) =

X(p)

=

k

=

1+ kkoc

G(p)

Tp + (1+ kkoc): (1+kkoc )

T

p +1

1+ kkoc

или обозначив

31

k

=

k

,

T =

T

, получим W(p) =

k1

.

1+ kk

1+ kk

T p+1

1

oc

1

oc

1

Таким образом при охвате апериодического звена ООС, получим также апериодическое звено, однако, уменьшается коэффициент усиления (передачи) этого звена в установившемся режиме, и увеличивается быстродействие звена, т.к. уменьшается его постоянная времени.

2. Охват ПОС.

Проделывая аналогичные выкладки, получим:

G(p)

ε

k

X(p)

(p)

k1

Tp+1

W(p) =

,

X1(p)

T p+

1

koc

k

1

T

где

k

1

=

и T

=

.

рис. 50

1− kkoc

1

1

− kkoc

2.1.

Если kk

>1, то

характеристическое

уравнение

Tλ +1= 0,

T

λ +1= 0, где

oc

1

1− kkoc

λ = −1−Tkkoc , имеет положительный вещественный корень, следовательно имеем расходящийся

(неустойчивый) процесс.

2.2.Если kkoc < 1, то корень характеристического уравнения отрицателен, следовательно

полученное апериодическое звено остается устойчивым. При этом возрастает как коэффициент усиления (передачи) звена, так и его постоянная времени, т.е. быстродействие звена уменьшается.

Структурные преобразования

В результате разбиения САУ на типовые звенья направленного действия и получения их передаточных функций, составляется структурная схема всей системы.

Структурная схема – это диаграмма прохождения сигналов управления и их преобразования в САУ. Структурная схема – это математическая модель системы.

Структурные схемы для реальных САУ имеют сложный и запутанный вид. С целью упрощения структурной схемы или приведения ее к более удобному виду, можно производить структурные преобразования по определенным правилам:

Правила преобразования структурных схем

1. Преобразование последовательного соединенных звеньев.

x1(p)

x2(p)

x3(p)

x1(p)

?

x3(p)

x

2 (p) = x1(p)W1(p),

W1(p)

W2(p)

W2(p)

(1)

x

3

(p)

= x

2

(p)W

2

(p).

рис. 51

Решая

(1)

совместно,

получим

x3(p) = x1(p) W1(p)W2 (p) или передаточная функция двух последовательно соединенных звеньев

W(p) =

x3(p)

= W

(p)W

(p).

(2)

x (p)

1

2

1

Итак,

при n последовательно соединённых звеньев с передаточными функциями Wi (p) (i =

),

1,n

результирующая передаточная функция равна

произведению

передаточных

функций

отдельных

n

звеньев:

W(p) = ∏Wi (p)

i=1

32

2. Преобразование параллельного соединенных звеньев.

W1(p)	x2(p)
x1(p)	x4(p)
W2(p)	x3(p)
	рис. 52

Решая (1) совместно, получим

					?			x2	(p) = x1(p)W1		(p),
						x4(p)		x3	(p) = x1(p)W2		(p),		(1)
				x1(p)	W(p)
								x4	(p) = x2 (p) + x3 (p).					)
x	4		(p) = x (p)W (p)+ x (p)W (p) = x (p) W (p)+W (p)
			1		1	1		2	1	( 1		2

или

W(p) =

x4 (p)

= W (p) +W (p).

x1(p)

1

2

Таким

образом,

передаточная функция n

параллельно

соединенных звеньев

равна

сумме

n

передаточных функций отдельных звеньев:

W(p) = ∑Wi (p).

3. Звено, охваченное обратной связью:

i=1

3.1. ООС.

?

x1(p)

x2(p)

x3(p)

x1(p)

x (p)

x2

(p) = x1(p) − x4

(p),

W1(p)

W(p)

3

x3 (p) = x2 (p)W1(p),

(1)

x4(p)

x4 (p) = x3 (p)Woc (p).

Woc(p)

рис. 53

Решая (1) относительно x3(p) и x1(p), получим:

W(p) =

x3(p)

=

W1(p)

;

x (p)

1

+W (p)W (p)

1

1

oc

3.2. ПОС. Проводя аналогичные рассуждения, получим:

W(p) =

W1(p)

;

1−W (p)W (p)

1

oc

3.3. Частный случай: при единичной ОС.

x1(p)

x2(p)

x3(p)

x1(p)

?

x3(p)

W (p)

W1(p)

W(p)

W(p) =

1

.

1±W (p)

+

–

1

Причём знак ”+” соответствует

рис. 54

ООС.

Знак ”–” соответствует ПОС.

Пример:

	x1(p)		x2(p)			x3(p)
					W1(p)=k1/p

W2(p)=k2

рис. 55

1 1

обозначив k = k2 и T = k1k2 , получим

W1(p)

k1

W3

(p) =

=

p

=

1

+W

(p)W

(p)

+

k1k2

1

1

2

1

=

k1

:k1k2

=

k2

,

p + k1k2 :k1k2

1

p +1

k1k2

W (p) =

k

;

3

Tp+1

33

Таким образом, интегрирующее звено, охваченное безынерционной обратной связью, эквивалентно типовому апериодическому звену, т.е. уже не является интегрирующим.

Правила переноса сигнала

В общем случае структурные схемы могут иметь различного рода перекрещивающиеся связи, поэтому для приведения структуры к одноконтурной – удобной для исследования, разработаны правила переноса сигналов из одной точки структуры в другую:

1. При прямом переносе сигнала через ПФ W1:

x1(p) W1(p) x2(p)

x1(p) x2(p)= x1(p)W1(p).

рис. 56 2. При обратном переносе сигнала через ПФ W1:

	x1(p)		x2(p)
		W1(p)
					x2(p)= x1(p)W1(p).
				x2(p)

рис. 57 3. При прямом переносе суммирующего звена:

		x2(p)				x4(p)
x1(p)			x3(p)
					W1(p)
	x4(p)= (x1(p) – x2(p)) W1(p).							рис. 58

4. При обратном переносе суммирующего звена:

x3(p)

x1(p)			W1(p)		x2(p)

x1(p)= x2(p) 1/ W1(p). 1/W1(p)

x1(p)

x1(p)

x2(p)

W1(p)

x1(p)

W1(p)

x2(p)

x2(p)

W1(p)

x1(p)

x4(p)

W1(p)

x4(p)= x1(p) W1(p) – x2(p) W1(p).

x3(p)

1 W1(p)

x1(p)

x2(p)

x4(p)

x1(p)

x4(p)

W1(p)

рис. 59

W1(p)

x4(p)= x1(p)W1(p) – x3(p).

x4(p)=[x1(p) – x3(p)/W1(p)] W1(p).

5.

x2(p)

x3(p)

x1(p) +

– x3(p)

x1(p)

+

–

–

x3(p) = x1(p) ± x2 (p).

x2(p)

+

x1(p)

рис. 60

x1(p) = x3(p) µ x2 (p).

6.

34

x1(p)		x3(p)			x1(p)					x3(p)
+		–					+			–
x2(p)			+
							–
x3(p)= x1(p) ± x2(p).
					x3(p)
			рис. 61

Замечание: 1) Структурные преобразования можно производить только в том случае, если анализ динамической системы производится при нулевых начальных условиях. В противном случае структурные преобразования приводят к потере начальных условий и погрешностям при дальнейшем анализе.

2) Структурные преобразования лишены физического смысла.

Передаточные функции систем по управляющему и возмущающему воздействиям

				F(p)
G(p)	E(p)	x1(p)	x2(p)	x3(p)	W3(p)	x(p)
		W1(p)	W2(p)
			рис. 62
	E(p)	– изображение ошибки системы;
	G(p)	– управляющий сигнал;
	F(p)	– возмущение.

Запишем уравнения по структуре (рис.62)

E(p) = G(p) − x(p),

x1(p) = E(p) W1(p), x2 (p) = x1(p) W2 (p), x3 (p) = x2 (p) − F(p),

x(p) = x (p) W (p).

3 3

Решая систему (1) относительно x(p),

G(p) и F(p), получим

W1(p) W2 (p) W3 (p)

W3 (p)

F(p).

x(p) =

G(p) −

1+W

(p) W

(p) W (p)

1+W

(p) W

(p) W (p)

Обозначим

1

2

3

1

2

3

W1(p) W2 (p) W3(p)

W (p) =

– передаточная функция по управлению.

y

1

+W1(p) W2 (p) W3(p)

(1)

(2)

	WF (p) =			W3(p)		– передаточная функция по возмущающему воздействию.
		1		+W1(p) W2 (p) W3	(p)
	W1(p) W2 (p) W3(p) =Wp (p)				– есть передаточная функция разомкнутой системы. Чтобы

получить её необходимо мысленно разорвать контур обратной связи (волнистые линии на рис.62) и место разрыва считать одновременно входом и выходом системы.

	Wp (p)		W (p)
x(p) =		G(p) −	3	F(p).
	1+Wp (p)		1+Wp (p)

35

При совместном действии на систему G(p) и F(p) исследование ведется отдельно по каждому

воздействию. Суммарный результат получается алгебраическим сложением всех результатов. Это справедливо лишь для линейных систем.

При исследовании систем стабилизации в качестве исходной служит передаточная функция WF (p) по возмущению, тогда структура преобразуется к виду (рис.63).

F(p)	X(p)
	W3(p)

x2(p)

W1(p)W2(p)

рис. 63

Если анализируется следящая система, то за исходную принимается ПФ Wy (p) по управлению при

F(p) = 0 (рис.64).

G(p)	X(p)
	W1(p)W2(p)W3(p)

рис. 64

Для того, чтобы получить характеристическое уравнение системы достаточно приравнять нулю знаменатель ПФ замкнутой системы.

Проблема устойчивости в САУ

Устойчивость – это свойство системы возвращаться в исходный или близкий к нему установившийся режим после всякого выхода из него в результате какого-либо воздействия.

Пример:

1)

2)

устойчивое	неустойчивое
3)	4)

устойчивое в малом	полуустойчивое
и неустойчивое в большом

Рис.65

Устойчивость является важнейшим качественным свойством систем управления. Любая САУ создается таким образом, чтобы её основной режим работы был устойчивым.

Рассмотрим линейную САУ, которая описывается системой дифференциальных уравнений:

&	n	, u R	m	.	(1)
x = Ax+ Bu, x R

Основным режимом её работы является статический режим или состояние равновесия, когда

&	(2)
x = 0.

Решая (1) с учетом (2)

36