Добавил:

borisow03 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Новосибирский государственный технический университет

Предмет:

Основы Теории Управления

Файл:

Кошкин Ю.Н. ОТУ / tau_4

.pdf

Скачиваний:

Добавлен:

23.01.2019

Размер:

807.35 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

2. Имеем одномерную САУ, описываемую системой дифференциальных уравнений:

	&	= xi+1,
xi
	&	n
		= ∑aj xj + Bu,
xn
		j=1

i =1,(n−1), u R1.

Т.к. u нет в первых (n − 1) уравнениях, то желаемую динамику можно задать только для n-го уравнения, в которое входит u в виде

&
&	= xi+1	, i	=1,(n−1),
xi	= xi+1	, i	=1,(n−1),
F(x,v) = &	= Fn (x,v).
xn	= Fn (x,v).
Координаты x1 , Κ		xn−1	будут изменяться в соответствии с изменениями координаты xn .

Модальный метод синтеза

Данный метод относится к методам синтеза многомерных и одномерных систем с использованием их модальных характеристик (собственные числа или корни характеристического уравнения, собственные вектора).

Постановка задачи

1. Имеется модель объекта в виде

(1)

R .

x = Ax + Bu, x R , u

2. Заданы требования к замкнутой системе в виде желаемого расположения корней.

Λ* = {λ1* ,λ2* , Κ , λn*},

которые определяются по требованиям, предъявляемым к САУ:

tp ≤ tp.зад.

– время регулирования;

µ ≤ µзад.

– колебательность;

σ% ≤σзад. % – перерегулирование.

По ним вычисляется сектор (рис.111)

≈

, r ≈

µ = max

ωi

r = min

αi

В данном заштрихованном секторе корни выбираются произвольно, тогда ПП в системе будут удовлетворять заданным требованиям.

На практике корни необходимо выбирать ближе друг к другу и к границе сектора. При этом упрощается структура регулятора.

Расположение	Re
желаемых
корней системы
	r

Рис.111

Управляющее воздействие системы формируется в виде отрицательной обратной связи
u = k(x − v),	(2)

где v – вектор входных воздействий на систему, v Rm ;

k – матрица коэффициентов усиления, значения которой необходимо найти в процессе синтеза dimk = n × m.

Подставим (2) при v = 0 в (1), получим

x = Ax + Bkx = (A + Bk)x .	(3)
&	(3)
Характеристическое уравнение (3) будет:
det[λI − A − Bk]= 0.	(4)
Решая (4) определяем совокупность корней замкнутой САУ – Λ(k). Так как матрицы	A и B
постоянны и известны, то корни являются функциями элементов матрицы k .
Приравниваем	(5)
Λ(k) = Λ* – желаемым	(5)

и из (5) определяем матрицу k .

Соотношение (5) лежит в основе модального метода синтеза.

Трудности из линейной алгебры:

1. Т.к. dimk = n × m, а уравнений (5) равно n, то nm− n = n(m− 1) – величинам k необходимо

придать произвольные значения, а остальные n величин k определяются из уравнений (5);

2. Обычно Λ(k) – сложная нелинейная зависимость, что затрудняет непосредственное определение

матрицы k по основному соотношению (5);

3. Аналитически определить корни замкнутой системы Λ(k) можно лишь для n≤ 5.

Поэтому практически при синтезе основное соотношение (5) не используется. От корней переходят к коэффициентам характеристического уравнения (4), т.к. между ними существует взаимно-однозначное соответствие. Тогда процедура расчета будет следующая.

Известно:

&	+ Bu,
x = Ax
	при v = 0.
u = kx,

Задаемся из показателей качества желаемыми корнями

Λ* = {λ1* ,λ2* , Κ , λn*}.

Требуется определить матрицу k = ? dimk = n × m. Определяется характеристическое уравнение САУ:

det[λI − A − Bk]= λn + Cn (k)λn−1 + Cn−1(k)λn−2 +Κ + C2 (k)λ + C1(k) = 0.

По заданным показателям качества ПП определяется желаемое характеристическое уравнение

λn + Cn*λn−1 + Cn*−1λn−2 +Κ + C2*λ + C1* = 0.

(1)

(2)

(3)

(4)

Далее приравниваем коэффициенты (3) и (4) при одинаковых степенях λ , т.е.	(5)
Ci* = Ci (k), i = 1,n.

Соотношение (5) является основным расчетным соотношением для систем любого порядка.

Снова имеем n × m – неизвестных составляющих матрицы k и n уравнений (5), следовательно n(m− 1)- значений k задаются произвольно, а остальные вычисляются из уравнений. Т.е. вычисление

по соотношению (5) свойственны те же сложности, о которых ранее было сказано для корней.

Поэтому для упрощения процедуры синтеза используют преобразование координат, которое позволяет получить каноническую форму уравнений состояния объекта.

Каноническая форма – это такие уравнения объекта, которые имеют минимальное число ненулевых элементов.

Преобразование от произвольной формы к канонической называют каноническим преобразованием.

Канонические преобразования

Рассмотрим канонические преобразования на примере скалярного объекта:

+ Bu, x R

, u R

= Ax

Первая каноническая форма

Утверждение: Если объект управляем,

то

существует

такое невырожденное преобразование

координат x~ = T x, detT ≠ 0, что уравнение объекта может быть представлено в

виде 1-й канонической формы:

x =

+ Bu,

− a

[I]

− a1

где A

Λ 2

B =

n−1

− an

I – единичная диагональная матрица, размерности (n − 1) .

Матрица B имеет один коэффициент ≠ 0, все остальные элементы =0.

ai (i =1,n) – коэффициенты характеристического уравнения det(λI − A) = 0,

представленного в виде

λn + anλn−1 + an−1λn−2 +Κ + a2λ + a1 = 0.

В качестве матрицы T1 выбирается матрица

T1 = P−1 = [B AB A2B Κ An−1B]−1 .

Пример:

x = Ax + Bu,

где A =

−1

B =

5 ,

1 ,

det(λI − A) =

λ − 1

= λ

− 6λ + 7

= 0 – характеристическое уравнение объекта.

−

λ − 5

Составим матрицу управляемости:

P =[B

тогда

AB]= 1

−

−1 =

T = P−1

−

det

−

т.к. det P = 18− 1= 17

x = T

−1

x = T x

, подставляя в исходное уравнение:

−1~&1

−1~

+ Bu

−1 ~

+ T1Bu

T1 x = AT1 x

x = T1

AT1

x = Ax

1 2~

+ ~

Bu,

			9	−		1						−	119
~								1	− 1 2	1	0			0	− 7
~		17					17	1	− 1 2	1	0		17	0	− 7	,
A	=		1			2		2	5 1	9	=	102		= 1	6	,

													17
	− 17				17						1		17
			9	−		1
~								2	1
~		17				17		2	1
B	=		1			2		1	= 0 .
	−
	−		17	17
			17	17

Вторая каноническая форма

Утверждение: Если

объект

управляем,

то

существует

такое невырожденное

преобразование

координат

= T2 x, detT2

≠ 0, что уравнение объекта может быть представлено в

виде 2-й канонической формы

[I]n−1

x =

x +

− a

Μu

det(λI − A) = 0,

где

–

коэффициенты

характеристического уравнения

представленного в виде

λn + anλn−1 + an−1λn−2 +Κ + a2λ + a1 = 0.

В качестве матрицы T2 используется матрица преобразования вида

T2 = M−1 P−1

где M – вспомогательная матрица, составленная из коэффициентов характеристического уравнения объекта, матрица M – треугольная и имеет вид:

	a2		a3	Λ	an	1
	a3			Λ	1	0
		Μ	Μ
M =		Μ	Μ		Μ Μ
M =			1	Λ	0
	an		1	Λ	0	0
		1	0	Λ	0	0

Рассмотрим предыдущий численный пример:

Пример:

det(λI − A) = λ2 − 6λ + 7 = 0 – характеристическое уравнение Составим матрицу M :

																										M =				− 6				1
																										M =				1				0 .

Найдем матрицу M−1 :																													1					0	−1
																								M	−1	=			1					0	−1	,
																								M		=		det				−1			− 6	,
																												det			M
т.к.			det M = −1							,	то	M	−1		=	0			1				,
т.к.			det M = −1							,	то	M			=	1			6				,
~											−1~														−1 ~
~		= T2 x x									−1~					~&									−1 ~
x		= T2 x x								= T2		x					x		= T2					AT2		x + T2 Bu ,
																					14 2~43							{~
																								A					B
															9			−			1					1				2
										0		1												=	−
T		= M−1 P−1 =								0		1		17							17			=	−		17			17			,
2										1		6			1						2					3				11
													−
													−		17											17
															17				17							17				17
T	−1		= (M−1 P−1)−1 = PM =													2				1			− 6			1		=	−11					2	,
2																1			9				1			0					3 1

				1			2																			0				1
~			−								1	−1 −11 2																							0	1
~			−			17			17		1	−1 −11 2																							0	1
A		=		3			11				2	5				3						1		= −		119				102				= − 7		6	,
A		=		3			11				2	5				3						1		= −										= − 7		6	,

				17			17																			17					17
				17			17
				1			2
~			−								2		0
~			−		17			17			2	=	0
B		=		3			11				1	=	1 .

				17			17
				17			17

Синтез скалярных систем модальным методом

Исходная САУ описывается системой уравнений:

&	+ Bu,
x = Ax	+ Bu,			(1)
		(u,y,v) R1	, x Rn .	(1)
y = Cx,		(u,y,v) R1	, x Rn .

u = kx + Dv,
Матрицы A,B,C любого вида. k =[k1,k2,		Κ ,kn ] – коэффициент усиления регулятора.

Для системы (1) необходимо определить параметры регулятора, обеспечивающего в замкнутой

системе	желаемое	распределение	корней			λ* ,λ*			, Κ , λ* ,	которые	соответствуют желаемому
характеристическому уравнению:							1	2	n
характеристическому уравнению:											(2)
		λn + Cn λn−1 + Cn−1λn−2 +Κ + C2 λ + C1								= 0.	(2)
От произвольного описания объекта (1) перейдем, с помощью невырожденного преобразования T2
ко второй канонической форме: x~ = T x,				detT		≠ 0.
Тогда			2		2
Тогда			~&		~~			~			(3)
			~&		~~			~			(3)
			x = Ax			+ Bu,
	~ 0	[I]		~		0
где	A = Λ	n−1		,	B =
где	A = Λ			,	B =		Μ.
		− a2 Λ	− an
	− a1	− a2 Λ	− an			1

Если v =

то

u = kx

u = kT

−1

x , обозначим

k~ = kT

, k~ =[k~

,k~

−1

, Κ , k~ ].

Подставим u в (3)

~~ ~

x = (A

Bk )x .

Характеристическое уравнение (4)

det(λI −

− Bk ) = 0,

n−1

n−2

+ (an − kn )λ

+ (an−1

− kn−1 )λ

+Κ + (a2

− k2 )λ + (a1

− k1 ) = 0.

(4)

(5)

Приравнивая между собой коэффициенты (5) и желаемого характеристического уравнения при одинаковых степенях λ , получим

~ ~			(6)

Ci = ai − ki , i =1,n.

Как видно из (6) при определении коэффициентов регулятора для канонической формы достаточно определить коэффициенты характеристического уравнения замкнутой системы и коэффициенты желаемого характеристического уравнения.

Из (6)

~	~		(7)
~	~	− Ci , i =1,n.	(7)
ki	= ai	− Ci , i =1,n.
От k~i перейдем к реальным k		~	(8)
		~
		k = kT2 .

Итак: Алгоритм синтеза модальным методом.

1.По дифференциальным уравнениям объекта находится характеристическое уравнение.

2.По заданным показателям качества определяется желаемое характеристическое уравнение замкнутой системы.

3.Выбирается управляющее воздействие в виде обратной связи по состоянию в виде u = kx.

4.Вычисляется матрица преобразования T2 .

	~	~
5.	~	~	− Ci , i =1,n вычисляются коэффициенты преобразованной
5.	По уравнению (7) ki	= ai	− Ci , i =1,n вычисляются коэффициенты преобразованной
	матрицы регулятора.		~
6.			~
6.	Определяются элементы матрицы коэффициента регулятора по выражению (8) k = kT2 .

Пример:

Рассмотрим тот же пример, где

1	−1	2	k = ?
A = 2	5 ;	B = 1 ;	k = ?

1. Характеристическое уравнение объекта det(λI − A) = 0			→ λ2 − 6λ + 7 = 0.

2.Пусть λ1* = −1; λ*2 = −2.

Желаемое характеристическое уравнение замкнутой системы будет

(λ − λ1* )(λ − λ2* ) = (λ +1)(λ + 2) = λ2 + 3λ + 2 = 0. 3. Выбираем управляющее воздействие u = kx = k1x1 + k2x2 .

				1	2
		−
4. Вычисляем матрицу T	=	−		17	17		.
4. Вычисляем матрицу T	=			17	17		.
2				3	11

			17
			17			17

	~		~	−C = 7−	2 =	5,
	k	1	= a
5.			1	1
	~		~	−C2 = −6−3 = −9.
	k	2	= a2

				1	2
~		−						32		89
~		−						32		89
6. k =[k1 k2 ]= kT2	=[5	− 9]		17	17		= −		−		.
6. k =[k1 k2 ]= kT2	=[5	− 9]		17	17		= −		−		.
				3		11		17		17
			17		17

Статический расчет системы

Кроме требований к динамике в замкнутой САУ требуется обеспечить заданные статические свойства. В частности, требуется, чтобы по окончании ПП выходная координата соответствовала бы заданной, т.е. необходимо

lim y(t) = v,	(1’)
t→∞
где v – заданное значение выходной координаты.
Управляющее воздействие имеет вид:	(1)
u= kx + Dv, (u,v) Rm , x Rn ,	(1)

D – квадратная матрица dimD = m× m.

Полагаем, что элементы матрицы k уже определены предыдущим алгоритмом синтеза модальным методом. Определим матрицу D из условия статики:

x&= Ax + Bu,y = Cx,

u = kx + Dv.

В статике x&= 0, x Rn . Т.к. det A ≠ 0:

0 = Ax0 + Bu x0 = −A−1Bu x0 = −A−1B(kx0 + Dv)

x0 = (I + A−1Bk)−1(−A−1BDv) y0 = Cx0 = C(I + A−1Bk)−1(−A−1BDv).

Т.к. рассматривается условие (1’), то можно записать

I = −C(I + A−1Bk)−1 A−1BD.

Из выражения (4) определяется требуемая матрица D. Структурная схема реализуемой системы (рис.112)

(2)

(3)

(4)

v	D	u x&= Ax + Bu x	C	y
		k
		Рис.112

В данной структуре обеспечены заданные статические и динамические свойства системы.

Учет возмущений

На реальную САУ в процессе работы влияют внешние возмущения. Их действие должно быть сведено до минимума выбором параметров регулятора. В противном случае поведение замкнутой системы будет сильно отличаться от желаемого.

Рассмотрим, как нужно уменьшить влияние возмущений:

&	+ Bu	+ F(t),
x = Ax	+ Bu	+ F(t),
		(1)
y = Cx,

u = kx + Dv,

(v,u, y) Rm , x Rn , F Rl

&
Рассмотрим статический режим, когда x = 0
0 = Ax0 + Bu + F(t) x0 = −A−1(Bu + F) x0 = −A−1(Bkx0 + BDv + F)	(2)
x0 = (I + A−1Bk)−1(−A−1BDv)+ (I + A−1Bk)−1(−A−1)F y0 = Cx0 =

= −C(I + A−1Bk)A−1BDv−C(I + A−1Bk)−1 A−1F.

Из выражения (2) видно, что матрица D во второе слагаемое не входит, в нем присутствует только матрица коэффициентов регулятора k . Следовательно, уменьшить влияние возмущений на выходные

координаты можно только с помощью коэффициентов матрицы	k , а они рассчитаны из условий
требуемых динамических свойств.
Статическая ошибка из (2)	(3)
ε = y0 − v = −C(I + A−1Bk)−1 A−1F .	(3)
При построении системы всегда требуется, чтобы ε ≤ εзад. , т.е. должно выполняться
− C(I − A−1Bk)−1 A−1F ≤ εзад. .	(4)

При рассчитанных значениях матрицы коэффициентов k проверяется, выполняется ли условие (4), если оно не выполняется, то необходимо изменять k , следовательно меняется и требуемое распределение корней.

Вэтом случае необходимо находить компромиссное решение при расчете элементов матрицы k .

Вобщем случае для многосвязных систем матрица k имеет размерность dimk = m× n, поэтому n элементов матрицы k рассчитываются из условия обеспечения заданных динамических свойств, а оставшиеся m элементов позволят обеспечить определенную ошибку в статическом режиме.

Определение коэффициента усиления разомкнутой САУ скалярной системы

При заданном объекте управления, вначале определяется нужна ли замкнутая САУ, чтобы обеспечить требуемую точность (ошибку) ε% в статике для всего заданного диапазона изменения

выходной координаты D = xmax .

xmin

ε0 % – ошибка объекта управления по возмущению.

xуст.


		ε0 % =		ε0		100%
		ε0 % =		xуст.		100%
				xуст.
	1.	Если ε% > ε0 %, то объект в разомкнутом состоянии
ε0	обеспечивает заданную ошибку ε%.
ε0	2.	Если ε% < ε0 %, то необходимо иметь замкнутую
	2.	Если ε% < ε0 %, то необходимо иметь замкнутую
	систему, причем
		ε% =	ε0 %		,	откуда
		ε% =			,	откуда
	f	1+ kp

Рис.113

kp =	ε0 %	−1.	(1)
	ε%

Т.к. при уменьшении величины x, относительная ошибка возрастает, то требуемый коэффициент усиления разомкнутой системы обычно определяется для xmin , тогда

ε% =	ε0 % D	,	kp =	ε0 % D	−1.	(2)


	1+ kp			ε%
Если kp удовлетворяет выражению (2)			(а практически берут с запасом),			то на всем диапазоне
изменения x будет поддерживаться выходная координата с точностью ε%.						k0 необходимо, чтобы
Следовательно: при известном коэффициенте усиления (передачи) объекта –
kp = k0ky . Отсюда определяется коэффициент усиления УУ.

ky = kk0p .

Для астатических (следящих) систем определяется требуемый коэффициент усиления по заданной скоростной ошибке

Ω

εск = kp ,

Ω – скорость изменения входного сигнала Ω = 1 рад/сек, тогда

kp =	1		.
	ε	ск

Далее определяются динамические свойства системы (если система неустойчива или при устойчивой системе получается неудовлетворительное качество) необходимо синтезировать корректирующее устройство.

Частотный метод синтеза

Этот метод активно развивался, начиная с 50-х годов. Он применяется, в основном, как графический и не позволяет получить точных оценок показателей качества, но является достаточно простым методом синтеза. Метод применяется, в основном, для синтеза линейных скалярных систем и иногда эффективно применяется для расчета нелинейных систем.

Для данного метода необходимо:

1.Задать математическую модель объекта в виде передаточных функций и от них перейти к частотным характеристикам.

2.Задать по заданным показателям качества желаемые частотные характеристики.

3.Задать структуру регулятора в виде корректирующего звена с помощью передаточных функций или частотных характеристик.

Существует два метода:

1.Последовательная коррекция.

2.Параллельная коррекция.

1. Последовательная коррекция.

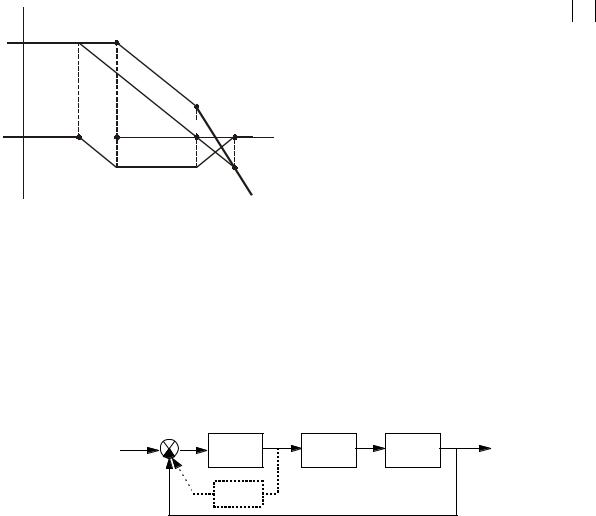
Имеем исходную систему (рис.114)

G(p)	W1(p)	X(p)
	W1(p)	W2(p)

Рис.114

Если исходная система неустойчива или не удовлетворяет заданным показателям качества ПП, то её необходимо скорректировать. Применяем последовательную коррекцию с пока неизвестной ПФ WK (p)

(рис.115)

G(p)	?		X(p)

	WK(p)	W1(p)	W2(p)

Рис.115

Требуется определить ПФ WK (p) , а затем и физические элементы, ей соответствующие.

Для этого: По известным показателям качества регулирования определяется желаемая передаточная (частотная) характеристика разомкнутой системы W* (p), тогда

W (p) = W (p) W (p) W (p) = W* (p)
p	K	1		2
откуда
WK (p) =		W* (p)		.	(1)
WK (p) =	W1	(p) W2	(p)	.
	W1	(p) W2	(p)

От (1) перейдем к частотным характеристикам в логарифмическом масштабе. Для этого прологарифмируем (1) при p→ jω

20lg

= 20lg

− 20lg

W1W2

(2)

График вычисления последовательного корректирующего устройства по частотным характеристикам в обычном масштабе (рис.116)

(ω

) =

(ωi )

)

(ω

-1,j0

ω3

ω=∞

ϕK (ωi )

= ϕ

(ωi )−ϕ1

(ωi )−ϕ2 (ωi ).

ω2

ω=0

ω1

ω2

W1W2

ω1

Рис.116

График вычисления последовательного корректирующего устройства по частотным характеристикам в логарифмическом масштабе по выражению (2) (рис.117)

20lgA(ω)

20lg\|W1W2\|
	-
	2
		0
		д
		б
*		/
20lg\|W \|	-	к.
	2
	0
		д
		б
		/
		д
		е
		к
		.
ω1	ω2	20lg\|WK\|
-2		20lg\|WK\|
0		0
		0

Рис.117

ω 3

20 +

ω4 lgω

- 4

б / д

к .

По полученному виду ЛАХ 20lgWK по

таблицам стандартных фильтров (RC-цепочек) (табл. 2 на стр.83), определяется соответствующая схема корректирующего устройства, параметры сопротивлений и емкостей зависят от численных значений ω1 ,ω2 ,ω3 ,ω4 .

W (p) =	(T2 p + 1)(T3 p + 1)	,

K	(T1 p + 1)(T4 p + 1)

где	T =	1		, T	=		1		, T	=		1		, T	=		1		.
		ω				ω					ω
	1		1	2				2	3				3	4		ω		4

Недостатки последовательной коррекции:

1.В некоторых САУ невозможно разорвать главный контур регулирования, следовательно, невозможно включить последовательную коррекцию.

2.Низкая помехозащищенность, т.к. корректирующие звенья в основном дифференцирующие, то в них возрастают высокочастотные помехи.

Эти недостатки отсутствуют у параллельной коррекции.

2. Параллельная коррекция.

Рекомендации по месту включения корректирующего звена:

2.1.Необходимо охватывать звенья с наибольшим коэффициентом усиления.

2.2.Не рекомендуется охватывать много инерционных звеньев, т.к. сам контур может оказаться неустойчивым (если все же по условиям приходится охватывать инерционные звенья, тогда внутренний контур по любому критерию необходимо проверить на устойчивость).

G(p) E(p)	W1(p)	x(p)
W1(p)	W1(p)	W2(p)
WK(p)

Рис.118

Как и при последовательной коррекции по заданным показателям качества определяется W* (p)

разомкнутой системы, тогда	W1(p)
	W1(p)		*			(1)
Wp (p) =				W2 (p) W3(p) =W	(p),
Wp (p) =	1+W	(p)W	(p)	W2 (p) W3(p) =W	(p),
	1	K

обозначив W1W2W3 =WH – ПФ нескорректированной разомкнутой системы и решая относительно WK , получим

	W (p) −W* (p)		(2)
W (p) =	H	.
W (p) =	W (p)W* (p)	.
K	W (p)W* (p)
	1

Уравнение (2) является исходным для определения ПФ параллельного корректирующего звена. Если коэффициент усиления разомкнутой системы достаточно большой (большинство реальных

систем), то синтез параллельного корректирующего звена ведут по ”вырожденным структурам”.

Параллельная коррекция по вырожденной структуре


Заменяя в (1) p = jω , получим частотные характеристики
W	*	( jω) =	W1( jω) W2 ( jω) W3 ( jω)		.	(3)
W		( jω) =	1+W ( jω)W ( jω)		.
			1	K

В области частот работы системы (область средних и высоких частот) W1( jω) WK ( jω) >>1, поэтому

Электрические схемы, передаточные функции, ЛЧХ типовых корректирующих устройств Таблица 2

1 / 21 2 > Следующая >>>

Соседние файлы в папке Кошкин Ю.Н. ОТУ

#
23.01.2019543.42 Кб21tau_1.pdf
#
23.01.2019909.77 Кб15tau_2.pdf
#
23.01.20191.72 Mб15tau_3.pdf
#
23.01.2019807.35 Кб15tau_4.pdf
#
23.01.2019777.29 Кб16tau_5.pdf
#
23.01.2019771.74 Кб15tau_6.pdf
#
23.01.2019788.43 Кб16tau_7.pdf