Bilety_po_matanu_tolko_praktika

Билет №1

3)

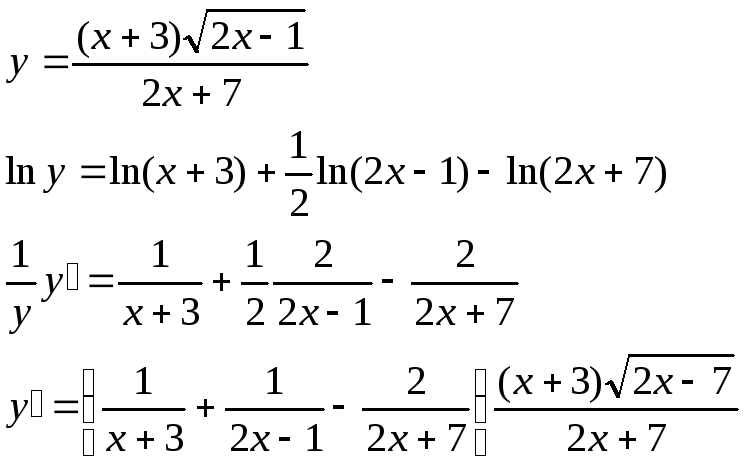
4)

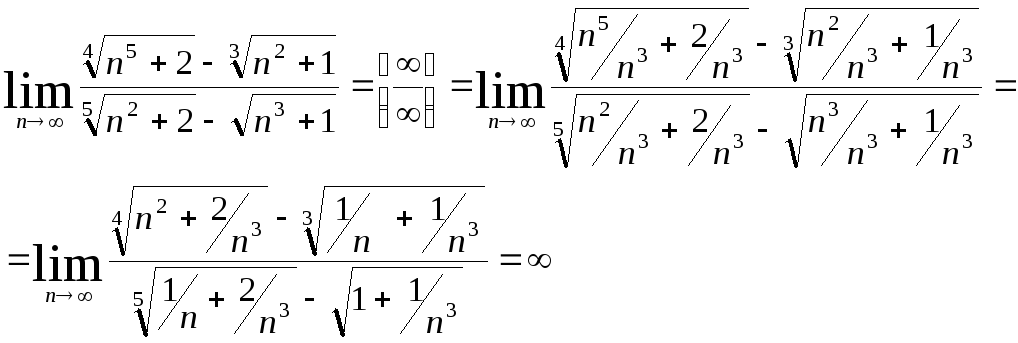
5)

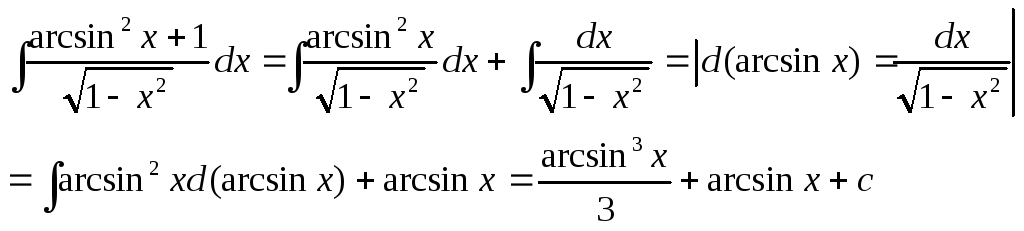
Билет № 2

3)

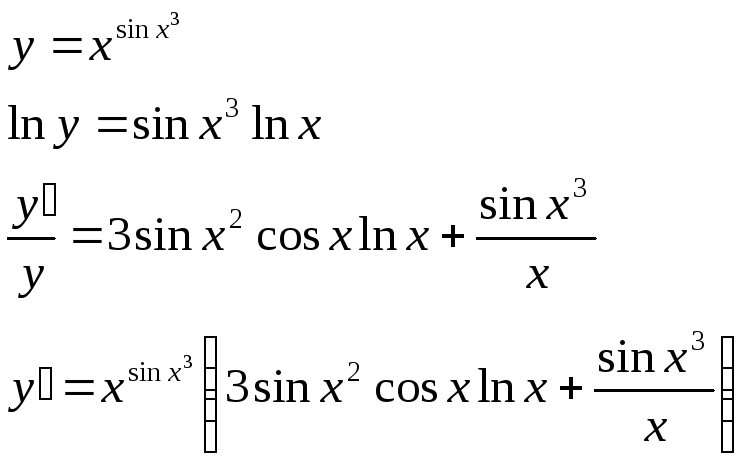
4)

x		(-1)	(-1;0)	0
	---	0	---		+
y	♀		♀	max	♂

5)

Билет № 3

3)

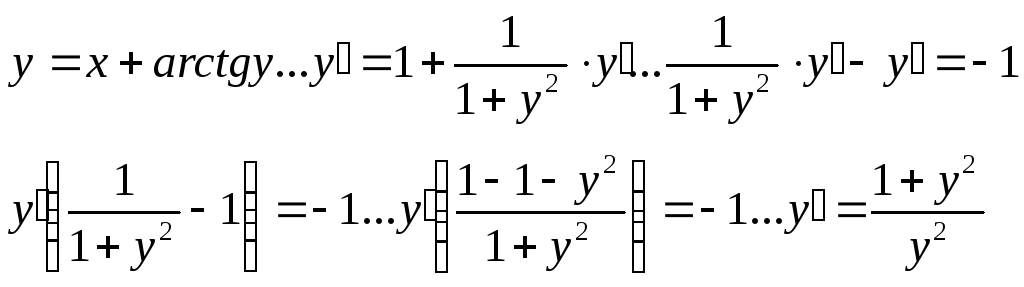
4)

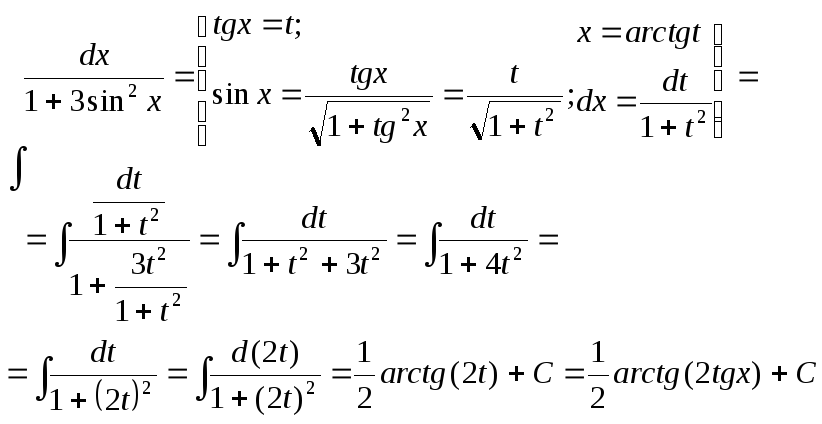
5)

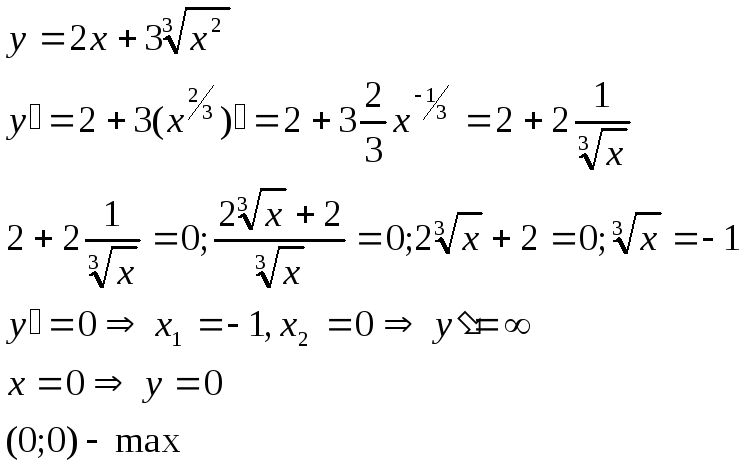
Билет № 4

3)

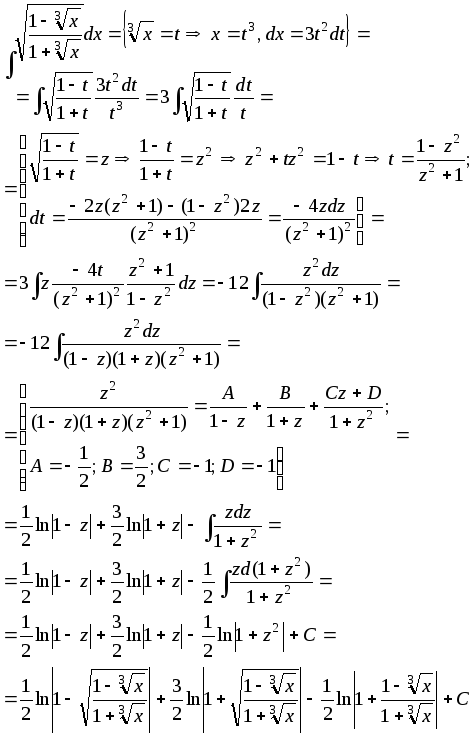
4)

5)

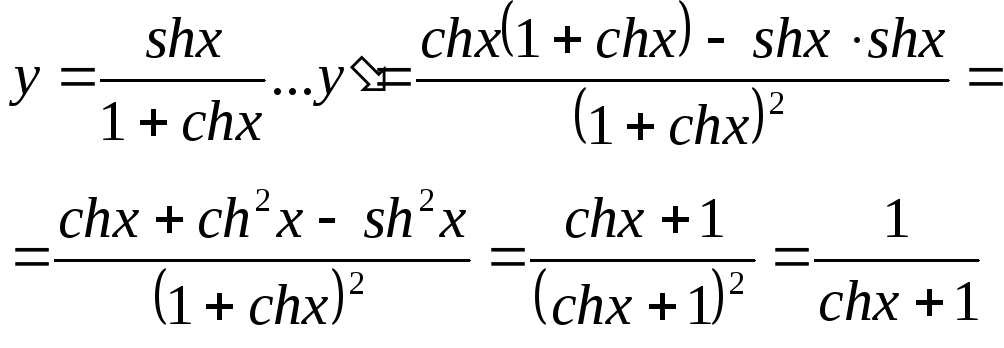
Билет № 6

3)

4)

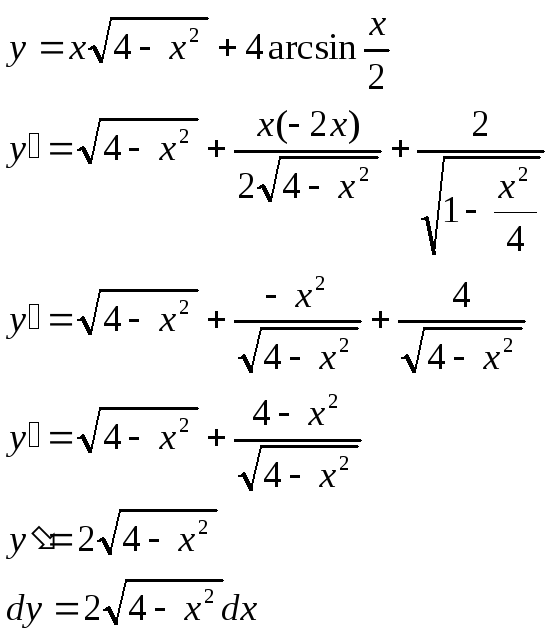
5)

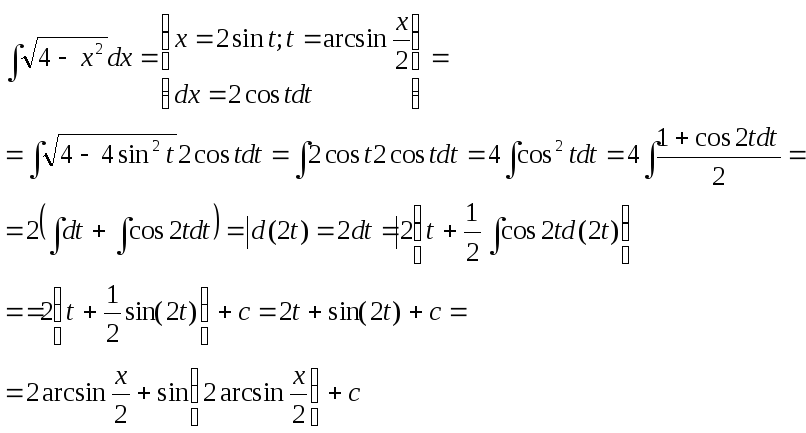
Билет № 8

3)

4)

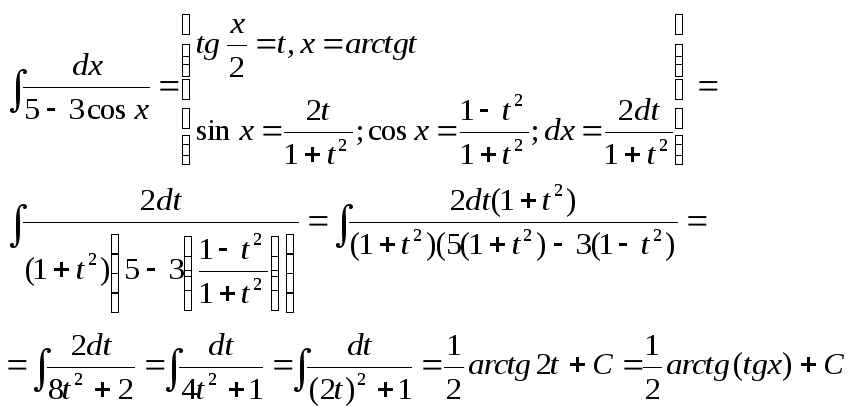
5)

Билет № 7

3)

4)

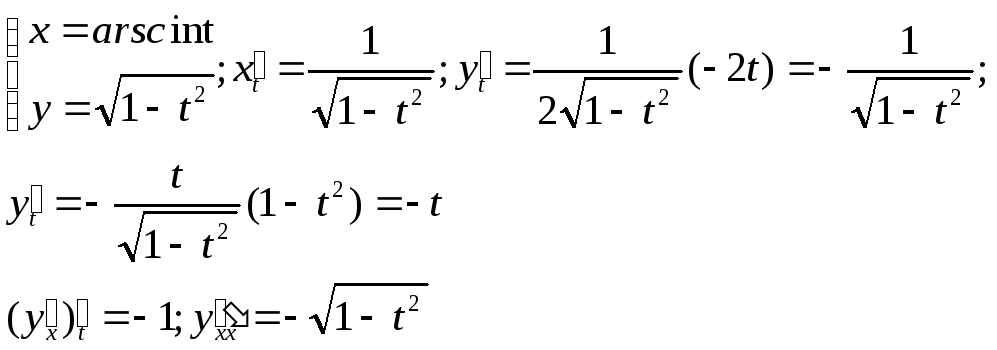
5)

Билет № 9

3)

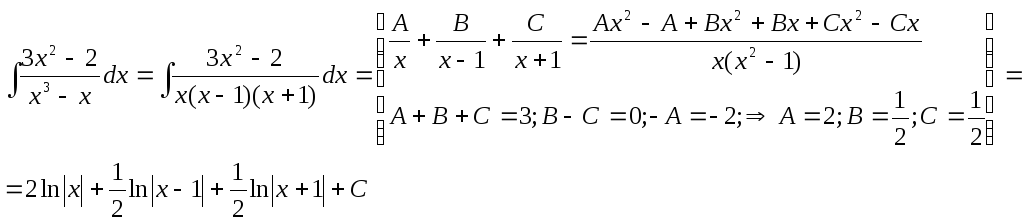
4)

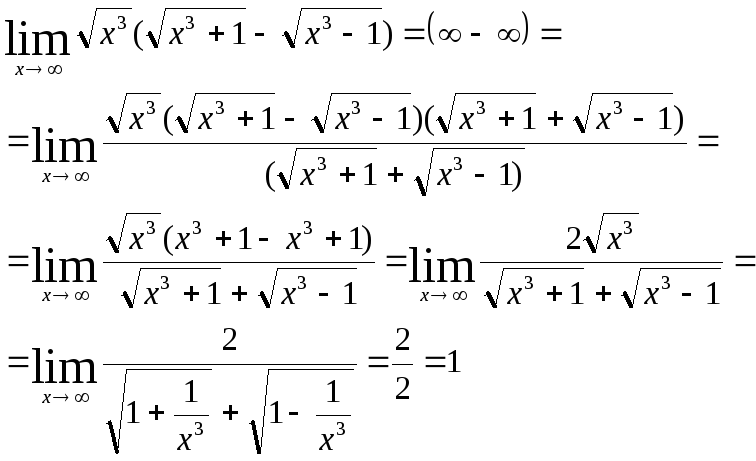
5)

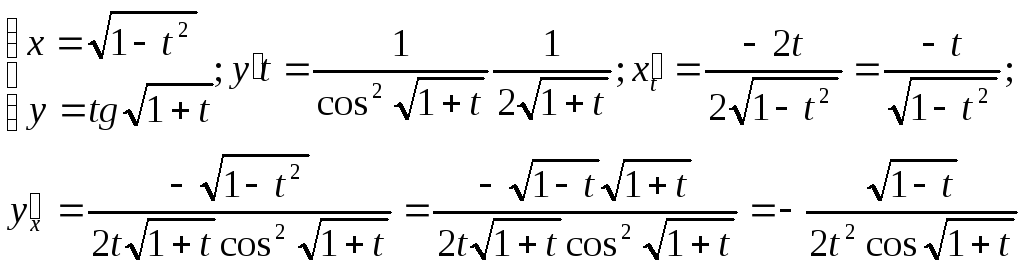
Билет № 11

3)

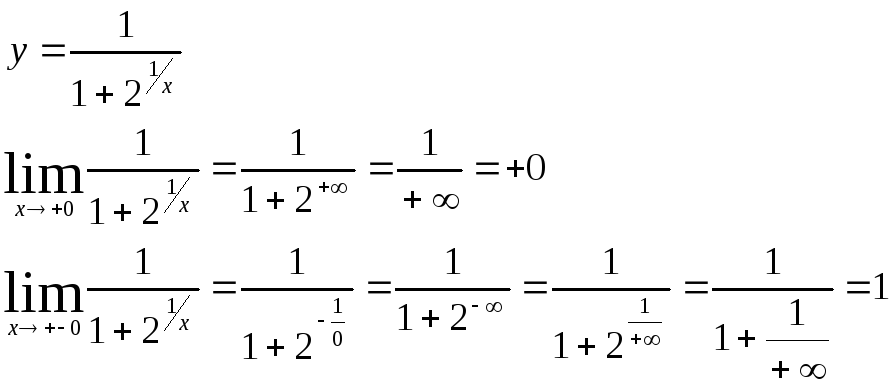
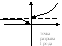
4)

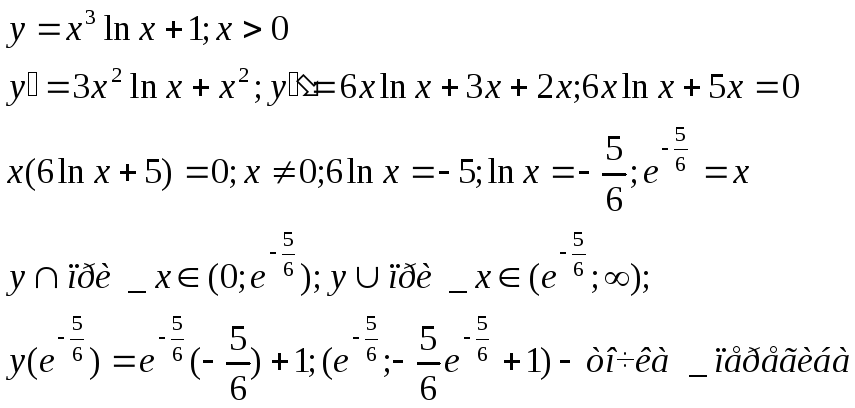
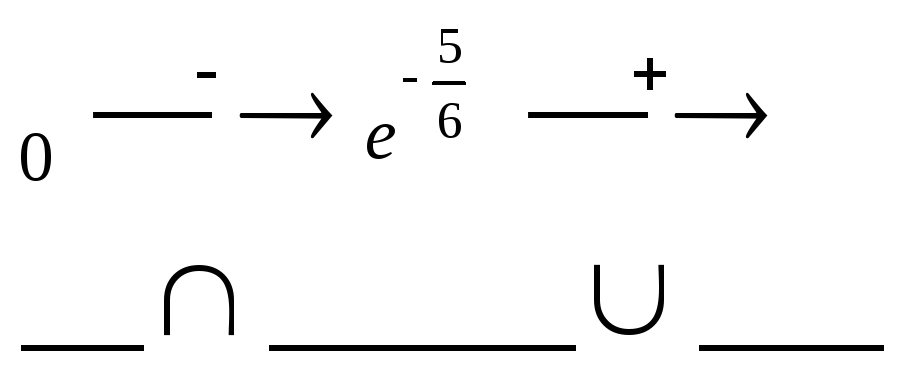
5)

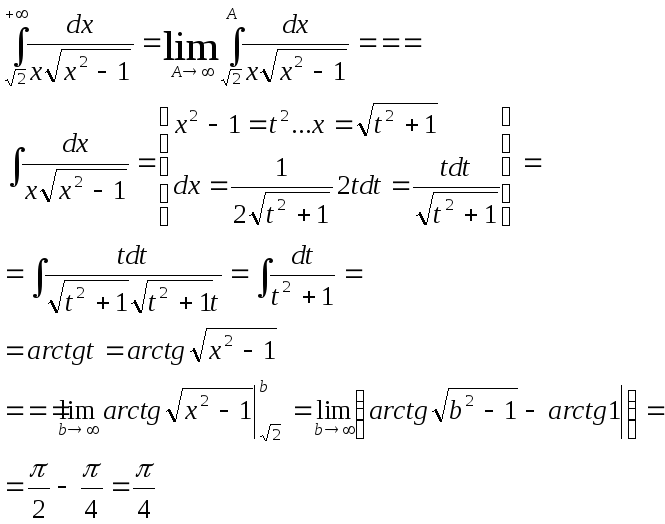
Билет № 13

3)

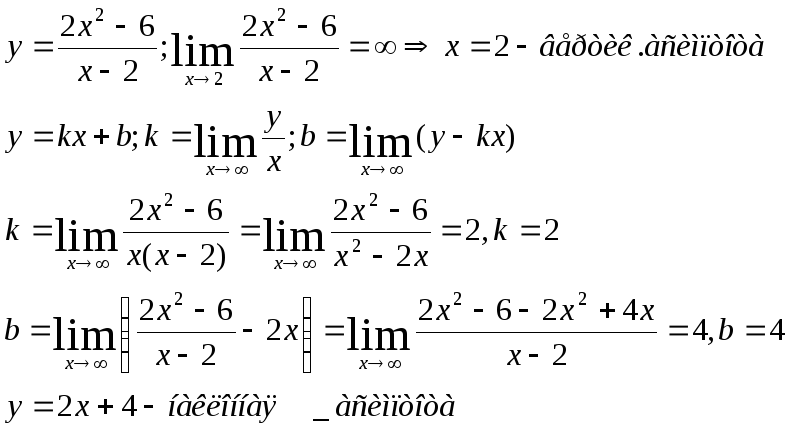
4)

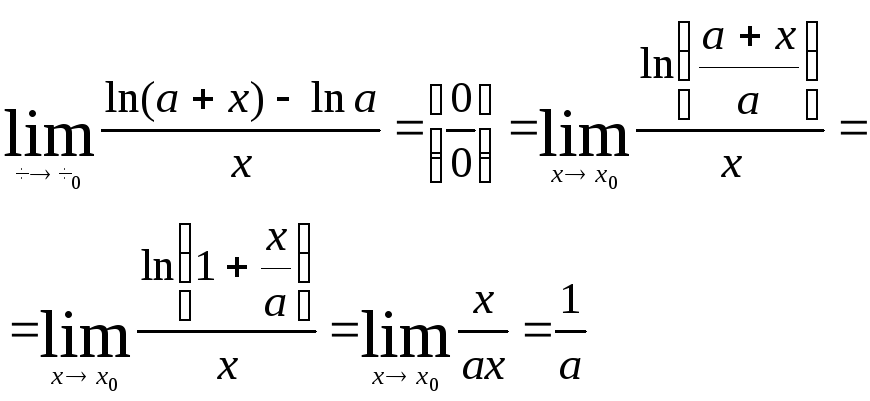
5)

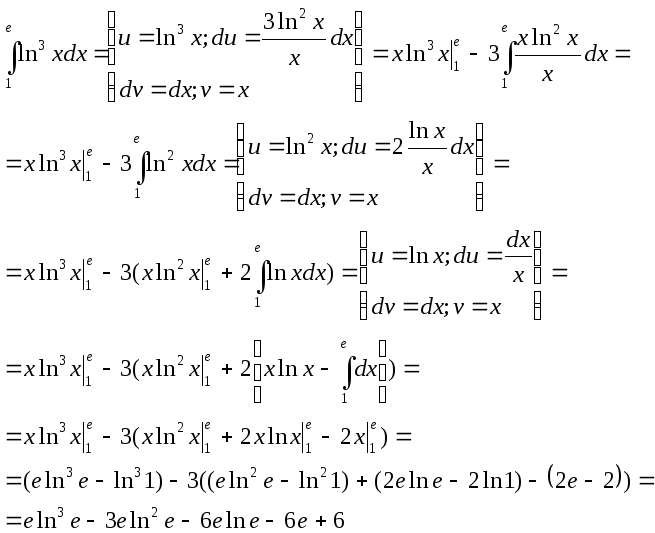
Билет № 14

3)

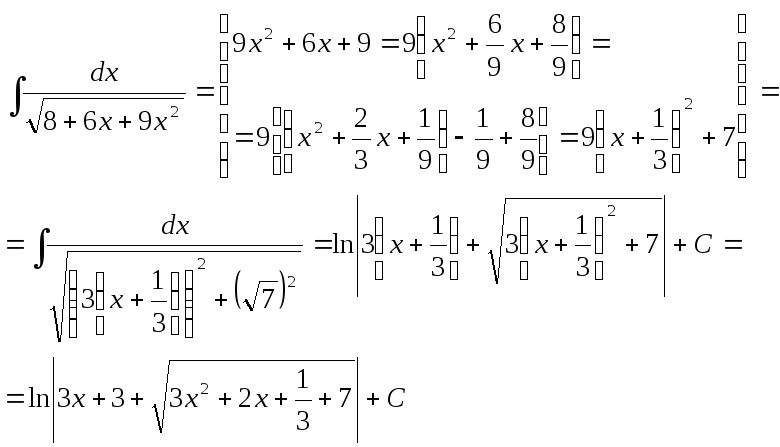
или

4)

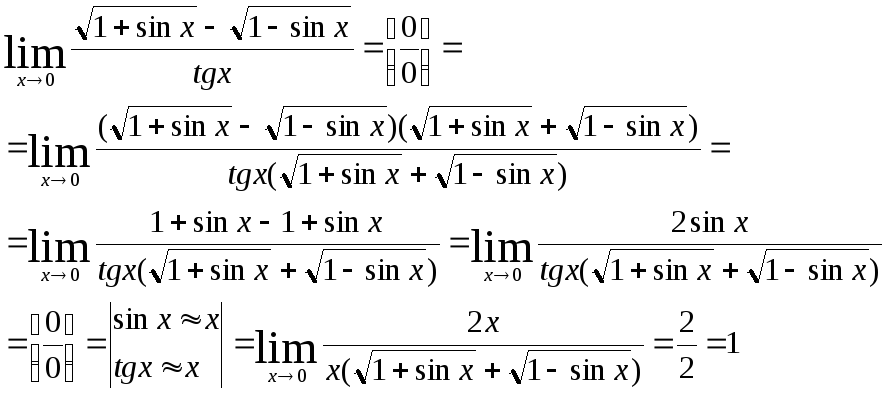
5)

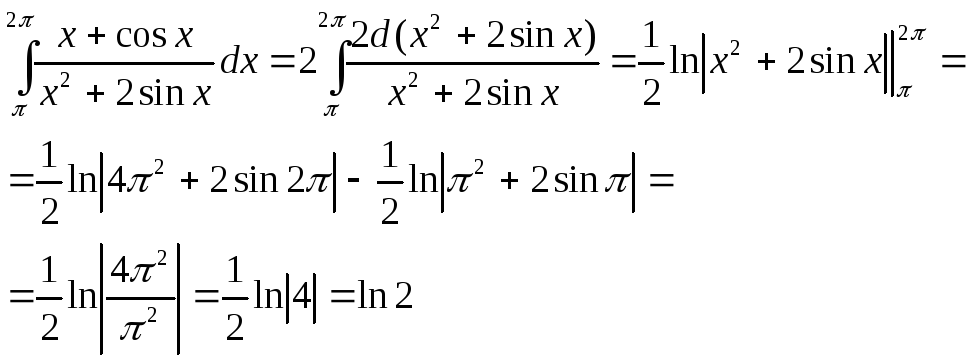
Билет № 15

3)

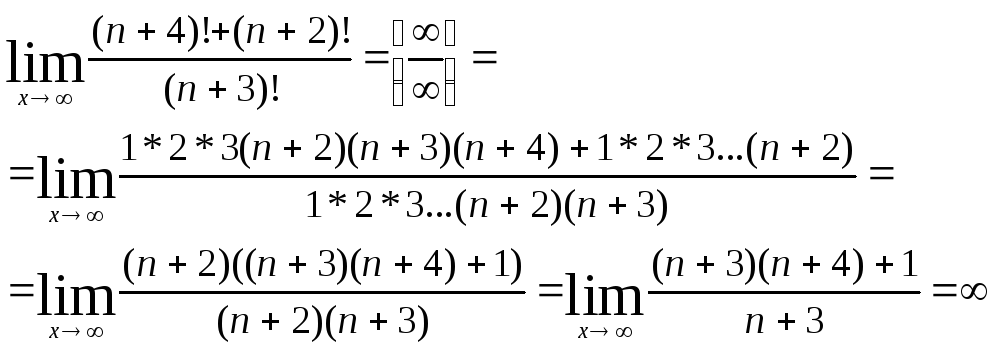
4)

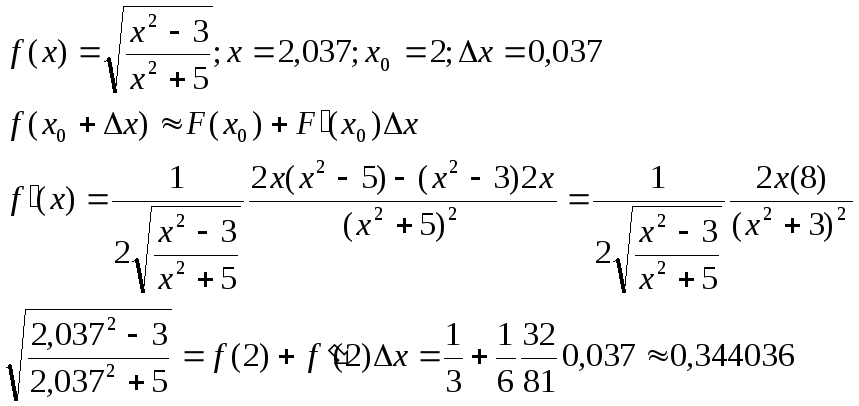
или

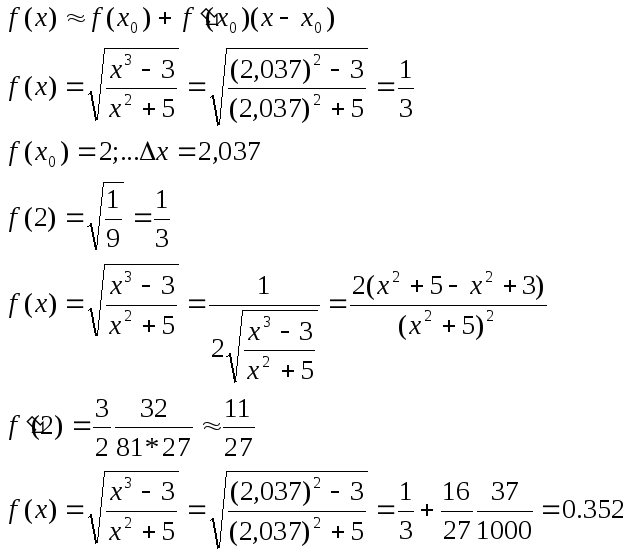
5)

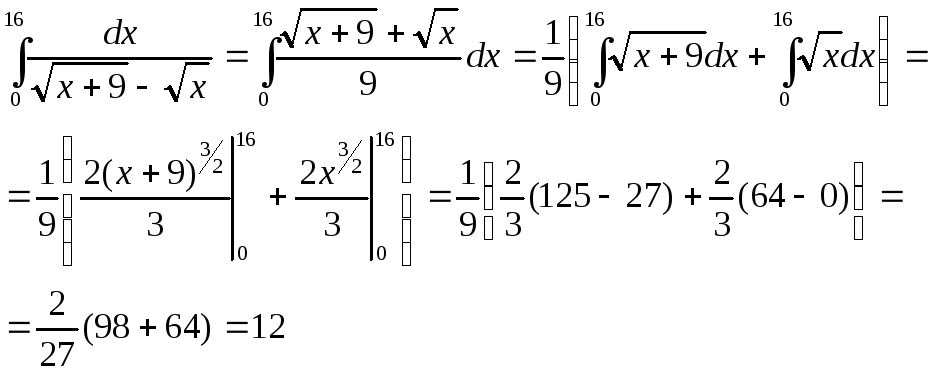
Билет № 16

3)

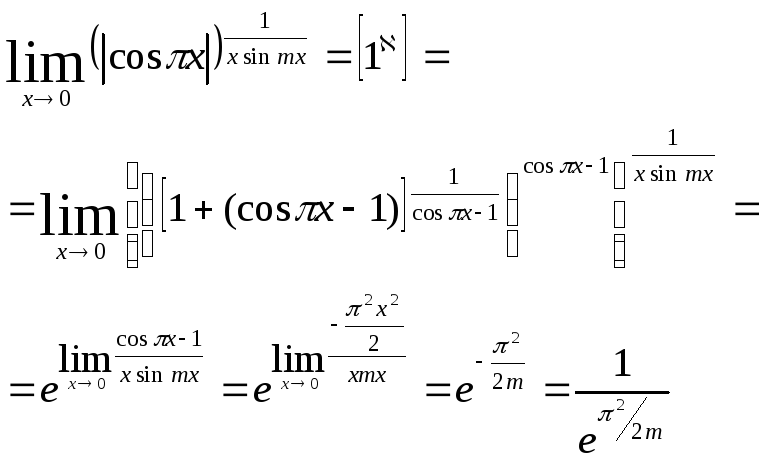
4)

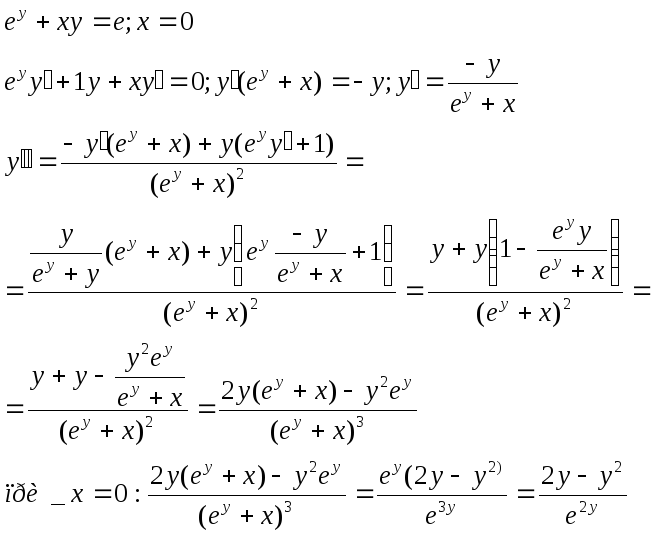
5)

Билет № 18

3)

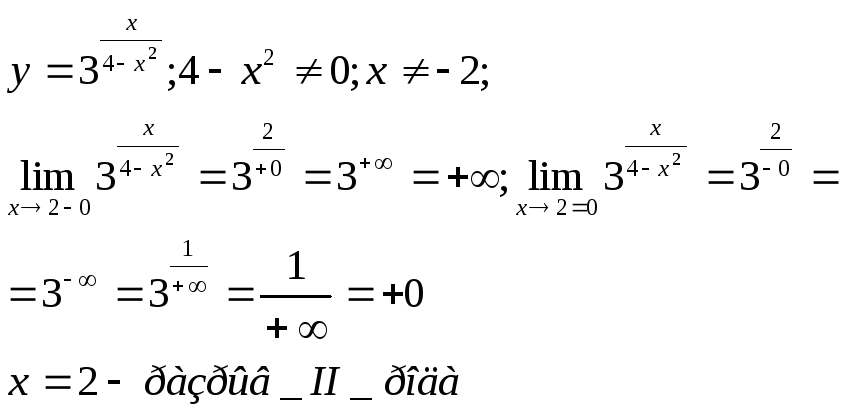
4)

5)

Билет № 19

3)

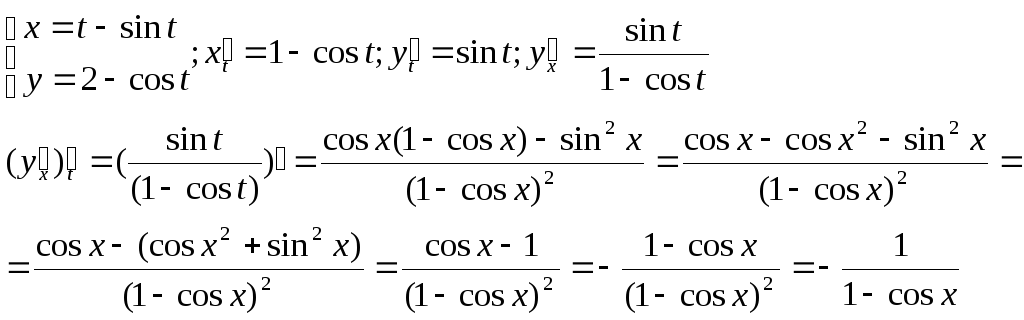
4)

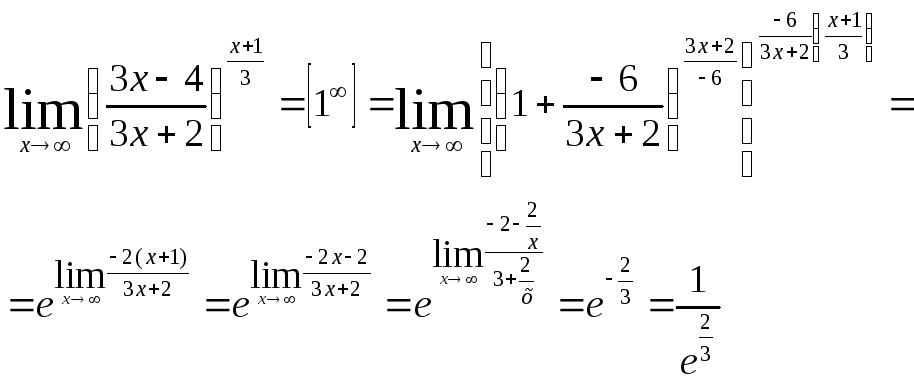
5)

Билет № 21

3)

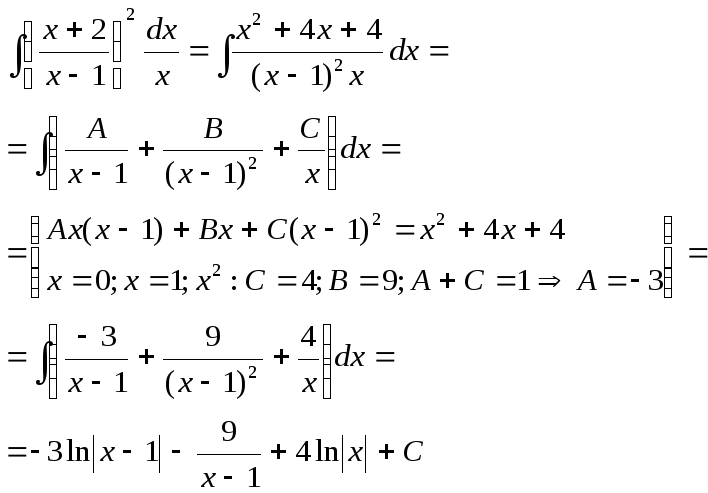
4)

5)

Билет № 22

3)

4)

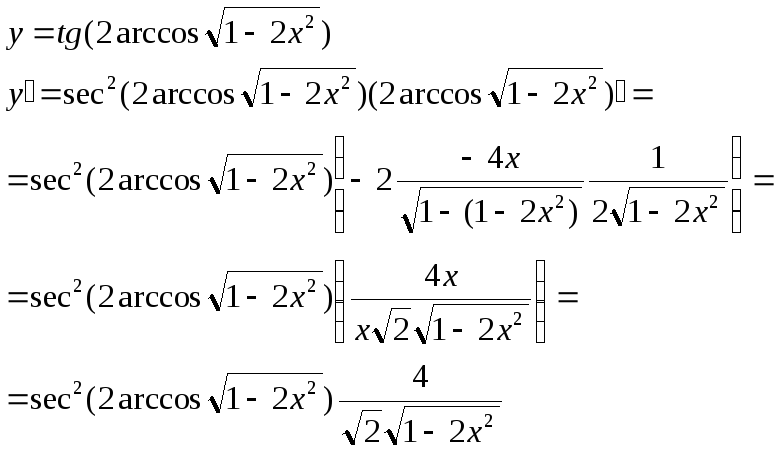
5)

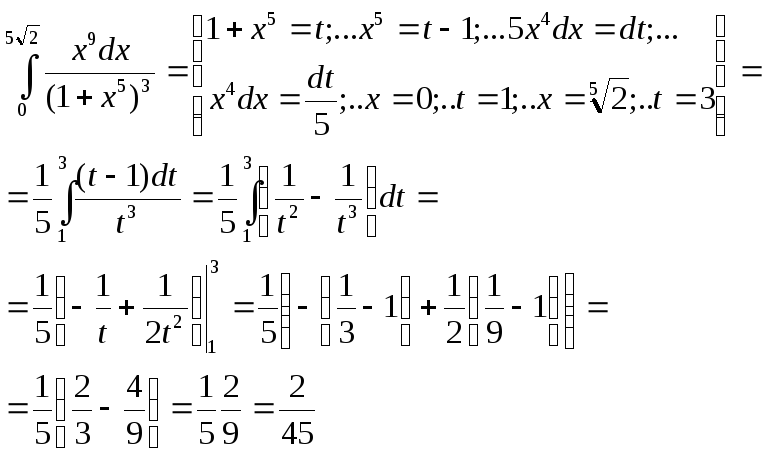
Билет № 24

3)

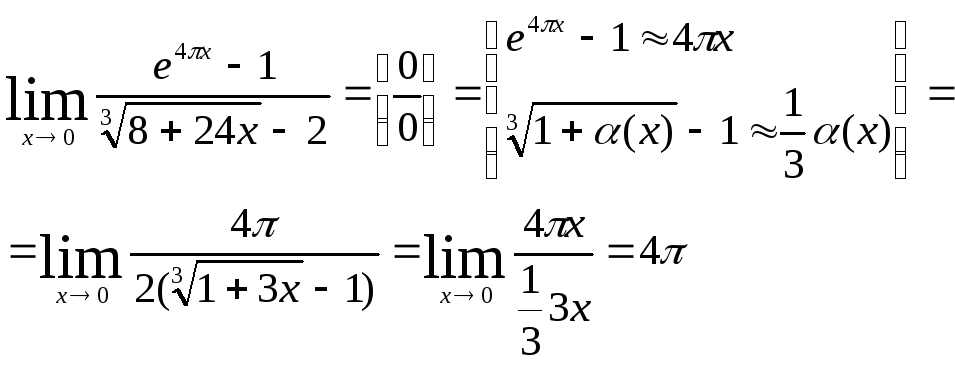
4)

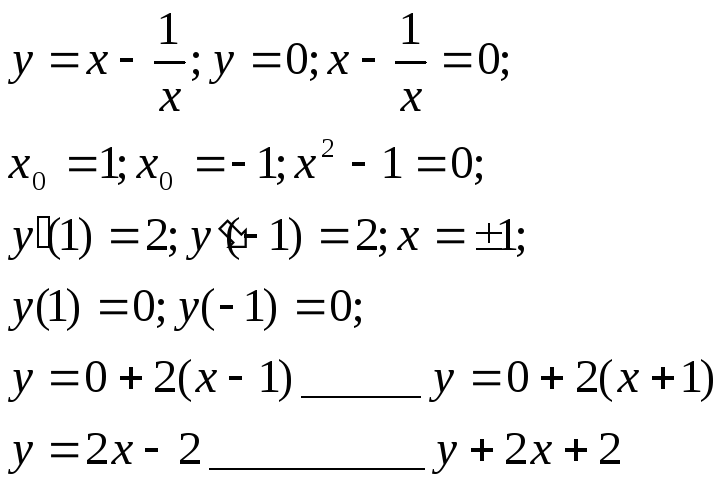
5)

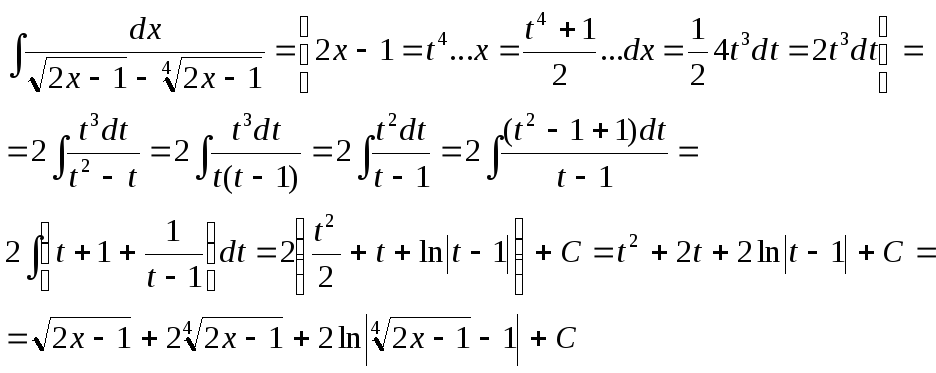
Билет № 25

3)

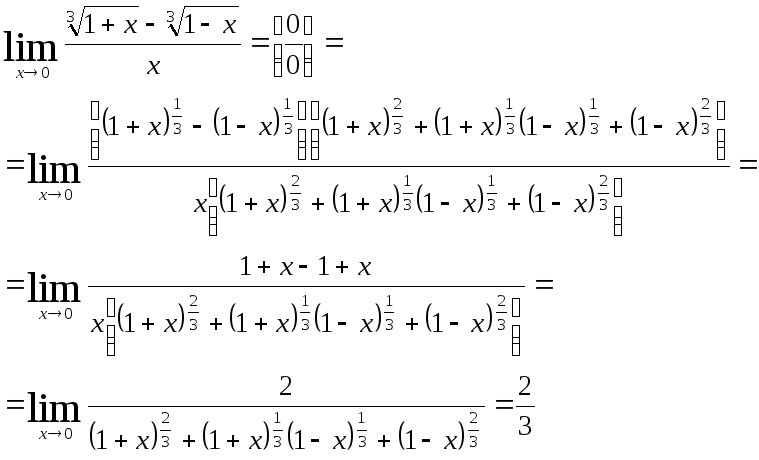
4)

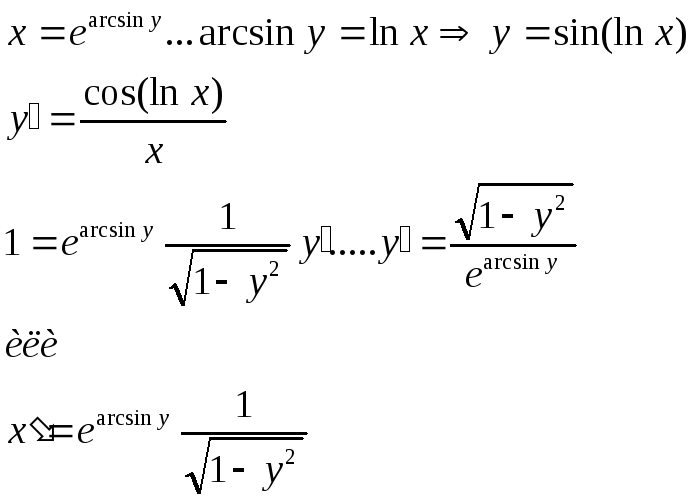
5)

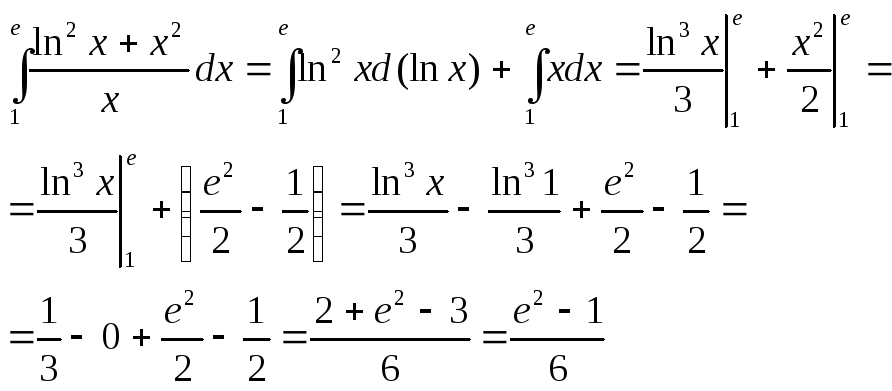
или

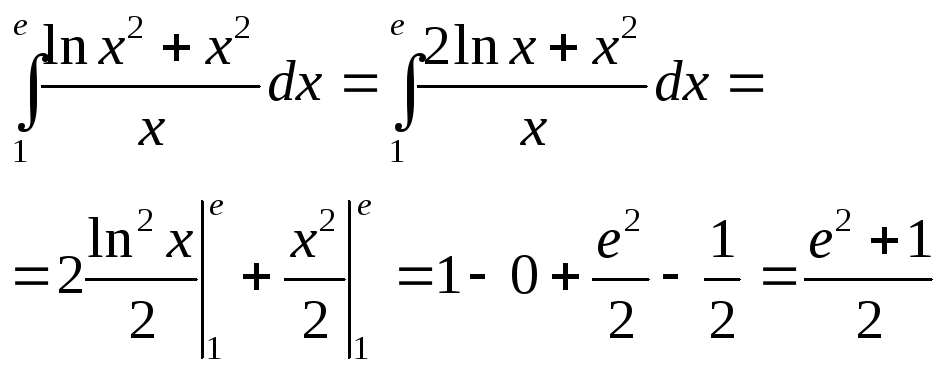
Билет № 12

3)

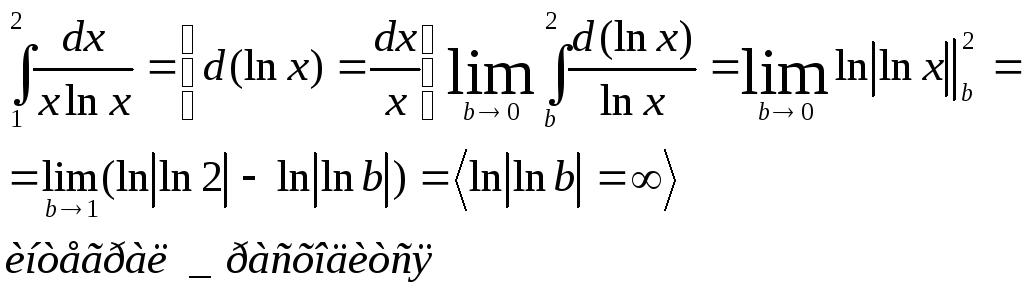
4)

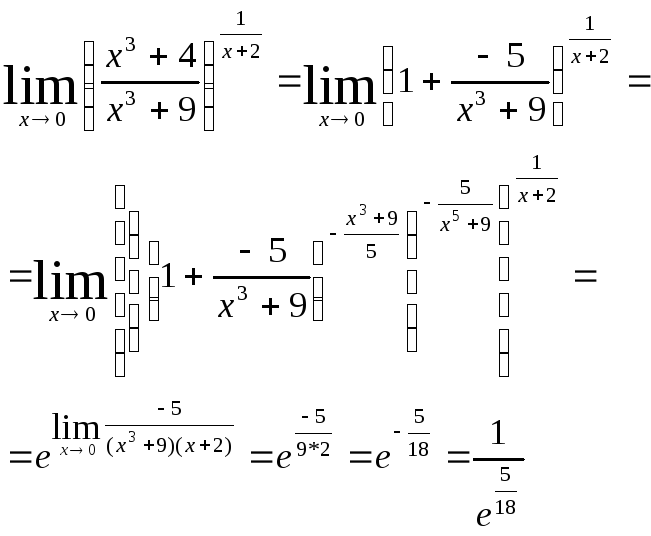
Билет № 5

1) ВОПРОС Предел монотонной ф-ции 1 и 2 замеч. пределы.ОТВЕТ Пусть дана монот. возр. посл. Если она огранич. сверху:то необход. имеет конечн.предел, иначе она.ДОКАЗ Допустим что переменная огранич. сверху, тогда для множее знач. должна сущ. и конеч. верхн. границаименно это число и будет пред. посл. Действ.,во-первых для всех знач.будетво-вторых какое бы ни взять найд. такое значкоторое превзойд.,.Так как ввиду монот. перем, при будетт.е. и подавно, то для этих знач номеравыполн. нерав-ватак чточ.т.д.Пусть послед.не огран.сверху,тогда сколь ни велико было бы найдется хоть одно знач. посл. большее ,ввиду монот.дляи подавно 1 ЗАМЕЧ|| докажемпри(1)для этого в круге радиусарассмотрхордуи касат.к окр.в т.. Имеем сект..Радианн.меру обозн.за т.что длина дуги = сокр.на и разделим на кажд.из членов. нер-ва ; но в силу (1)это нер-во и реш. вопрос.2 ЗАМЕЧДОКАЗ:. кажд.знач.закл. между 2 плож. цел.числамивыполн. нерав. еслито инайдем

=;

Пустьвведем или

чтд

2)ВОПРОС Опр.интегр.и способы его вычисл.Определ.Пусть задана на.Разобьем произв. этот промеж. Наиб.из разност.будем обозн.возьмем в кажд. из промеж.произв. точку ; и состав. суммуУстанов. понятие кон. предела Представим себе бескон. число рабиен.тогдасход.к нулю. понимаем:что посл. знач. суммы отвеч. любой основ. послед. разбиений промеж.всегда сход. к пределу как ни выбир. при . Кон. предел суммыприесть опр. интегр ф-циив промеж от доесли предел сущ то назыв интегрируем в промеж Числаиесть нижн и верх пределы ентеграла.Методы выч: осн ф-ла (А) Замена переменной Пусть надо выч. гденепр наПоложимподчинив ее услов.1) опр и непр на ее знач не выход пред промеж, когдаизмен 2), 3)сущ в непр произ тогда имеет местоимеем одновр По частям в предпол. что ф-ции ,от независ. перем. непр. в рассм. промеж.вместе с произв.Обозн. посл инт. через тогда по ф-ле(А)в то же время в силу (А) имеем оконч.

3)

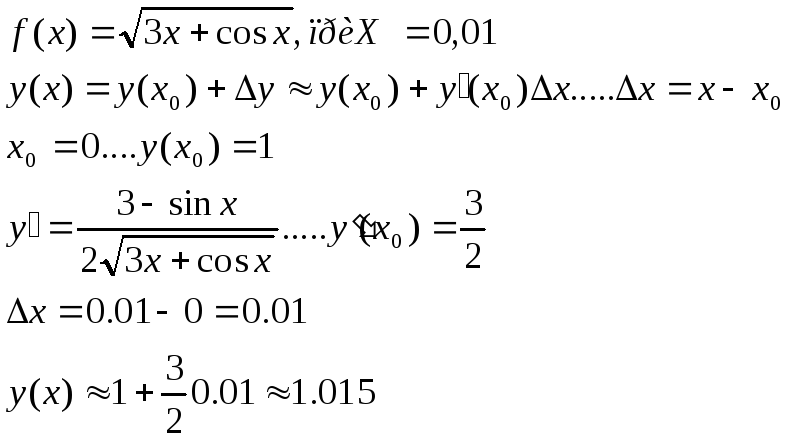
5)

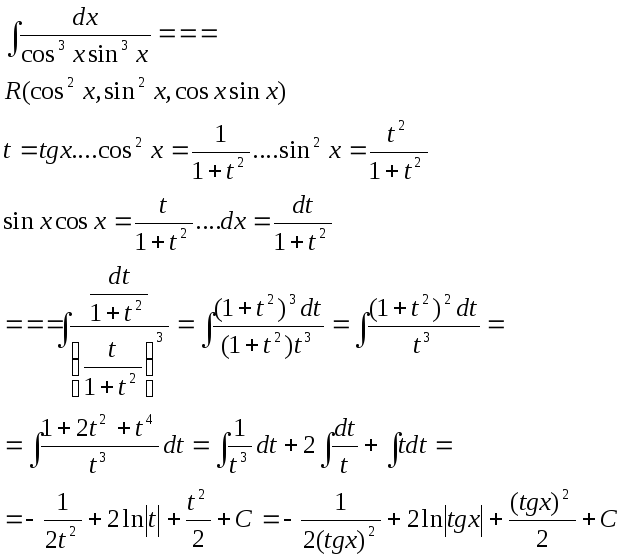
Билет № 20

1) ВОПРОС: Теорема Лагранжа, Коши. ОТВЕТ: {Т.Л.}Пусть опред. , сущ. конеч. произв. во всех внутр. точках , тогда между точками a и b найдтся точка сб в кот. выполн. равенство . . {Док-во} Введем вспом.ф-ии 1)Дан.ф-ия 2)... Удовл. теор.Ролля дан.ф-ия ч.т.д. {Т.К.} Пусть ф-ии и непрерывны на , дифференцируемы на и . Тогда сущ., по крайней мере, одна точка такая, что . {Док-во} . Введем , . удовлет.т.Ролля . Формула явл.частным слчаем ф-лы . Замеч.: нельзя в док-ве т.Коши использовать ф.Лагранжа для числителя и знаменателя. . ч.т.д.

3)

4)

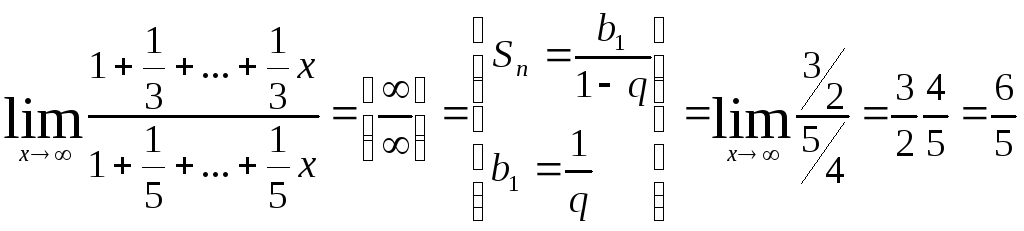
Билет № 23

2) ВОПРОС св-ва опр инт и теор о среднем ОТВЕТ1!Еслиингегр в то она интегр. и в промеж, причем по опр интегр. при в предполож. что интегр. сущ. также по опр полаг. 2!Пусть интегр в наиб из промеж то она интегр и в двух других и имеет место при любом располож. точек ДОКАЗ. Положим и ф-ция интегр. в Рассмотр. разбиен в на части, причем одна из т. деленввиду положит.всех слаг.из стремл. к 0 сумм слева следует то же и для правых сумм, так что инт-мость в промежиустановл. очевиднопереходя к пред. при получ требуемое рав-во.

3!Если интегр. в , то и также интегр. и 4!Если иинтегр в то тоже интегр причем ДОКАЗ. Разобъемна чясти и сост. интегр суммы причем т. на кажд. промеж выбир. произв-но но для всех сумм одни и те же Переходя к пред и приход. к требуем. соотн.5! Если интегр-ая нанеотр. то6!Если и и интегр. на и то и Применить (5) к7! Пустьинтегр в и тогдаинтегр. и имеет место ДОКАЗ. Убедимся в . Если в промеж. взять любыеито обозн через колеб-е в имеем стремл к 0 суммы справа влечет то же слева Самое нер-во получ из и пер-дя к пред

8

!Еслиинтегр вгде и если во всем промеж имеет место тоДОКАЗи перейти к пределу.9!Теор. о средн. значении.Пустьинтегр. наи пусть во всем промеж.

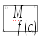
тогдагде ДОКАЗ. Если то по св (8) имеем положив получ требуем. рав-во.Если, проводим то же рассужд. для ф затем, переставив

пределы переходим к прежней ф-ле.ГеометрПусть . Рассмотр. кривол-ную ф-ру под кривойтогда площ. выражен. кривол. интегр. = площ. прямоуг. с тем же основ и с некотор. ордин в качестве высоты.10!Пусть1) и интегр в2)3)не меняет знака о.требуем. промеж. меет место е слева