dolgih

142	Г л а в а 13. Ряды Фурье. Интеграл Фурье

Пример. Представить рядом Фурье в комплексной форме периодическую функцию f (x) (T 2 ) , определенную для 0 x 2

равенством f (x) ex .

Построим график данной функции (рис. 13.3).

у

e2

		1
–4	–2	O	2	4	x

Рис. 13.3

Функция является кусочно-гладкой на [0; 2 ] , следовательно, ее можно разложить в ряд Фурье, который будет иметь вид

1 c einx .

2 n

c 1

n

1 2 ex(1 in)dx

0

			1		2
	f (x)e inxdx
					0
	1	ex(1 in)			2
	(1 in)				0

				1	2
	f (x)e inxdx				exe inxdx
					0
		1	e2 i2 n 1			e2 1
							.
		(1 in)				(1 in)

	e2 1										ex		, 0 x 2 ;
						1				inx
Ряд Фурье:									e		e2 1
	2					1 in									, x 0; 2 .
													2
	Задачи для самостоятельного решения
1. Разложить в ряд Фурье на (0;													2 )		функцию	f (x)		x .
																			2
2. Разложить в ряд Фурье периодическую (T 2 ) функцию																					f (x) ,
																			x
						3									cos x,		2					2	,
определенную на					,			равенствами f							(x)	x			3
				2		2									0,					.
																2			2

13.4. Интеграл Фурье. Преобразования Фурье					143
3.	Разложить в ряд Фурье на ( ,	)	f (x) x cos x .
4.	Разложить в интервале (0; )	по синусам f (x)			. Полу-
				4

ченное разложение использовать для суммирования числовых рядов:

а)	1		1		1		1	... ; б)	1	1		1		1		1			... .
		3			5		7		5			7		11		13
		5. Дана						функция f (x) x2 .									Разложить ее в ряд Фурье:
а)	в	( ; ) ;						б) в (0;	2 ) ; в) в					(0;			)		по синусам; г) в интервале

(0; ) так, чтобы сумма ряда тождественно равнялась нулю для всех x ( ; 0) .

6. Разложить в ряд Фурье f (x) x на [–1; 1].

x,	0	x 1,
	1 x 2,
7. Разложить в ряд Фурье f (x) 1,
3 x,		2 x 3

на [0; 3].

8.Разложить в ряд Фурье по косинусам f (x) sin

9.Доказать справедливость равенства

x на [0; 2].

2

			2			4		( 1)n 1
	cos x								cos 2nx .
								4n2 1
							n 1
10. Представить рядом Фурье в комплексной форме периодиче-
скую функцию f (x) (T 2 ) , определенную для										0 x 2 равен-

ством f (x) ex . Воспользовавшись полученным рядом Фурье в

комплексной форме, записать в действительной форме ряд Фурье этой функции.

11. Разложить в ряд Фурье f (x) (c периодом 2 ) в комплекс-

0, x 0,

ной форме: f (x) xe , 0 x .

12.Разложить в ряд Фурье f (x) сh x на [ ; ] .

13.Разложить в ряд Фурье f (x) sh x на ; .

13.4.ИНТЕГРАЛ ФУРЬЕ. ПРЕОБРАЗОВАНИЯ ФУРЬЕ

Теорема 2. Если f (x) : 1) абсолютно интегрируемая на

( ;	) функция, т.е. удовлетворяющая условию			f (x)		dx ;

2) кусочно-гладкая на каждом конечном отрезке, то ее интеграл Фурье

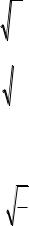
144	Г л а в а 13. Ряды Фурье. Интеграл Фурье

a( ) cos x b( ) sin x d ,

0

где

1

a( )

f (t) cos tdt ,

1

b( )

f (t) sin tdt ,

равен

f (x) в

каждой

точке непрерывности

f (x 0) f (x 0)

в каждой точке разрыва f (x) .

2

Если f (x) – четная, то

2

a( )

f (t) cos tdt , b( ) 0 .

0

(13.11)

(13.12)

(13.13)

f (x) и

(13.14)

Если f (x) – нечетная, то

			2
	a( ) 0 ;	b( )			f (t) sin tdt .	(13.15)
				0

Для представления интегралом Фурье функции, заданной лишь в промежутке [0; ) и продолженной четным образом на

( ; 0) , используем формулы (13.14), а продолженной нечетным образом – формулы (13.15).

Если a( ) и b( ) , найденные по формулам (13.14), подставить в (13.11), то получим двойной интеграл Фурье для четной функции f (x) :

		2
	f (x)		cos td f (t) cos tdt .
			0							0
	Положив
					2
	(x)									f (t) cos xtdt ,
	получим									0
				2
	f (x)									(t) cos xtdt .
										0
	Равенство (13.16) называется									косинус-преобразованием
	а (13.17) – косинус-преобразованием (x) .
	Аналогично, если f (x)			– нечетная, то

(13.16)

(13.17)

f (x) ,

2

(x) f (t) sin xtdt (13.18)

0

13.4. Интеграл Фурье. Преобразования Фурье	145

называется синус-преобразованием

f (x) , а

2

f (x)

(t) sin xtdt

(13.19)

0

называется синус-преобразованием (x) .

Комплексная форма интеграла Фурье имеет вид

1

c( )ei xd ,

(13.20)

2

где

c( )

f (t)e i t dt .

(13.21)

Связь между a( ), b( ) и c( ) :

c( ) (a( ) ib( )),

.

Функция c( ) называется спектральной характеристикой

функции f (x) ,

c( )

называется спектром функции

f (x) .

Функция c( ) называется также преобразованием Фурье

функции f (t) , в этом случае ее обычно обозначают

F ( ) f (t)e i t dt .

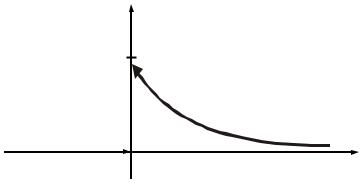
Пример. Представить интегралом Фурье функцию

x

,

x

1,

f (x)

x

1,

0,

1

,

x

1.

2

Построим график данной функции (рис. 13.4).

y

1

1/2

–1

0

1

x

Рис. 13.4

146

Г л а в а 13.

Ряды Фурье. Интеграл Фурье

Данная

функция:

1) имеет

2

точки разрыва

I

рода

(x 1) ;

2)

абсолютно

интегрируема

на

всей

оси

Ox:

f (x)

dx

1

1 1;

2 xdx x2

3) функция

–

четная,

поэтому

на основании

0

0

2

(13.14)

b( ) 0;

a( )

f (t) cos tdt

0

2

1

2

1

t

1

t cos tdt

cos

t

sin t

=

2

0

0

2

1

cos

1

sin

1

2

( sin cos 1) .

2

2

2

Данная

функция

является

непрерывной в интервалах

( ; 1) ;

(–1; 1);

(1; ) , кроме того, в точках разрыва среднее арифметиче-

ское односторонних пределов

функции совпадает со значением ее в

этих

точках,

поэтому

можно

записать

интеграл

Фурье

x

,

x

1,

2

sin cos 1

2

cos xd

0,

x

1,

0

1

,

x

1. #

2

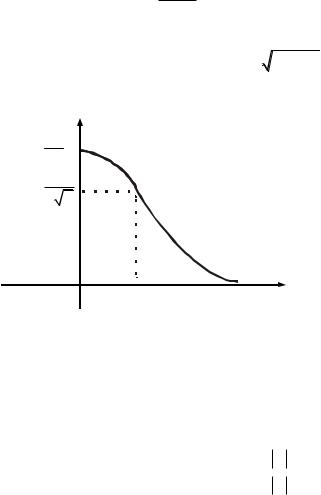
	Пример.				Показать,
				ax		, x 0 ,
ции	f (x)	e
					x 0,
			0,

что спектральной характеристикой функ-

a 0 является функция	1
	c( )		. По-
		a i

строить график спектра f (x) .

Построим график данной функции (рис. 13.5). y

1

0	x
	Рис. 13.5

13.4. Интеграл Фурье. Преобразование Фурье	147

Найдем c( )

e x(a i ) 0

по формуле (13.21) c( )

		1	e x(a i )
	dx
		a i
					0

f (x)e i xdx e axe i xdx

0

1 . a i

Спектр f (x) – это		c(				.		c( )			1							1			.
												a i
																a	2		2
		c( )		(рис. 13.6).
Построим график

| с( ) |

1

а

1

a 2

0

a

Рис. 13.6

Задачи для самостоятельного решения

В задачах функции.

14. f (x)

16. f (x)

14 – 17 представить интегралом Фурье следующие

sgn x,						x						1,
	0,					x						1.
cos x,						x			2				,
												.
	0,					x
										2

15.f (x)

17.f (x)

x, x 1,

0, x 1.

x 2,		2 x 1,
	x,	1 x 1,
	x 2,		1 x 2,
	0,		x		2.

	18.	Функцию f (x) e x , 0 x	представить интегралом
Фурье, продолжая ее: 1) четным образом,			2) нечетным образом на
			cos x
промежуток ( , 0) . Найти значения интегралов					dx и
				1 x2
			0
	x sin x
		dx .
	1 x2
0

148		Г л а в а 13. Ряды Фурье. Интеграл Фурье
19. Используя результат задачи 18, представить интегралами
	f (x)	1			2) f (x)	x
Фурье функции: 1)				;			.
			1 x2			1 x2

20.Написать интеграл Фурье в комплексной форме для функ-

ций: 1) f (x) e a x ; 2) f (x) xe a x , (a 0) .

21.Вычислить спектр прямоугольного импульса высотой h и длительностью и построить график спектра (рис. 13.7).

y

R

				х
	2	2

Рис. 13.7

22. Записать преобразование Фурье для следующих функций:

1) f (t) e		t		;	2) f (t) te		t		.

ОТВЕТЫ К ЗАДАЧАМ ГЛАВЫ 13

1.					sin nx					,	0 x 2 .
									n
	n 1
2.		1				1			cos x		2		1			cos 2x			1	cos 4x ... ( 1)n 1
						2											15
											3
				1												( 1)n n
3.								sin x		2									sin nx .
				2												n2 1
											n 2
								sin(2n 1)x								а)
4.														;			;			б)				.
		n 1							2n 1							4				2		3

	1
				cos 2nx ... .
	2	1
4n

Ответы к задачам главы 13	149

5. а)

в)

г) 2

6

1

( 1)n

4

4

2 4

cos nx ;

б)

2

cos nx

3

n2

3

n2

n 1

n 1

4 ( 1)n 1 2 n2

sin nx ;

n3

n 1

( 1)n

2

n

2

cos nx

(( 1)

1)

sin

n

2

3

n 1

n 1

n

n

4 sin nx ; n

nx .

																				cos(2n 1) x																																		cos					2 n					1						2 nx
	1						4																														2				3
6.																																		.	7.																					3												cos					.
	2								2													(2n 1)									2						3					2																	n	2											3
															n 1																																n 1
																									1 ( 1)n 1 cos 1																		n x
8.	1 cos 1 2																																						cos													.
																												1 n2 2																		2
																				n 1
			e2 1																				1 in													e2 1						1															cos nx											n sin nx
10.																													einx				;																																							.
					2																	1 n					2															2															1 n					2							1 n		2
																																																				n 1
																	1 ( 1)									n 1																						sh													( 1)					n
11.			1																									e					einx .								12.																												einx .
			2																																																										1 n					2
																						1 in
			i sh																							n
13.																						( 1)					n		einx .												14.							2									1 cos										sin xd .
																											2
																						1 n																																0
																																																						cos
			2							sin														cos																								2
																																																																	2
15.																															sin xd .										16.																											cos xd .
																			2																																								1						2
						0																																																0
			4									(1 cos ) sin
17.																																		sin xd .
																									2
							0
								2										cos x																								2										sin x
18.	1)																									d ; x 0 ;													2)																										d ; x 0 ;
																		1 2																																				1 2
												0																																				0

150 Г л а в а 13. Ряды Фурье. Интеграл Фурье

	cos x					x sin x
		dx		;			dx		.
	1 x2		2e			1 x2		2e
0					0
19. 1)	e cos xd ;				2)	e sin xd .

	0																				0
				a							1												2a
20.	1)														ei x d ;						2) i
									a2		2
																						| C( ) |
													sin								h
21.		c( )						h									2
														2							0
22.	1)					2				;	2)			4i								.
				1 2															(1 2 )2

				ei xd .
	a2	2	2

2	3	2

Г Л А В А 14

КРАТНЫЕ, КРИВОЛИНЕЙНЫЕ, ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ

14.1.ОПРЕДЕЛЕНИЕ КРАТНОГО ИНТЕГРАЛА. ОПРЕДЕЛЕНИЕ ДВОЙНОГО И ТРОЙНОГО ИНТЕГРАЛОВ

	Пусть: 1)		в		ограниченной			замкнутой		области	E Rm
x1, x2 , ... xm			«объема» V(E)				задана		ограниченная		функция
f (x1, x2 , ..., x m ) ; 2)				E1, E2 , ..., En – разбиение области							E n Ei
											i 1
										n
на подобласти			Ei	с объемами		Ei		(V (E) Ei ) и диаметрами
									i 1
di ,		sup di
	d			–	диаметр	разбиения;			3)	зафиксируем точки
M ( 1i , i2 , ..., im ) Ei ,					i 1, 2, ..., n ; 4) построим интегральную сумму
					n
					In f (Mi ) Ei .

i 1

Определение. Конечный предел I интегральной суммы In при

d 0 , не зависящий ни от способа разбиения области E, ни от выбора точек Mi , называется m-кратным интегралом от функции f по

области E и обозначается

I ... f (x1, x2 , ..., xm )dE

		E
или
	I ... f (x1, x2 , ..., xm )dx1dx2...dxm .					(14.1)
		E
Таким образом, по определению
					n
I ...	f (x1, x2	, ..., xm )dE lim			f ( 1i , i2 , ..., im ) Ei .	(14.2)
E		n			i 1
		(d 0)

В этом случае функция f (x1, ..., xm ) называется интегрируемой в E.

При m = 2	(m = 3) для ограниченной функции f в замкнутой
области S R2	(x, y)	(V R3 ( x, y, z) ) кратный интеграл
(14.1) называется двойным		(тройным) интегралом, а соответст-