dolgih

182	Г л а в а 14. Кратные, криволинейные, поверхностные интегралы
14.5.2. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ ВТОРОГО РОДА (КИ-2)
	Пусть: 1) в точках непрерывной кривой AB из пространства
R3 {(x, y, z)}		определены ограниченные скалярные функции
P(x,	y, z), Q(x,	y, z), R(x, y, z) ; 2) {l1, l2 , ..., ln} – произвольное

разбиение кривой AB на элементарные дуги li с длинами li и про-

екциями xi xi xi 1 ,	yi yi yi 1 ,		zi zi zi 1 на соответст-
вующие оси координат;	3) Mi ( i , i , i ) li (i 1, 2, ..., n) – произ-
	n
вольный набор точек; 4)	In P( i ,	i , i ) xi Q( i , i , i ) yi
	i 1
R( i , i , i ) zi – интегральная сумма,			соответствующая данному
разбиению и данному выбору точек.

Определение. Конечный предел интегральной суммы In при

sup li , не зависящий ни от способа разбиения AB, ни от выбора точек Mi , называется криволинейным интегралом вто-

рого рода от функций P, Q, R по пути AB:

lim In P(x, y, z)dx Q(x, y, z)dy R(x, y, z)dz .

0

AB

Механически КИ-2 представляет собой работу переменной силы F P, Q, R , точка приложения которой описывает кривую AB.

ВЫЧИСЛЕНИЕ КИ-2

Теорема 14.7. Если линия AB задана в параметрической фор-

ме: x x(t), y y(t), z z(t), t1 t t2 , где x(t), y(t), z(t) – непре-

рывно дифференцируемые функции, и при изменении параметра t от t1 к t2 кривая описывается именно от точки A к точке B, то

P(x, y, z)dx Q(x, y, z)dy R(x, y, z)dz

AB

t2

[P(x(t), y(t), z(t))xt Q(x(t), y(t), z(t)) yt , (14.28)

t1

R(x(t), y(t), z(t))zt ] dt

причем КИ-2 существует, если существует определенный интеграл.

14.5. Криволинейные интегралы	183

Следствия. а) Для плоской линии AB: x x(t),	y y(t), t1 t t2
и функций P(x, y), Q(x, y), (x, y) AB :

		t2		P(x(t), y(t))xt Q(x(t), y(t)) yt dt .
P(x, y)dx Q(x, y)dy
AB		t1
б) Для заданной явно плоской линии AB : y y(x), a x b
		b
	P(x, y)dx Q(x, y)dy		[P(x, y(x)) Q(x, y(x)) y ]dx . (14.29)
				x
AB		a

НЕЗАВИСИМОСТЬ КИ-2 ОТ ПУТИ ИНТЕГРИРОВАНИЯ

Теорема 14.8. Если функции P(x, y, z), Q(x, y, z), R(x, y, z)

непрерывны вместе со своими частными производными первого порядка в некоторой замкнутой ограниченной поверхностно односвязной области V, то равносильны следующие четыре утверждения:

1) тPdx + Qdy + Rdz = 0 , где l – замкнутый контур, лежащий

l

внутри V;

2) Pdx Qdy Rdz не зависит от выбора пути интегрирования;

l

3) Pdx qdy Rdz есть полный дифференциал некоторой од-

нозначной функции (x, y, z) , заданной в точках V;
4) выполняются равенства: P			Q ,	P	R ,	R	Q .
		y	x	z	x	y	z
Функция (x, y, z) может быть найдена, например, по формуле
	( x, y,z )	x		y
(x, y, z)		d (x, y, z) P(x, y, z)dx Q(x0 , y, z)dy
	( x0 , y0 ,z0 )	x0		y0

z

(14.30)

R(x0 , y0 , z)dz c ,

z0

где (x0 , y0 , z0 ) – некоторая фиксированная точка области V, c – произвольная постоянная.

СВЯЗЬ МЕЖДУ КИ-1 И КИ-2

Пусть спрямляемая (не имеющая особых точек) линия AB имеет в каждой точке касательную, положительное направление которой составляет с осями координат углы , , . Тогда

Pdx Qdy Rdz (P cos Q cos R cos )dl .

AB

AB

184	Г л а в а 14. Кратные, криволинейные, поверхностные интегралы

СВЯЗЬ КИ-2 С ДВОЙНЫМ ИНТЕГРАЛОМ (ФОРМУЛА ГРИНА)

Теорема 14.9. Пусть: 1) функции P(x, y), Q(x, y) непрерывны и имеют непрерывные частные производные в открытой односвязной области G Oxy ; 2) l – кусочно-гладкий контур, ограничиваю-

щий область S G ,	и при положительном обходе l ближайшая
часть области S находится слева от наблюдателя. Тогда справедлива
формула
			Q		P
Pdx Qdy			x		dxdy .
l	S				y

Площадь плоской области. Площадь s фигуры S, ограни-

ченной простым кусочно-гладким контуром l, равна

	s	xdy	ydx	1		xdy ydx .
				2
	l	l			l
	Пример 20. Вычислить КИ-2				I ydx ( y x2 )dy , где L –
						l

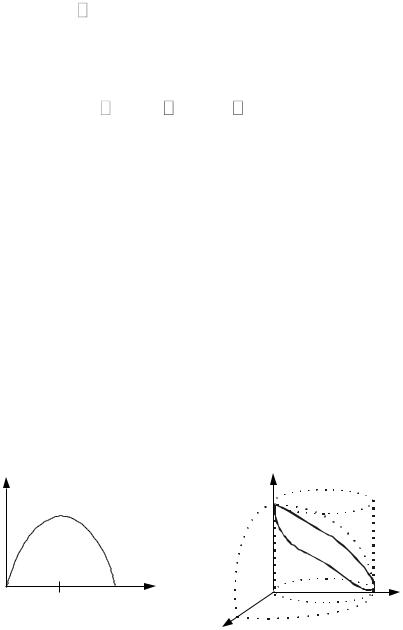
дуга параболы y 2x x2 , проходимая от точки A(2; 0) до точки

O(0; 0) .

Кривая l представлена на рис. 14.24. По формуле (14.29) име-

ем I ydx ( y x2 )dy			xO 0
				(2x x2 )dx (2x x 2 x 2)(2 2x)dx
l			xA 2
= ( x2 x3 )		0 4 .
		2
Пример 21. Вычислить КИ-2 I ydx xdy zdz, где l –
				l

замкнутый контур, полученный пересечением сферы x2 y2 z2 R2

и цилиндра x2 y2 Ry (R 0, z 0) , обходимый против часовой стрелки, если смотреть из начала координат (рис. 14.25).

	у			z
	1
				A
	0	1	2	0
				y
				x
		Рис. 14.24		Рис. 14.25

l

A(0; 0), B(2; 0), C(4; 4), D(0; 4) , указанными в порядке обхода l.

98.

14.5. Криволинейные интегралы	185

Для вычисления КИ-2 представим l в параметрической

форме.

Поверхность x2 y2 Ry запишем в виде x2

( y R / 2)2

(R / 2)2 .

Последнее

равенство

выполнится

тождественно,

если

положить,

например,

x (R /

2) sin t ,

y (R / 2)(1 cos t) ,

0 t 2 .

Тогда

из уравнения

сферы

имеем

z2

R2

x2

y2 =

= R2 (R2

/ 4) sin2

t (R2

/ 4)(1 cos t)2 (R2

/ 2)(1 cos t) = R2 sin2 (t / 2) .

Отсюда,

помня,

что z 0,

0 t 2 ,

имеем

z R sin(t / 2) .

Итак,

l : x

R

sin t,

y

R

(1 cos t),

z R sin

t

, t [0;

2 ] ;

x

R

cos t ,

2

2

2

t

2

yt

R

sin t ,

zt

R

cos

t

. По формуле (14.28)

I ydx xdy zdz

2

2

2

l

2

R

R

R

R

t R

t

=

(1 cos t)

cos t

sin t

sin t

R sin

cos

dt

0

2

2

2

2

2 2

2

R

2

2

R

2

02

R

2

=

(1 cos t sin t)dt

(t sin t cos t)

.

4

4

2

0

Пример 22.

Найти первообразную функции

u(x, y, z) , если

du (6x 7 yz)dx (6y 7xz)dy (6z 7xy)dz .

По формуле (14.30) при xo yo				zo 0 получим
x			y			z
u(x, y, z) (6x 7 yz)dx				6 ydy 6zdz c
0			0	0
(3x2 7xyz)		x x	3 y2			y 3z 2		z c
		x 0				0		0

3(x2 y2 z2 ) 7xyz c .

Задачи для самостоятельного решения

Вычислить криволинейные интегралы второго рода.

97. xdy , где l – отрезок прямой	x / a y / b 1 от точки пе-
l

ресечения ее с осью Ox до точки пересечения с осью Oy.

(x2 y2 )dy , где l – контур четырехугольника с вершинами

186	Г л а в а 14. Кратные, криволинейные, поверхностные интегралы
	(1;1)
99.			xydx ( y x)dy вдоль линий:				1) y x , 2) y x2 ,
	(0;0)
3) y2 x , 4) y x3 .
100.			ydx xdy , l – эллипс x a cos t, y b sin t , обходимый
		l
в положительном направлении.
101.		(2a y)dx (a y)dy , где l – первая от начала координат
		l
арка циклоиды x a(t sin t) , y a(1 cos t) .
102.		xdx ydy (x y 1)dz , где l – отрезок прямой от точки
		l
(1; 1; 1) до точки (2; 3; 4).
103.		yzdx zxdy xydz ,		где	l	–	дуга винтовой	линии
		l
x R cos t, y R sin t, z at /				(0 t 2 ) .
104.			y2dx z2dy x2dz ,	где l	–	линия пересечения		сферы
		l
x2 y2	z2 R2 и цилиндра x2			y2	Rx		( R 0, z 0 ), обходимая

против часовой стрелки, если смотреть из начала координат (часть кривой Вивиани).

Убедиться, что подынтегральное выражение является полным дифференциалом, и вычислить КИ-2.

	(2; 1)			(5;12)	xdx ydy
		2xydx x2dy .
105.			106.				.
					x2 y2
	(0; 0)			(3; 4)
	(3; 2;1)			(5; 3; 1)		zxdy xydz yzdx
107.		yzdx zxdy xydz .	108.							(кон-
						(x yz)			2
	(1; 2;3)			(7; 2; 3)
турное интегрирование не пересекает поверхность								z x / y) .

Найти первообразную функцию и по полному дифференциалу.

109.du 4(x2 y2 )(xdx ydy) .

110.du (2x cos y y2 sin x)dx (2y cos x x2 sin y)dy .

111.du

112.du

	2x(1 e	y	)		e	y
				dx			1 dy .
	(1 x2 )2				1 x2

(x2 2yz)dx ( y2 2xz)dy (z2 2xy)dz .

14.6. Поверхностные интегралы

187

dx dy dz

1

y

x

x

xy

113.

du

.

114. du 1

dx

dy

dz.

x y z

y

z

z

y

2

z

2

С помощью формулы Грина вычислить КИ-2.

115.

Сxy2dy - x2 ydx , где l – окружность x2 y2

R2 .

т

l

116.

С(x + y)dx -

(x -

y)dy , где l – эллипс x2

/ a2 y2

/ b2 1.

т

l

117.

Вычислить

Сxdy - ydx , где l –

простой замкнутый кон-

т

l

тур, пробегаемый в положительном направлении.

У к а з а н и е. Рассмотреть случаи: 1) начало координат находится вне контура l; 2) контур l окружает начало координат.

118. В каждой точке эллипса x2 / a2 y2 / b2 1 приложена сила F , равная по величине расстоянию от точки M до центра эллипса и направленная к центру эллипса. Найти работу F при перемещении в положительном направлении: а) вдоль дуги эллипса в первом октанте; б) вдоль всего эллипса.

119. Сила по величине обратно пропорциональна расстоянию точки ее приложения от оси Oz , перпендикулярна к этой оси и на-

правлена к ней.

Найти

работу

этой

силы по окружности

x cos t, y 1, z sin t от точки M (1; 1; 0) до точки N(0; 1; 1) .

kx

ky

У к а з а н и е. F

,

,

0

.

x2 y2

x2

y2

14.6. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ

14.6.1. ДВУСТОРОННИЕ ПОВЕРХНОСТИ И ИХ ОРИЕНТАЦИЯ

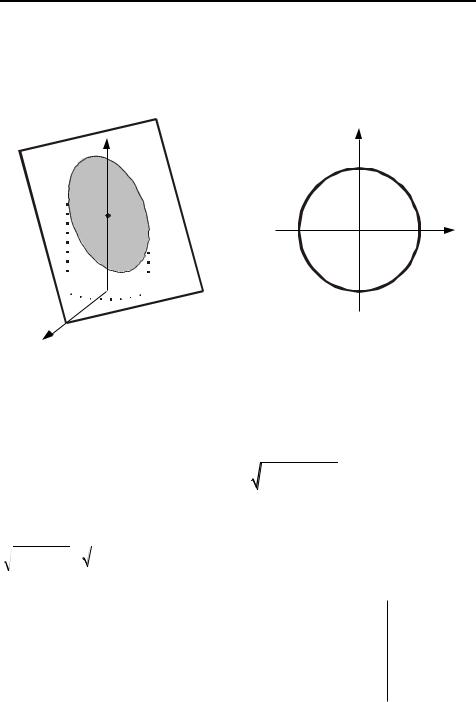
Гладкая поверхность называется двусторонней поверхностью, если при возвращении в исходную точку после обхода замкнутого контура, лежащего на и не имеющего общих точек с ее границей, направление нормали к поверхности не меняется.

Совокупность всех точек поверхности с приписанными в них по указанному правилу нормалями называется определенной стороной поверхности.

Выбор определенной стороны поверхности называется ориентацией поверхности. Выбранная сторона – это положительная сторона поверхности. Для замкнутой поверхности положительной считается внешняя сторона.

188

Г л а в а 14. Кратные, криволинейные, поверхностные интегралы

Если задана неявным уравнением

F(x, y, z) 0 , то сторона

характеризуется одним из единичных нормальных векторов

, n Fx , Fy , Fz ,

n

n /

n

n

Fx 2 Fy 2 Fz 2 . (14.31)

Если задана явным уравнением z z(x, y) , (x, y) Sxy , то сторона характеризуется одним из векторов n o :

, n { z

z

n n /

n

,

, 1} ,

n

1 z 2

z 2 .

(14.32)

x

y

x

y

14.6.2. ПОВЕРХНОСТНЫЙ ИНТЕГРАЛ ПЕРВОГО РОДА (ПИ-1)

Пусть: 1) в точках двусторонней гладкой (или кусочногладкой) поверхности из пространства R3 x, y, z , ограниченной кусочно-гладким контуром, определена ограниченная ска-

лярная функция	f (x, y, z) ;		2) 1, 2 , ...,	n – произвольное раз-
биение на n	частей i		с площадями	i и диаметрами di ;
3) Mi ( i , i , i ) i		(i 1, 2, .., n) – произвольный набор точек;
n
4) In f ( i , i , i ) i –			интегральная сумма, соответствующая
i 1
данному разбиению поверхности и выбору точек Mi .
Определение. Конечный предел интегральной суммы In при

0 ( sup di ) , не зависящий ни от способа разбиения поверхности , ни от выбора точек Mi , называется поверхностным интегралом первого рода от функции f (x, y, z) по поверхности :

lim In f (x, y, z)d .

n

ВЫЧИСЛЕНИЕ ПИ-1

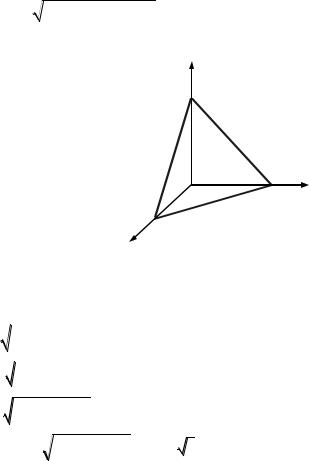
Теорема 14.10. Если: 1) поверхность задана неявным уравнением F(x, y, z) 0 и z z(x, y) есть решение этого уравнения

при (x, y) Sxy или y y(x, z) – решение уравнения при ( y, z) Syz , или x x( y, z) – решение уравнения при ( y, z) Syz , где Sxy , Sxz , Syz

– проекции на плоскости Oxy, Oxz, Oyz соответственно; 2) между

точками и ее соответствующей проекцией установлено взаимно однозначное соответствие, то

14.6. Поверхностные интегралы	189

f (x, y,, z)d f (x, y,

Sxy

f (x, y(x, z), z)

Sxz

f (x( y, z), y, z)

S yz

z(x, y)) dxdy cos

		dxdz					,
		cos
		dydz					(14.33)
	cos

причем ПИ-1 существует, если существуют соответствующие двой-

ные интегралы. Здесь cos , cos , cos – координаты вектора n и находятся по формулам (14.31). ПИ-1 не зависит от выбора стороны поверхности.

Следствие. При явном задании : z z(x, y), (x, y) Sxy в си-

лу (14.32) из (14.33) получим

						x	y
		f (x,	y, z)d		f (x, y, z(x, y)) 1 z 2		z 2 dxdy		(14.34)
				Sxy
			НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ПИ-1
1. Масса			материальной поверхности. Пусть (x, y, z) –

поверхностная плотность материальной поверхности площади s. Тогда масса этой поверхности m (x, y, z)d .

2. Площадь искривленной поверхности . Если принять в пре-

дыдущей формуле (x, y, z) 1, то масса поверхности численно

равна площади s , т.е. s d .

3. Статические моменты материальной поверхности с по-

верхностной	плотностью	(x, y, z)	и	массой	m относительно
плоскостей	Oxy, Oxz, Oyz	соответственно		равны:	M xy zd ,
M xz yd , M yz xd .
4. Координаты центра тяжести материальной поверхности :
	xc M yz / m, y M xz / m,		zc M xy / m .

Задания. 1. Записать линейные свойства ПИ-1.

2. Записать свойство аддитивности для ПИ-1.

190	Г л а в а 14. Кратные, криволинейные, поверхностные интегралы
	Пример 23. Вычислить ПИ-1 I zd , где – часть плоско-
сти	x / a y / b z / c 1, вырезанная цилиндром		x2 y2 R2
(рис. 14.26).
	z	y
	C	-R	R
		o
			x

о b y

x a

Рис. 14.26

Поверхность проектируется на плоскость Oxy в круг

S : x2 y2 R2 . По формуле (14.34)

					x	y
I		zd		z(x, y) 1 z 2		z 2 dxdy .

S

Из уравнения следует:	z c(1 x / a y / b) ,	z	c / a,	z	c / b,
		x		y

1 zx2 zy2

=

				I ck (1 x / a
	1 c2 / a2 c2 / b2 k ; тогда
				S
	переходим к полярным координатам:
				0	2 ,
	x cos , , y sin , S P :				R
				0
	dxdy d d , x2 y2 R2			R,

y / b)dxdy

=

		1		1
= ck 1			cos		sin	d d
P		a		b

R	2		1		1
= ck	d 1			cos		sin d
0	0		a		b

14.6. Поверхностные интегралы	191

R

1

1

2

= ck d (

sin

cos )

0

a

b

0

R

2 c k d R2c 1 c2 / a2 c2 / b2 .

0

Пример

24. Вычислить ПИ-1

z

I xd , где – полная поверхность

1

C

тетраэдра, отсекаемого от первого ок-

танта плоскостью x y z 1.

Полная поверхность

тетра-

эдра складывается из его граней:

o

1 2 3 4 ,

A

где

1

AOB, 2 AOC, 3 BOC,

1

4 ABC (рис. 14.27).

x

Рис. 14.27

Выпишем

уравнения

поверхно-

стей

i

и вычислим для них элемен-

ты d :

а)

: z 0,

d

1 z 2

z 2 dxdy dxdy ;

1

x

y

б)

2

: y 0,

d

1 y 2 y 2 dxdz dxdz

;

x

z

в)

: x 0,

d

1 x 2

x 2 dydz dydz ;

3

y

z

: x 1 z y, d

1 x 2 x 2 dydz

г)

4

3dydz .

y

z

B

1 y

Задав уравнения поверхностей в явном виде, мы определили тем самым плоскости проектирования их; Di – области, на которые проек-

тируются i .

I xd
	1	2	3 4

xdydx xdxdz 0dydz (1 y z) dydz .

D1 D2 D3 D4

По поводу последней записи напомним, что следует в подынтегральной функции f (x, y, z) независимые переменные (переменные из об-

ласти Di ) оставлять без изменения, зависимую переменную заме-

нить из явного уравнения соответствующей поверхности, а d заменить выражением, полученным выше, причем D3 D4 .