dolgih

36 Г л а в а 10. Обыкновенные дифференциальные уравнения

Найти частное решение, удовлетворяющее условию y(1) 1 (найти интегральную кривую, проходящую через точку M0 (1; 1) ).

Производная	y 3Cx2 . Подставляя y и y		в уравнение, по-
лучаем тождество	3Cx3 3Cx3 0 .	Это означает, что функция
y Cx3 является решением данного		уравнения.	Положив в нем

x 1, y 1, найдем значение параметра C: 1 C 13 C 1 . Подставив C = 1 в решение, получим частное решение y x3 : интегральной кривой, проходящей через точку M0 (1; 1) является кубическая парабола y x3 . #

10.3. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА В НОРМАЛЬНОЙ ИЛИ ДИФФЕРЕНЦИАЛЬНОЙ ФОРМАХ, РЕШАЕМЫЕ В КВАДРАТУРАХ

10.3.1. УРАВНЕНИЯ С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ

Уравнение (10.4) или (10.5) называется уравнением с разделяющимися переменными, если функция f (x, y) или коэффициенты

M (x, y) , N (x, y) могут быть разложены на множители, каждый из

которых зависит только от одной переменной:								f (x, y) f1(x) f2 ( y)
или	M (x, y) M1(x) M2 ( y) , N(x, y) N1(x) N2 ( y) .									Путем деления
на	f2 ( y) и на M2 ( y)N1(x)			эти уравнения приводятся соответствен-
но к виду
	f1(x)dx		1	dy,	M1(x)	dx	N2	( y)	dy	(10.8)
		f2	( y)		N1(x)		M2	( y)

– к уравнениям с разделенными переменными. При этом уравнения

(10.4) и (10.5) имеют также решения y y0 и		x x0 , если	y0 , x0 –
корни знаменателей f2 ( y)	или M2 ( y) , N1(x) .
Теорема. Общим интегралом дифференциального уравнения с
разделенными переменными
X (x)dx Y (y)dy 0			(10.9)
является
X (x)dx Y ( y)dy C ,			(10.10)
или
x	y
X (x)dx Y ( y)dy C .			(10.11)
x0	y0

Особых решений нет.

10.3. Уравнения первого порядка, решаемые в квадратурах

37

Пример 1. Решить уравнение x2 y2 y 1 y .

Приводим уравнение к виду (10.8). Имеем:

x2 y

2 dy

y 1;

dx

x2 y2dy ( y 1)dx . Делим обе части уравнения на x2 ( y 1) :

y2

dy

y 1

dx

–

приходим

к уравнению с

разделенными

переменными.

x2

Интегрируем обе части уравнения [применяем формулу (10.10)]:

y2

dx

y2

1

dy

С;

y ln

y 1

C .

При делении

на

y 1

x2

2

x

x2 ( y 1) могли быть потеряны решения

x 0

и y 1.

Очевидно,

y 1– решение уравнения (частное), а x 0 – нет. #

З а м е ч а н и е. Уравнение вида

y f (ax by с)

приводится

к

уравнению

с

разделяющимися

переменными

подстановкой

z ax by с (при этом z a by ).

Пример 2. Найти частное решение уравнения

(1 ex ) yy ex ,

удовлетворяющее начальному условию y(0)=1.

Имеем

(1 ex ) y

dy

ex .

Разделяя

переменные,

полу-

dx

чаем

ydy

exdx

.

Интегрируя,

находим

общий

интеграл

1 ex

y2

ln(1 ex ) C .

Полагая

в

нем

x = 0,

y = 1,

будем

иметь

2

1

ln 2 С ,

откуда

С 1/ 2 ln 2 . Подставляя в общий интеграл

2

найденное

значение

С,

получаем

частное

решение:

1 ex 2

1 ex 2

y2 1 ln

,

откуда

y

1 ln

. Из начального ус-

2

2

ловия следует, что

y 0, ( y(0) 1 0) , поэтому перед корнем берем

знак плюс; искомое частное решение:

y

1 ln

(1 ex ) / 2 2 . #

Пример 3.

Проинтегрировать уравнение

2 y

by y2 dx

(b2 x2 )dy 0

и выделить интегральную кривую, проходящую че-

рез точку (0; b).

Разделяем переменные в уравнении и интегрируем:

2dx

dy

x

b y

0

y by y2 0? , arctg

C

(*).

b

2

x

2

b

y

y

by y2

Далее из

y

by y2

0

находим решения уравнения: y = 0, y = b.

38	Г л а в а 10. Обыкновенные дифференциальные уравнения

Первое из этих решений частное, второе – особое, так как для любого x0 через точку (x0 ,b) , кроме решения y b , проходит также ре-

	шение, получаемое из общего интеграла при C arctg			x0			. Полагая в
				b
	общем интеграле (*) x 0, y b , находим C = 0, так что через за-
	данную точку проходит интегральная кривая arctg	x					b y		0 и,
		b					y

кроме того, y b . #

10.3.2.ОДНОРОДНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

ИПРИВОДЯЩИЕСЯ К НИМ

1 . Однородные уравнения

Уравнения (10.4) или (10.5) называются однородными, если f (x, y) есть однородная функция нулевого измерения:

f (tx, ty) f (x, y) ,

(10.12)

или функции M (x, y) и N (x, y) являются однородными одного измерения:

M (tx, ty) tmM (x, y) ,

N(tx, ty) t mN (x, y) .

(10.13)

Однородное уравнение (10.4) всегда можно представить в виде

y
y			.
x
Любой из подстановок: y u(x)x или			x t( y) y

(10.14)

– однородное урав-

нение сводится к уравнению с разделяющимися переменными. На-

	пример, вводя новую искомую функцию				u	y	(т.е. y ux ,
						x
	y u x u ), сведем (10.14) к уравнению
	x	du	(u) u	,			(10.15)
		dx
	в котором переменные разделяются. Если			u u0 есть корень урав-

нения (u) u 0 , то уравнение (10.14) будет также иметь решение y u0 x (прямая, проходящая через начало координат).

З а м е ч а н и е. При решении однородных уравнений не обязательно приводить их к виду (10.14). Можно сразу выполнять под-

становку y ux (или x ty) .
Пример 1. Решить уравнение xy	x2 y2 y .

Имеем однородное уравнение (заменяя в уравнении x и y на

tx, ty, приходим к исходному уравнению: tx y 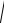(tx)2 (ty)2 ty xy

10.3. Уравнения первого порядка, решаемые в квадратурах	39

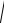x2

xy

y2	y ; иначе, уравнение приводится к виду y
		y
y				. Положим	y ux , тогда	y u x u
	x

	y 2
1
x

, подставим

du

в уравнение,

получим:

x

1 u2 . Разделим

переменные:

dx

du

dx

. Отсюда

интегрированием

функций находим

x

1 u2

arcsin u ln

x

ln C или arcsin u ln

xC

. Подставляя

u

y

, по-

y x sin ln

x

сле преобразования получаем общее решение

C x

. При

разделении переменных обе части уравнения делили на произведе-

ние x1 u2 , поэтому могли потерять решения, которые обращают в

нуль это произведение. Положим 1 u2 0 ( x 0 –			см. область
определения уравнения). Из этого уравнения находим			y x . Про-

верка показывает, что и y x и y x – решения данного уравнения (особые, так как через каждую точку (x0 , x0 ) проходит также

	решение, получаемое из общего решения при C	e / 2		; графики
		x0
	особых решений лежат на границе области определения. #
	Пример 2. Проинтегрировать уравнение (x2 2xy y2 )dx
	+ ( y2 2xy x2 )dy 0 и выделить интегральную кривую,			проходя-

щую через точки: а) (2; 2); б) (1; –1); в) (0; 0).

Записав уравнение в форме (10.4) и (10.4 ), заметим, что условия теоремы существования и единственности решения не выполнены лишь в точке (0,0), принадлежащей, однако, области опреде-

ления уравнения.

Положим y ux . Тогда

dy xdu udx , так что

(x2 2ux2

u2 x2 )dx (u2 x2 2x2u x2 )(xdu udx) 0 .

Разделим пе-

ременные:

dx

u2 2u 1

du 0

( u 1 0

?, x 0

не является

x

(u2 1)(u 1)

решением

уравнения).

Интегрируя,

получаем ln

x

ln

u 1

ln(u2 1) ln

C

или

x(u2 1)

C (C C )

. Заменив здесь u на

1

u 1

1

y

x2 y2

C . Это есть

, получим общий интеграл уравнения в виде

x

x y

семейство окружностей

x2 y2 C(x y) ,

проходящих через нача-

40 Г л а в а 10. Обыкновенные дифференциальные уравнения

ло координат, с центрами на прямой y x , из которых нужно ис-

ключить	начало координат; это частные	решения. Полупрямые
x y 0	(x 0) , определяемые равенством	u 1 0 , также соответ-

ствуют частным решениям уравнения. Решим поставленную задачу

Коши: а) полагая в x2 y2			C(x y) x 2, y 2 , находим С = 2,
так что искомое решение:			x2 y2	2(x y) . Решение	x y 0 не
проходит через		точку (2,	2);	б) ни одна из	окружностей
x2 y2	C(x y)	не проходит через точку (1; –1), зато полупрямая
y x	(0 x ) проходит через эту точку и дает искомое реше-

ние; в) через точку (0,0) проходят все вышеуказанные решения, продолженные по непрерывности. Решение задачи Коши не единственно.#

2 . Уравнения, приводящиеся к однородным. Дифференци-

	альные уравнения вида
					y		a x b y с
						f	1	1	1		(10.16)
						a2 x b2 y с2
	в случае	a2		b2	приводятся к однородным уравнениям с помощью
		a1		b1

замены переменных x u m, y v n , где m и n находятся из сис-

	темы уравнений a1m b1n с1 0,			a2m b2n с2						0 .
	Если в уравнении (10.16)				a2			b2		и, следовательно,
					a1			b1
	a2 x b2 y (a1x b1 y) , то оно примет вид
		a1x b1 y		с1
	y f						(a1x b1 y) .
		a x b y		с
		1	1	2
	Подстановкой u a1x b1 y		это уравнение преобразуется к уравне-
	нию с разделяющимися переменными (см. замечание в п. 10.3.1).
	Пример 3. Решить уравнение (x y 2)dx (x y 4)dy 0 .
	Система m n 2 0; m n 4 0 имеет единственное реше-
	ние m 1, n 3 . Замена		x u 1, y v 3 приводит уравнение к

виду (u v)du (u v)dv 0 – это однородное уравнение. Полагаем

v tu , получим

(u ut)du (u ut)(udt tdu) ,

откуда (1 2t t2 )du

u(1 t)dt 0 .

Разделяем переменные:

du

(1 t)dt

0 . Интегри-

u

1 2t t2

1

ln C , или

u2

(1 2t t2 ) C . Возвра-

руя, находим ln

u

ln

1 2t t2

2

щаясь к «старым переменным» x и y, получаем

10.3. Уравнения первого порядка, решаемые в квадратурах								41
		y 3			( y 3)2
(x 1)2 1 2							C
		x 1			(x 1)2		1
или
x2 2xy y2 4x 8y C (C C 14) . #
							1
Пример 4. Решить уравнение (x y 1)dx (2x 2y 1)dy 0 .
Система m n 1 0,	2m 2n 1 0 несовместна. Для интег-
рирования уравнения применяем				подстановку u x y, dy du dx .

Уравнение примет вид (2 u)dx (2u 1)du 0 – уравнение с разделяющимися переменными. Разделяя переменные, получаем:

	dx	2u 1	du 0 , откуда	x 2u 3ln		u 2		C . Возвращаясь к пере-
		u 2

менным x, y, получаем общий интеграл данного уравнения: x 2y 3ln x y 2 C . #

10.3.3.ЛИНЕЙНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА. УРАВНЕНИЕ БЕРНУЛЛИ

1 . Линейные уравнения. Линейным дифференциальным урав-

нением называется линейное относительно неизвестной функции и ее производной уравнение:

y p(x) y f (x) ,					(10.17)
где p(x) и f (x) – заданные непрерывные функции от					x (a, b) .
Через каждую точку (x0 , y0 ) полосы a x b ,		y			проходит

одна и только одна интегральная кривая уравнения (10.17), определенная во всем интервале (a, b) . Всякое решение линейного уравнения есть частное, так что особых решений оно не имеет.

Если f (x) 0 , то уравнение (10.17) называется линейным од-

нородным:

y p(x) y 0 .

(10.18)

Оно является уравнением с разделяющимися переменными и имеет общее решение

y Ce	p( x)dx	.	(10.19)

Все решения линейного однородного уравнения (10.18) содержатся в формуле (10.19) его общего решения. Общее решение неоднородного линейного уравнения (10.17) может быть найдено несколькими способами; здесь рассмотрим два из них.

А. Метод подстановки (метод Бернулли). Положим y(x) u(x)v(x) . Тогда уравнение (10.17) приводится к виду

u v uv p(x)uv f (x) .

(10.20)

42 Г л а в а 10. Обыкновенные дифференциальные уравнения

Выберем функции u(x) и v(x) так,	чтобы сумма uv puv обрати-
лась в ноль. Так как u(x) не равна тождественно нулю [ y 0 не яв-
ляется решением уравнения (10.17)],	то должно быть

v pv 0

(10.21)

– для определения функции v(x) получили уравнение с разделяющимися переменными. Выбрав какое-либо частное решение v(x) ,

подставим его в (10.20); для определения функции	u(x) получим
уравнение с разделяющимися переменными
u v(x) f (x) .	(10.22)

Решая уравнение (10.22), найдем его общее решение u u(x, c) . Пе-

ремножая найденные функции

v(x)

и u(x, c) , получаем общее ре-

шение уравнения (10.17):

y(x) v(x)u(x, c) .

Пример 1. Решить уравнение

x(x 1) y y x2 (2x 1) . Выде-

лить частное решение, проходящее через точку M0 (2; 4) .

Ищем общее решение уравнения в

виде

y uv .

Подстав-

ляя y uv

и y u v uv

в уравнение,

получим:

x(x 1)(u v uv )

+

uv x2 (2x 1) , или

x(x 1)vu [x(x 1)v v]u x2 (2x 1) .

( )

*

Функцию

v v(x)

найдем

из

условия

x(x 1)v v 0:

x(x 1)

dv

v ,

dv

dx

.

dx

v

x(x 1)

1

x (x 1)

1

1

Интегрируем уравнение

:

x(x 1)

x(x 1)

x

1 x

ln

v

ln

x 1

ln

x

ln C . Возьмем частное решение

v

x

.

x 1

u 2x 1,

Подставляя его в (*), получаем уравнение

из которого

интегрированием находим функцию

u(x):

u(x) x2 x C . Общее

решение исходного уравнения y [ y uv]

Cx

x2 .

x 1

Чтобы выделить нужную интегральную кривую, подставим в

найденное

решение

x 2, y 4 : 4 С

2

22 ,

откуда

С =

0;

2

1

решением поставленной задачи Коши служит парабола y x2 . #

10.3. Уравнения первого порядка, решаемые в квадратурах

43

Пример 2.

Решить уравнение y

y2

.

2xy 3

Перепишем уравнение в виде

dx

2

x

3

– оно линей-

dy

y

y2

но относительно x

и

dx

.

Решим его методом подстановки.

Пола-

dy

гаем

x uv ,

тогда

x u v uv

и

после

подстановки

x

и

x

2v

3

в уравнение,

оно

приводится к

виду:

u v u v

(*).

2

y

y

Функцию v v( y)

определяем из уравнения

dv

2v

0 . Из его об-

dy

y

щего

решения

v y2 C

выберем,

например,

частное

решение

v y2

и подставим его в (*); получим

du

y2

3

или

du

3

.

dy

y2

dy

y4

Общее решение

этого уравнения:

u( y, C) C

1

.

Перемножая

y3

v( y) и

u( y, C) ,

получим

общее

решение

данного

уравнения

x Cy2 1y . #

Б. Метод вариации произвольной постоянной (метод Лагран-

жа). По этому методу решение уравнения (10.17) ищут в виде (10.19), т.е. в том же виде, в котором найдено решение соответствующего ему однородного уравнения (10.18), считая в этой записи С

некоторой подлежащей определению функцией	переменной x:
С С(x) . Для определения C(x) составляют уравнение
C (x)e p( x)dx f (x)	(10.23)
– уравнение с разделяющимися переменными.

Пример 3. Проинтегрировать уравнение y 2xy 2xe x2 .

1. Решим соответствующее исходному неоднородному уравнению однородное линейное уравнение: y 2xy 0 . Это уравнение с разделяющимися переменными. Его общее решение имеет вид:

y Ce x2 . 2. Ищем общее решение линейного неоднородного урав-

нения в виде y C(x)e x2 , где С С(x) – подлежащая определению

неизвестная функция от x. Подставляя			y e p( x)dx e x2 в (10.23),
			1
для	определения C(x) получаем уравнение С 2x , откуда
C(x) x2 C . Итак, общее решение			неоднородного уравнения
y	x2 C	. #
	ex2

44	Г л а в а 10. Обыкновенные дифференциальные уравнения
	2 . Уравнение Бернулли. Уравнением Бернулли называется
уравнение
	y p(x)y f (x)y n ,	(10.24)

где n 0; 1 (при n = 0 имеем линейное, а при n = 1 – уравнение с

разделяющимися переменными). Интегрируется уравнение Бернулли как и линейное.

З а м е ч а н и е. При n 1 уравнение Бернулли имеет решение y 0 .

Пример. Проинтегрировать уравнение y 2xy 2x3 y2 и найти интегральную кривую, проходящую через точку M0 (0; 1) .

Заметим, что это уравнение

имеет решение y 0 . Полагаем

далее,

y uv . Подставляя

y uv и

y u v uv в уравнение, полу-

чаем: u v u(v 2xv) 2x3u2v2

(*). Из v 2xv 0 по разделении пе-

ременных:

dv

2xdx находим

v Cex2 . Возьмем v ex2 и подста-

v

вим

в (*);

получим

уравнение

u 2x3ex2 u2 . Проинтегри-

руем

его

du

2x3ex2 dx ,

1

x2ex2 dx2 C ,

1

ex2 (x2 1) C

2

u

u

u

и

1

x2 1 Ce x2 . Следовательно,

общим решением уравнения

y

будет

y

1

. Решение

y = 0 – частное решение. Через

Ce x2 1 x2

1

точку (0; 1) проходит кривая y

. #

1 x2

10.3.4.УРАВНЕНИЯ В ПОЛНЫХ ДИФФЕРЕНЦИАЛАХ. ИНТЕГРИРУЮЩИЙ МНОЖИТЕЛЬ

1 . Уравнения в полных дифференциалах. Уравнение (10.5)

называется уравнением в полных дифференциалах, если его левая часть есть полный дифференциал некоторой (однозначной) функции u u(x, y) :

M (x, y)dx N (x, y)dy du	u dx	u dy .	(10.25)
	x	y

С учетом (10.25) уравнение в полных дифференциалах может быть переписано в виде

du 0 ,	(10.26)
так что его общий интеграл имеет вид
u(x, y) C .	(10.27)

10.3. Уравнения первого порядка, решаемые в квадратурах	45

Теорема, приведенная ниже, позволяет установить, является ли уравнение (10.5) уравнением (10.26) – уравнением в полных дифференциалах.

Теорема. Пусть функции M (x, y) и N (x, y) определены и непрерывны в некоторой односвязной области D и имеют в ней непрерывные частные производные соответственно по y и по x. Тогда для того чтобы уравнение (10.5) было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось тождество

M		N .	(10.28)
y		x

При выполнении условия (10.28) общий интеграл можно записать в виде

x	y
	M (x, y)dx	N (x0 , y)dy C ,		(10.29)
x0	y0
или
x		y
	M (x, y0 )dx		N (x, y)dy C ,	(10.30)
x0		y0

где нижние пределы x0 , y0 можно выбирать произвольно, лишь бы точка (x0 , y0 ) D . Особых решений уравнение в полных дифферен-

циалах не имеет.

Пример 1. Проинтегрировать уравнение (sin xy xy cos xy)dx

x2 cos xydy 0 .

Проверим выполнение условия (10.28) – является ли оно уравнением в полных дифференциалах? Имеем:

	M					(sin xy xy cos xy) 2x cos xy x2 y sin xy;
		y
					y
N				(x2 cos xy) 2x cos xy x2 y sin xy ,
x		x
так что M					N – имеем уравнение в полных дифференциалах.
				y		x
	Общее решение определим по формуле (10.30), взяв за началь-
							x	y
ную точку M0 (0, 0) :							(sin x 0 x 0 cos x 0)dx x2 cos xydy C ;
							0	0
отсюда x sin xy C							есть общий интеграл данного дифференциаль-

ного уравнения. # Укажем другой способ нахождения общего интеграла уравне-

ния в полных дифференциалах.