
Прикладные пакеты моделирования (2 лаб)
.pdfФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ Федеральное государственное образовательное бюджетное учреждение
высшего профессионального образования «Санкт-Петербургский государственный университет телекоммуникаций
им. проф. М. А. Бонч-Бруевича»
_____________________________________________________________________________
Кафедра радиосистем и обработки сигналов Дисциплина «Прикладные пакеты моделирования»
Лабораторная работа №2
Операции с матрицами
Выполнили:
Проверил:Степанов А. Б.
Санкт-Петербург
1.Определение длины вектора и размера матрицы.
>>A = [120 14; 45 1]
A =
120 14
451
>>Z = [ ]; size(Z) ans =
00
>>B = -pi:pi/32:pi
B =
Columns 1 through 7
-3.1416 |
-3.0434 |
-2.9452 |
-2.8471 |
-2.7489 |
-2.6507 |
-2.5525 |
Columns 8 through 14 |
|
|
|
|
|
|
-2.4544 |
-2.3562 |
-2.2580 |
-2.1598 |
-2.0617 |
-1.9635 |
-1.8653 |
Columns 15 through 21 |
|
|
|
|
|
|
-1.7671 |
-1.6690 |
-1.5708 |
-1.4726 |
-1.3744 |
-1.2763 |
-1.1781 |
Columns 22 through 28 |
|
|
|
|
|
|
-1.0799 |
-0.9817 |
-0.8836 |
-0.7854 |
-0.6872 |
-0.5890 |
-0.4909 |
Columns 29 through 35 |
|
|
|
|
|
|
-0.3927 |
-0.2945 |
-0.1963 |
-0.0982 |
0 |
0.0982 |
0.1963 |
Columns 36 through 42 |
|
|
|
|
|
|
0.2945 |
0.3927 |
0.4909 |
0.5890 |
0.6872 |
0.7854 |
0.8836 |
Columns 43 through 49 |
|
|
|
|
|
|
0.9817 |
1.0799 |
1.1781 |
1.2763 |
1.3744 |
1.4726 |
1.5708 |
Columns 50 through 56 |
|
|
|
|
|
|
1.6690 |
1.7671 |
1.8653 |
1.9635 |
2.0617 |
2.1598 |
2.2580 |
Columns 57 through 63 |
|
|
|
|
|
|
2.3562 |
2.4544 |
2.5525 |
2.6507 |
2.7489 |
2.8471 |
2.9452 |
Columns 64 through 65 |
|
|
|
|
|
|
3.0434 |
3.1416 |
|
|
|
|
|
>>size(A) ans =
2 2 >>size(Z) ans =
0 0 >>length(B) ans =
65
.
Пояснение:
•что такое длина вектора и размер матрицы, и как они определяются в
MATLAB
Размер матрицы — число строк и столбцов — определяется с помощью функции: size(x)
Длина вектора — число элементов строки (столбца) — определяется с помощью функции: length(x)
•с какой целью и как вводится пустая матрица и каков ее размер
Матрица нулевой размерности — пустая матрица — обозначается как A=[]
•как вводится регулярная сетка; в каком случае допускается не указывать шаг изменения значения переменной
Вектор, формирующий регулярную сетку, вводят в виде:
<начальное значение>:[<шаг>:]<конечное значение>
Шаг, равный единице, можно не указывать, условным признаком чего служат квадратные скобки.
2.Генерирование типовых матриц.
2
>> C = zeros(3,3) C =
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
>> D = ones(3,3) |
|
|
D = |
|
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
>> D1 = eye(3) |
|
|
D1 = |
|
|
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
>>r = [13;15;17]
r =
13
15
17
>>T = toeplitz(r)
T =
13 |
15 |
17 |
15 |
13 |
15 |
17 |
15 |
13 |
>> E = rand(3,3) |
|
|
E = |
|
|
0.9501 |
0.4860 |
0.4565 |
0.2311 |
0.8913 |
0.0185 |
0.6068 |
0.7621 |
0.8214 |
>> F = randn(3,3) |
|
|
F = |
|
|
-1.6041 |
1.4151 |
0.2193 |
0.2573 |
-0.8051 |
-0.9219 |
-1.0565 |
0.5287 |
-2.1707 |
Пояснение:
•как выполняется генерация указанных матриц в MATLAB
В MATLAB можно генерировать большое разнообразие типовых матриц с помощью встроенных функций, список которых может быть выведен по команде:
helpelmat
•что собой представляют матрицы: нулевая, единицы, единичная и Теплица
▪Нулевая матрица M×N zeros(M,N)
▪Матрица единиц M×N ones(M,N)
▪Единичная матрица порядка N eye(N)
▪Матрица Теплица — квадратная матрица с одинаковыми элементами на диагоналях, равными соответствующим элементам первого столбца r
Toeplit
3.Выделение элементов матрицы.
3
>> F |
|
|
F = |
|
|
-1.6041 |
1.4151 |
0.2193 |
0.2573 |
-0.8051 |
-0.9219 |
-1.0565 |
0.5287 |
-2.1707 |
>> F(3,2) |
|
|
ans = |
|
|
0.5287 |
|
|
>> diag(F) |
|
|
ans = |
|
|
-1.6041 |
|
|
-0.8051 |
|
|
-2.1707 |
|
|
>> F(1,:) |
|
|
ans = |
|
|
-1.6041 |
1.4151 |
0.2193 |
>>F(:,3) ans =
0.2193 -0.9219 -2.1707
>>F(2:3,1:3) ans =
0.2573 -0.8051 -0.9219 -1.0565 0.5287 -2.1707
Пояснение:
•как происходит выделение подматриц
▪выделение подматрицы с указанием граничных индексов:
A(M1:M2,N1:N2)
где:
M1:M2 — номера строк с M1 по M2 включительно; N1:N2 — номера столбцов с N1 по N2 включительно.
▪выделение подматрицы с указанием начальных индексов:
A(M1:end;N1:end)
где: M1:
end — строки с M1 до последней включительно; N1:end — столбцы с N1 до последнего включительно.
4.Преобразование матриц.
>>F
F = |
|
|
|
|
|
-1.6041 |
1.4151 |
0.2193 |
|
|
|
0.2573 |
-0.8051 |
-0.9219 |
|
|
|
-1.0565 |
0.5287 |
-2.1707 |
|
|
|
>> H = [F,C] |
|
|
|
|
|
H = |
|
|
|
|
|
-1.6041 |
1.4151 |
0.2193 |
0 |
0 |
0 |
0.2573 |
-0.8051 |
-0.9219 |
0 |
0 |
0 |
-1.0565 |
0.5287 |
-2.1707 |
0 |
0 |
0 |
>> S = [F;D] |
|
|
|
|
|
S = |
|
|
|
|
|
-1.6041 |
1.4151 |
0.2193 |
|
|
|
0.2573 |
-0.8051 |
-0.9219 |
|
|
|
-1.0565 |
0.5287 |
-2.1707 |
|
|
|
1.0000 |
1.0000 |
1.0000 |
|
|
|
1.0000 |
1.0000 |
1.0000 |
|
|
|
1.0000 |
1.0000 |
1.0000 |
|
|
|
4
>> G = repmat(F,2,2) |
|
|
|
|
|
G = |
|
|
|
|
|
-1.6041 |
1.4151 |
0.2193 |
-1.6041 |
1.4151 |
0.2193 |
0.2573 |
-0.8051 |
-0.9219 |
0.2573 |
-0.8051 |
-0.9219 |
-1.0565 |
0.5287 |
-2.1707 |
-1.0565 |
0.5287 |
-2.1707 |
-1.6041 |
1.4151 |
0.2193 |
-1.6041 |
1.4151 |
0.2193 |
0.2573 |
-0.8051 |
-0.9219 |
0.2573 |
-0.8051 |
-0.9219 |
-1.0565 |
0.5287 |
-2.1707 |
-1.0565 |
0.5287 |
-2.1707 |
Пояснение:
•как выполняются указанные преобразования
▪горизонтальная конкатенация (объединение) подматриц (по столбцам):
A=[A1,A2,A3,...]
где A1,A2,A3,... — объединяемые подматрицы с одинаковым числом строк
▪вертикальная конкатенация подматриц (по строкам):
A=[A1;A2;A3;...]
где A1;A2;A3;... — объединяемые подматрицы с одинаковым числом столбцов
▪копирование квадратных матриц, выполняемое с помощью функции: repmat(A,n)
где:
A — исходная квадратная матрица как элемент новой квадратной матрицы;
n — число копий матрицы A по строкам и столбцам
5.Поэлементные операции с матрицами. Для всех элементов матрицы F (см. п. 2) выполнить операцию возведения в квадрат и умножения на 2.
>>F.^2
ans = |
|
|
2.5731 |
2.0026 |
0.0481 |
0.0662 |
0.6482 |
0.8499 |
1.1161 |
0.2796 |
4.7118 |
>> F.*2 |
|
|
ans = |
|
|
-3.2082 |
2.8303 |
0.4386 |
0.5146 |
-1.6102 |
-1.8438 |
-2.1129 |
1.0575 |
-4.3413 |
Пояснение:
•какие символы арифметических операций использованы
Признаком поэлементных арифметических операций является точка перед символом операции
6.Сложение и вычитание матриц.
>>A = [ 12 13 14; 2 3 17; 2 3 5]
A = |
|
|
12 |
13 |
14 |
2 |
3 |
17 |
2 |
3 |
5 |
>> B = [ 3 6 9; 2 1 4; 9 3 1] |
||
B = |
|
|
3 |
6 |
9 |
2 |
1 |
4 |
9 |
3 |
1 |
>> C1 = A+B |
|
|
C1 = |
|
|
15 |
19 |
23 |
5
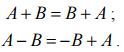
4 |
4 |
21 |
11 |
6 |
6 |
>> C2 = A-B |
|
|
C2 = |
|
|
9 |
7 |
5 |
0 |
2 |
13 |
-7 |
0 |
4 |
Пояснение:
•что собой представляют переменные C1 и С2
сумма и вычитание двух матриц
•является ли операция сложения (вычитания) матриц коммутативной
Для операций сложения и вычитания матриц справедливы обычные законы арифметики:
7.Умножение матриц.
>>C = A*B
C =
188 |
127 |
174 |
165 |
66 |
47 |
57 |
30 |
35 |
Пояснение:
•как должны быть согласованы размеры матриц A и B, чтобы для них была возможна операция умножения
Операция умножения возможна только в том случае, если число столбцов матрицы A равно числу строк матрицы B
•что собой представляет переменная C
Произведением матрицы A размером m n на матрицу B размером n p называется матрица C размером m p, элемент i-й строки и k-го столбца которой равен сумме произведений соответственных элементов i-й строки
матрицы A и k- го столбца матрицы B:
= ∑ ; = 1,2, … , ; = 1,2, … ,
=1
•является ли операция умножения матриц коммутативной
В общем случае умножение матриц не коммутативно:
≠
6
8. Транспонирование и эрмитово сопряжение матриц.
>> F |
|
|
|
F = |
|
|
|
|
-1.6041 |
1.4151 |
0.2193 |
|
0.2573 |
-0.8051 |
-0.9219 |
|
-1.0565 |
0.5287 |
-2.1707 |
>> F' |
|
|
|
ans |
= |
|
|
|
-1.6041 |
0.2573 |
-1.0565 |
|
1.4151 |
-0.8051 |
0.5287 |
|
0.2193 |
-0.9219 |
-2.1707 |
>> P = [1+2i 4-5i 2-4i; 12+2i 13-7i 15-14i; 2+7i 5+6i 7-2i]
P = |
|
|
|
|
|
1.0000 |
+ 2.0000i |
4.0000 |
- 5.0000i |
2.0000 |
- 4.0000i |
12.0000 |
+ 2.0000i |
13.0000 |
- 7.0000i |
15.0000 |
-14.0000i |
2.0000 |
+ 7.0000i |
5.0000 |
+ 6.0000i |
7.0000 |
- 2.0000i |
>> P' |
|
|
|
|
|
ans = |
|
|
|
|
|
1.0000 |
- 2.0000i |
12.0000 |
- 2.0000i |
2.0000 |
- 7.0000i |
4.0000 |
+ 5.0000i |
13.0000 |
+ 7.0000i |
5.0000 |
- 6.0000i |
2.0000 |
+ 4.0000i |
15.0000 |
+14.0000i |
7.0000 |
+ 2.0000i |
>> R = P' |
|
|
|
|
|
R = |
|
|
|
|
|
1.0000 |
- 2.0000i |
12.0000 |
- 2.0000i |
2.0000 |
- 7.0000i |
4.0000 |
+ 5.0000i |
13.0000 |
+ 7.0000i |
5.0000 |
- 6.0000i |
2.0000 |
+ 4.0000i |
15.0000 |
+14.0000i |
7.0000 |
+ 2.0000i |
>> R1 = conj(P) |
|
|
|
|
|
R1 = |
|
|
|
|
|
1.0000 |
- 2.0000i |
4.0000 |
+ 5.0000i |
2.0000 |
+ 4.0000i |
12.0000 |
- 2.0000i |
13.0000 |
+ 7.0000i |
15.0000 |
+14.0000i |
2.0000 |
- 7.0000i |
5.0000 |
- 6.0000i |
7.0000 |
+ 2.0000i |
Пояснение:
•как указанные операции выполняются в MATLAB
▪Транспонирование матрицы — это операция замены каждой строки столбцом с тем же номером.
▪Эрмитово сопряжение матрицы — это операция транспонирования
матрицы с одновременной заменой ее элементов на комплексно сопряженные.
Операции транспонирования и эрмитова сопряжения выполняются с помощью одного и того же символа " ' " (апостроф). Результат зависит от исходной матрицы — является она вещественной или комплексной.
9. Обращение матриц.
>> F |
|
|
F = |
|
|
-1.6041 |
1.4151 |
0.2193 |
0.2573 |
-0.8051 |
-0.9219 |
-1.0565 |
0.5287 |
-2.1707 |
>>det(F) ans =
-1.5732
>>F1 = inv (F)
F1 =
-1.4207 -2.0263 0.7170
|
-0.9741 |
-2.3606 |
0.9041 |
|
0.4542 |
0.4112 |
-0.5894 |
>> |
F2 = F.*F1 |
|
|
F2 |
= |
|
|
7
2.2789 -2.8675 0.1573 -0.2506 1.9005 -0.8335 -0.4798 0.2174 1.2795
Пояснение:
•для какой матрицы возможна операция обращения
Операция обращения возможна только для квадратных матриц с определителем (детерминантом), не равным нулю.
•какая функция служит для вычисления определителя матрицы
Определитель матрицы вычисляется с помощью функции: det(A)
а обратная матрица — с помощью функции: inv(A)
• что собой представляет переменная F2,и с какой целью она вычислена
10.Решить СЛАУ.
>> O = [ 1 2 3; 2 -1 -5; 1 -1 -1]
O =
1 |
2 |
3 |
2 |
-1 |
-5 |
1 |
-1 |
-1 |
>>I = [14; -15; -4]
I =
14 -15 -4
>>X = O\I
X =
1
2
3 >> O*X ans =
14 -15 -4
Пояснение:
•какая операция матричного деления используется и почему
▪Символ левого матричного деления " \" используют при решении систем линейных алгебраических уравнений (СЛАУ):
=
где: A — матрица коэффициентов при неизвестных; B, X — векторыстолбцы свободных членов и неизвестных соответственно.
▪Деление B/A будет ошибочным, т. к. эта операция соответствует−1(B*inv(A)), а умножение матриц в общем случае не коммутативно:
−1 ≠ −1
8
11.Вычисление норм матрицы и вектора.
>> NORMS = [norm(F,1) norm(F) norm(F,inf)]
NORMS = |
|
|
3.3119 |
2.4026 |
3.2385 |
>> X = rand (1,100) |
|
|
X=
Columns 1 through 7
0.9218 |
0.7382 |
0.1763 |
0.4057 |
0.9355 |
0.9169 |
0.4103 |
Columns 8 through 14 |
|
|
|
|
||
0.8936 |
0.0579 |
0.3529 |
0.8132 |
0.0099 |
0.1389 |
0.2028 |
Columns 15 through |
21 |
|
|
|
|
|
0.1987 |
0.6038 |
0.2722 |
0.1988 |
0.0153 |
0.7468 |
0.4451 |
Columns 22 through |
28 |
|
|
|
|
|
0.9318 |
0.4660 |
0.4186 |
0.8462 |
0.5252 |
0.2026 |
0.6721 |
Columns 29 through |
35 |
|
|
|
|
|
0.8381 |
0.0196 |
0.6813 |
0.3795 |
0.8318 |
0.5028 |
0.7095 |
Columns 36 through |
42 |
|
|
|
|
|
0.4289 |
0.3046 |
0.1897 |
0.1934 |
0.6822 |
0.3028 |
0.5417 |
Columns 43 through |
49 |
|
|
|
|
|
0.1509 |
0.6979 |
0.3784 |
0.8600 |
0.8537 |
0.5936 |
0.4966 |
Columns 50 through |
56 |
|
|
|
|
|
0.8998 |
0.8216 |
0.6449 |
0.8180 |
0.6602 |
0.3420 |
0.2897 |
Columns 57 through |
63 |
|
|
|
|
|
0.3412 |
0.5341 |
0.7271 |
0.3093 |
0.8385 |
0.5681 |
0.3704 |
Columns 64 through |
70 |
|
|
|
|
|
0.7027 |
0.5466 |
0.4449 |
0.6946 |
0.6213 |
0.7948 |
0.9568 |
Columns 71 through |
77 |
|
|
|
|
|
0.5226 |
0.8801 |
0.1730 |
0.9797 |
0.2714 |
0.2523 |
0.8757 |
Columns 78 through |
84 |
|
|
|
|
|
0.7373 |
0.1365 |
0.0118 |
0.8939 |
0.1991 |
0.2987 |
0.6614 |
Columns 85 through |
91 |
|
|
|
|
|
0.2844 |
0.4692 |
0.0648 |
0.9883 |
0.5828 |
0.4235 |
0.5155 |
Columns 92 through |
98 |
|
|
|
|
|
0.3340 |
0.4329 |
0.2259 |
0.5798 |
0.7604 |
0.5298 |
0.6405 |
Columns 99 through |
100 |
|
|
|
|
|
0.2091 |
0.3798 |
|
|
|
|
|
>> NORMq = [norm(X,1) norm(X) norm(X,inf)] |
|
|
|
|||
NORMq = |
|
|
|
|
|
|
51.3949 |
5.8054 |
0.9883 |
|
|
|
|
Пояснение:
•смысл указанных норм и способ их вычисления в MATLAB
Норма матрицы (вектора) — это скаляр, с помощью которого оцениваются значения элементов матрицы (вектора).
9
12. Операции с матрицами в задачах математической статистики.
>> max(F) |
|
|
ans = |
|
|
0.2573 |
1.4151 |
0.2193 |
>> min(F) |
|
|
ans = |
|
|
-1.6041 |
-0.8051 |
-2.1707 |
>> sum(F) |
|
|
ans = |
|
|
-1.4033 |
1.1387 |
-2.8733 |
>> prod(F) |
|
|
ans = |
|
|
0.0233 |
-0.6023 |
0.4389 |
>> mean(F) |
|
|
ans = |
|
|
-0.4678 |
0.3796 |
-0.9578 |
>> std(F,1) |
|
|
ans = |
|
|
0.8137 |
0.9125 |
0.9760 |
>> var(F,1) |
|
|
ans = |
|
|
0.6620 |
0.8327 |
0.9527 |
Пояснение:
•какие функции MATLAB использованы в каждом из этих случаев (кроме std и var)
max(F) – Максимальные элементы столбцов min(F) – Минимальные элементы столбцов sum(F) – Сумма элементов столбца
prod(F) – Произведение элементов столбца
mean(F) – Математическое ожидание (среднее значение) элементов столбца
10
