Рис. 10.3. Линейный тренд роста концентрации CO2 в атмосфере

Y B sin		ti		B ,	(10.5)
i 1		T		0
	1

где Yi – рассматриваемая климатическая характеристика; ti – годы, Т1 – период цикла колебаний; B1, B0 – коэффициенты, определяемые

по МНК и связанные с амплитудой гармоники и ее фазой. Статистическая значимость гармонической модели определя-

ется статистической значимостью ее коэффициентов B1 и B0, кото-

рые рассчитываются по формулам:						cp	;
B	i		cp i
1	Y	Y		X X				(10.6)
			i
			X	X
	cp
	B0 Ycp B1X cp				2,			(10.7)

где X i sin ti T1 – функциональное преобразование.

Статистическая значимость коэффициента B1 определяется из следующего неравенства [5]:

B1 B1 Bкр ,

(10.8)

где σB1 – стандартная случайная погрешность коэффициента B1, Bкр

– критическое значение отношения B1/σB1, обычно задается 2.0,

11

что соответствует 95-процентному доверительному интервалу ко- эффициента B1 [13]:

	B1 2 B1 B1 B1 2 B1;
	(10.9)		1 R2
и	B1	Y	X n 1	,
				(10.10)

где Ycp, Xcp, σY, σX – средние значения и стандартные отклонения ря- дов Yi и Xi; R – коэффициент корреляции.

Неравенство (10.9) свидетельствует о том, что выборочные значения коэффициента B1 находятся внутри доверительного ин-

тервала, и если этот коэффициент является статистически значи- мым, то доверительный интервал не должен включать нулевое зна- чение.

Основная проблема при построении гармонической модели – это выбор и задание периода гармоники, что обычно осуществляет- ся на основе анализа автокорреляционной функции:

r f ( ),

где rτ – коэффициенты автокорреляции; τ – лаг, или сдвиг по време-

ни в годах.

(10.11)

Общая формула для вычисления коэффициентов автокорреля-

ции (r) имеет следующий вид:

n

r	n	1			n
	i			Y	Y	Y	Y .
i,i
							(10.12)
	i 1				i		2

Пример построенной автокорреляционной функции показан на

рис. 10.4, из которой следует, что наибольшее значение коэффици- ента автокорреляции rτ = 0,28 имеет место при τ = 25 лет, что соот-

ветствует периоду цикла гармоники Т1 = 25 лет.

Как правило, при моделировании временного ряда стараются учесть не одну гармонику, а сразу несколько, что соответствует ком- позиционной модели вида:

Y B sin			ti		B sin		ti		... B		,
		T					T
i	1					2				0
		1					2		(10.13)

12

Рис. 10.4. Автокорреляционная функция многолетнего ряда среднемесячных температур воздуха января для Санкт-Петербурга

где Yi – рассматриваемая климатическая характеристика; ti – годы, Т1, Т2, … – периоды циклов; B1, B2, …, B0 – коэффициенты, опреде-

ляемые по МНК и связанные с амплитудой гармоник и их фазой. При задании периодов каждой гармоники также может быть

применена автокорреляционная функция с выбором следующих по значимости и величине коэффициентов автокорреляции, например, при τ = 40 на рис. 10.4, что соответствует гармонике с периодом 40 лет и т. д. Вместе с тем необходимо оценивать и статистическую значимость этих коэффициентов автокорреляции и коэффициен- тов Bj в уравнении (10.13).

Еще одним классом модели временного ряда, которая пока еще широко не распространена в климатологии, является модель сту- пенчатых изменений. Эта модель аналогична двум (или несколь- ким) стационарным моделям для двух (или нескольких) частей временного ряда, что характеризуется неизменностью во времени среднего значения и среднего квадратического отклонения для ка-

ждой части ряда: Sr2	t2 const 2, 2	t2 const 2,	(10.14)
	Sr1 t1 const1,	1 t1 const1;

где Sr1, σ1 – среднее значение и среднее квадратическое отклоне-

ния первой части ряда при изменении t1 от 1 до tn; Sr2, σ2 – среднее

13

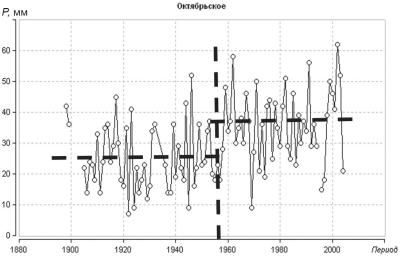
Рис. 10.5. Многолетний ряд сумм осадков января на метеостанции Октябрьская

значение и среднее квадратическое отклонение второй части ряда при изменении t2 от tn + 1 до n; n – объем ряда.

Момент ступенчатых изменений (tn) определяется визуально

или на основе дополнительной информации о факторе и дате нару- шения стационарности (например, изменение индекса атмосфер- ной циркуляции, даты смены регистрирующих приборов), а также может быть определен итерациями при достижении минимально- го значения сумм квадратов отклонений двух частей временного

ряда:

2 n 1 2 n 1 min,

(10.15)

где n1, n2 – объемы каждой1 1из двух 2частей2 временного ряда.

При этом следует задать минимальный объем первой части ряда, например n1 = 10, для которого n2 = n – n1, и затем последо-

вательно увеличивать n1 до m = n – 10, при котором n2 = 10, то есть n1 = 11, 12, ….. m. Иначе эту процедуру можно назвать методом

расширяющегося окна.

Пример модели ступенчатых изменений показан на рис. 10.5 для ряда сумм осадков за январь на метеостанции Октябрьская (За- падная Сибирь), для которого ступенчатые изменения обусловлены сменой регистрирующих приборов.

14

Следующим шагом процесса моделирования временных рядов является оценка эффективности нестационарных моделей по отно- шению к стационарной модели. Наиболее распространенной в ре- грессионном анализе мерой оценки эффективности любой модели является ее остаточная дисперсия, то есть та доля исходной вариа- ции, которую не удалось объяснить с помощью модели, и чем она меньше по величине и больше отличается от исходной вариации, тем модель лучше [5]. Классическая формула для расчета стандарт-

ного отклонения остатков (σε) имеет следующий вид:
	n	i
	1	cp				,
		n 1			2
						(10.16)

где εi – остатки, вычисляемые как разность между фактическими

(Yi) и полученными по модели (Y*i) значениями: εi =Yi – Y*i; εср – среднее значение остатков, которое при их несмещенности (что

получается при расчете по МНК) равно нулю: εср = 0; n – объем

выборки.

Обычно среднее квадратическое отклонение или дисперсия, остатков сравниваются с аналогичными характеристиками выборки и по этому соотношению определяется, какая доля исходного рас- сеяния не объяснена моделью. Наиболее наглядно это выражено в следующем известном соотношении [3, 5, 14, 15]:

где σ	2	, σ	2	– дисперсия остатков и дисперсия выборки (временного
		ε		Y		2	2	или R – коэф-
ряда) соответственно; R – коэффициент1 корреляцииR ,
								2

фициент детерминации для построенной модели.

В соотношении (10.17)(10по.17)полученному коэффициенту корре-

	ляции можно сделать вывод о той части исходного рассеяния, кото-
	2		модели. Так,
	рая не объяснена моделью, то есть о погрешностиY
	если R = 0,8, то правая часть (10.17) будет равна 0,36, то есть
	модель не	2
		19 % и т. д.
	объяснила 36 % исходной вариации, при R = 0,9,
		2Y

Для временного ряда базовой, или исходной, моделью являет- ся модель стационарной выборки, то есть случайных отклонений относительно среднего значения. Тогда стандарт остатков этой мо- дели равен стандартному отклонению временного ряда, то есть σY.

15

Поэтому, когда закономерности во временном ряду полностью от- сутствуют, он представим в виде постоянного среднего, а необъяс- ненная часть исходного рассеяния равна исходной вариации σY.

Для модели линейного тренда и для гармонической модели стандартное отклонение остатков вычисляется по формуле:

y	1 R2 ,	(10.18)
где σy	– стандартное отклонение
исходного ряда (модель стационар-		ного	среднего); σε –
стандартное отклонение остатков относительно			модели линейного
тренда или гармонической модели; R – коэффи-			циент корреляции

уравнения линейного тренда (10.3) или гармони-									ческой модели
(10.5).
				12n 22n2
Для модели ступенчатых
					1	стандарт остатков вычис-
ступ					n n 1				(10.19)
								по формуле:
ляется по информации за два					1	2
или для трех отрезков временного ряда по формуле:
		12n 22n2 23n3
ступ			1
			n1		n2 n3		1	,	(10.20)

где σступ – стандартное отклонение остатков относительно модели ступенчатых изменений; σ1, σ2, σ3 – стандартные отклонения отрез-

ков временного ряда, на которые разбивается ряд наблюдений по дате ступенчатых изменений; n1, n2, n3 – объемы стационарных ча-

стей ряда наблюдений в годах.

Для количественной оценки отличий модели тренда, модели ступенчатых изменений и гармонической модели от модели стацио- нарного среднего рассчитываются относительные погрешности

или отклонения от стационарной модели по формулам:
тр						y y
										100 %,
(10.21)
											(10.22)
гар									гар
						y	y
										100 %,
											(10.23)
ступ									ступ
							y	y
										100 %,

16

где тр, гар, cтуп – относительные погрешности или отличия (в %)

модели тренда, гармонической модели и модели ступенчатых изме- нений от модели стационарной выборки; σεгар – стандартное откло-

нение остатков относительно гармонической модели.

В первом приближении можно принять, что любая модель бу- дет эффективнее модели стационарной выборки, если ≥ 10 %, то есть отличие между моделями гарантированной превышает погреш- ность процесса или погрешность рассматриваемой характеристики. Следующим шагом процедуры построения моделей является оценка статистической значимости нестационарных моделей по от- ношению к стационарной. Полученные относительные отклонения моделей % от стационарной могут и превышать 10 %, однако уста- новить, насколько это отличие является не только достаточным, но и статистически значимым, можно только на основе статистического критерия. Для этой цели достаточно эффективным является извест- ный критерий Фишера для оценки однородности дисперсий. Так, если дисперсии неоднородны, то данная нестационарная модель статистически значимо отличается от модели стационарной выбор-

	2
ки [7, 10]. Статистики критерия Фишера для каждой из трех
Fтр			Y ;	(10.24)
	2
конку- рирующих моделей по отношению к модели стационарной
				выборки
			Y2 ;
вычисляются по формулам:				(10.25)
Fгар	2 гар
Fступ		2Y .		(10.26)
		2ступ

В числителе всегда будет дисперсия исходного ряда наблюде- ний, так как она является наибольшей или, по крайней мере, равна остаточной дисперсии конкурирующей модели. В случае если рас- четное значение статистики Фишера оказывается больше критиче- ского, то дисперсии двух моделей имеют статистически значимое различие, и соответствующая модель (тренда, гармоническая или ступенчатых изменений) статистически эффективнее, чем модель стационарной выборки.

На основе критических значений статистик Фишера можно определить и критическое значение кр %, которое получается при

подстановке, например, (10.24) в (10.21):	17

	кр			1
			1	*		100 %,	(10.27)
				F

где F* – критическое значение статистики критерия Фишера при

уровне значимости α и степенях свободы ν1 и ν2, где ν1 = n1 – 1 и ν2 = n2 – 1, а n1, n2 – объемы выборок.

Принимая, что α = 5 %, а временной ряд один и тот же, то есть n1 = n2 = n и для средней продолжительности ряда, равной n = 61

год, из таблиц критических значений [7] получим F* = 1,53 и из (10.27) кр = 19,4 %. Если же продолжительность ряда равна n = 31

год, то F* = 1,84 и кр = 26,5 %, если n = 120, то F* = 1,35 и кр = 13,8 %

и т.д. Можно также найти, что кр = 10 % соответствует F* =

1,235 и

n примерно равно 500.

Для идентификации климатических изменений во временных рядах часто применяют и стандартную оценку стационарности средних значений и дисперсий за две последовательные части ряда соответственно по критериям Стьюдента и Фишера. Такая оценка по критерию Стьюдента конечно похожа на оценку эффективности модели ступенчатых изменений, но есть и принципиальное отличие, которое связано со способом нахождением момента ступенчатых из- менений или разбиения временного ряда на две части. Если этот год перехода от одного стационарного режима к другому определять по итерационной зависимости (10.15) как и для модели ступенчатых из- менений, то применение критерия Стьюдента будет неправомерно. Это связано с тем, что критические значения статистики любого кри- терия определены при заданной ошибке 1-го рода (уровне значимо- сти α), то есть принятом проценте ошибки в отвержении правильной нулевой гипотезы. И если мы задаем уровень значимости α = 5 %, то это означает, что в пяти случаях из ста мы рискуем допустить ошибку первого рода, то есть отвергнуть правильную гипотезу. По- этому даже для стационарных и случайных выборок в 5 % случаях гарантируется наличие нестационарности, это связано и с наличием альтернативной гипотезы, и с мощностью критерия (рис. 10.6).

При неизвестной дате нарушения стационарности во времен- ном ряду разбиение выборки на части осуществляется случайным образом, то есть обычно пополам. Если же по итерационной зави- симости (10.15) найти разбиение, самое неблагоприятное для усло- вий стационарности, то можно попасть в область ошибки 1-го

Рис. 10.6. Мощность статистического критерия 1-β и уровень значимости α

будет 1 из 100 и т. д. Если же дата нарушения стационарности из- вестна, то следует найти и причину, чтобы обосновать вывод о не- стационарности. Так, если известно, что смена приборов, регистри- рующих осадки, происходила в 1950-х годах, то именно в этот пе- риод и следует ожидать ступенчатый рост средних значений в рядах наблюдений твердых осадков за счет устранения потерь на ветровое выдувание. При этом если гипотеза стационарности отклоняется, то смена приборов оказала влияние

на изменение среднего, а если	гипотеза стационарности не
отклоняется, то изменение среднего	статистически незначимо, но

его все равно необходимо оценить и учесть в виде поправки.

10.2. Статистическая модель внутригодовых изменений

Особенность рядов климатических (климатологических) ха- рактеристик заключается в том, что за каждый год они представ- лены одним значением, то есть для их получения, как правило, необходимо осуществить обобщение информации внутри года [6]. Иногда такое обобщение не требуется и рассматривают выбороч- ные в каждый год величины, например, климатические ряды фор- мируются из максимальных в году срочных температур воздуха или наибольшей в году суммы суточных осадков. Срочная величина мо- жет быть привязана и к дате, например, срочная температура возду- ха на 10 часов утра 9 мая каждого года, для оценки климатических условий проведения парада Победы.

Самым простым способом обобщения внутри года является получение среднегодового значения, например, среднегодовой тем- пературы воздуха, или суммы значений, например, суммы годовых осадков. Также можно сформировать климатические ряды и из дан- ных месячных обобщений, например, среднемесячную температу- ру января. Вместе с тем, большой интерес представляют изменения

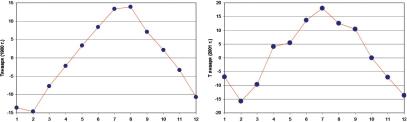
внутри года и представление их для последующих климатических исследований в виде параметров функции годового хода.

Известно, что колебания метеорологических характеристик внутри года представляют собой сложный композиционный про- цесс, так как включают в себя много составляющих разных времен- ных масштабов [11]: мелкомасштабные, мезомасштабные, синоп- тические, продолжительностью от недель до месяцев, сезонные. Очевидно, что количество процессов будет зависеть от периода дискретности или осреднения данных, рассматриваемых внутри года. При дискретности равной сутки будут проявляться процессы, начиная с синоптического масштаба, при дискретности равной ме- сяц – только макросиноптические и внутригодовые изменения, как показано на рис. 10.7.

Таким образом, при моделировании внутригодовых изменений стоят три задачи:

а) разделение сложного процесса на составляющие; б) получение информативных параметров функции внутриго-

довых изменений, которые должны и быть параметрами модели; в) получение информативных показателей для составляющих,

имеющих масштаб меньше годового.

Для температуры воздуха вид внутригодовой функции можно определить, например, аналитически, по формулам приходящей на верхнюю границу атмосферы солнечной радиации, а коэффициен- ты этой гармонической функции найти из данных наблюдений по МНК. Однако, из-за трансформации при прохождении сквозь ат- мосферу и влияния местных условий вид функции искажается и может быть разным для разных метеостанций. Поэтому существует другой подход – определение климатической функции внутригодо- вых колебаний или сезонной функции путем осреднения данных

а)

б)

Рис. 10.7. Примеры внутригодовых изменений среднемесячных температур воздуха на метеостанции Архангельск за 1900 г. (а) и 2001 г. (б)

20