

РГР «Элементы алгебры» Вариант № 1
1. Решить систему методом Крамера
|
|
3 x |
|
2 y |
4 z |
28 |
|
|||
|
|
|
|
|
y |
4 z |
27 |
|
||
|
|
4 x |
|
|||||||
|
|
|
4 x |
|
2 y |
5 z |
34. |
|
||
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||
2. Изобразить корни 2 степени из |
1 |
i |
3 |
на комплексной плоскости. |
||||||
2 |
2 |
|||||||||
|
|
|
|
|
|
|
|
|||
3. Проверить, что векторы |
a 3; |
4; |
2 , b 2; |
1; 2 , c 2; |
4; 5 |
|||||
разложить вектор d (20; 27; 30) |
по этому базису. |
|
|
|||||||
образуют базис и
4. |
Найти |
объем |
пирамиды, |
если |
известны |
координаты |
ее |
вершин |
A 2;1;1 , B 4; 2; 3 , C 3; 4; 2 , D 3; 4; 2 . |
|
|
|
|
||||
5. Даны вершины треугольника
пересечения высоты CH |
и медианы |
A 2;13 ,
BM .
B 8;9 ,
C
2;
7 .
. Найти координаты точки
6. Привести уравнение кривой второго порядка к каноническому виду и построить ее
9x |
2 |
4y |
2 |
36x 8y 4 |
|
|
7. Выполнить действия A (B C) 1 D , где
, |
, |
0 .
, |
. |
8. Решить матричное уравнение
X
A
B
, где 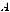

.
9. Исследовав систему на совместность, найти ее общее решение методом Гаусса
x1 2x2 3x3 x4 54x1 8x2 13x3 x4 19x1 2x2 2x3 6x4 10.
10. Найти собственные значения и собственные и присоединенные векторы матрицы линейного оператора и найти вид этой матрицы в базисе из собственных и присоединенных векторов

.

Вариант № 2
1. Решить систему методом Крамера
6 x |
|
2 y |
7 z |
52 |
|
||
|
|
|
y |
4 z 30 |
|
||
4 x |
|
||||||
|
7 x |
|
2 y |
8 z |
58. |
|
|
|
|
||||||
|
|
|
|
|
|
||
2. Изобразить корни 2 степени из i |
на комплексной плоскости. |
||||||
3. Проверить, что векторы a 6; 4; |
|
5 , b 2; |
1; 2 , |
c 5; 4; |
8 |
||
вектор d (44; 30; 54) по этому базису.
образуют базис и разложить
4. |
Найти |
объем |
пирамиды, |
если |
известны |
координаты |
ее |
вершин |
A 2; 4; 2 , B 4; 2; 6 , C 6; 4; 2 , |
D 6; 4; 2 . |
|
|
|
||||
5. Даны вершины треугольника A 2, 16 пересечения высоты CH и медианы BM
, B 10, |
12 , C 2, |
. |
|
4 .
. Найти координаты точки
6. Привести уравнение кривой второго порядка к каноническому виду и построить ее
9x2
7. Выполнить действия |
A (B C) |
1 |
|
|
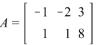 ,
,
4y2 54x 16y 29 0 .
D , где |
|
|
, |
, |
. |
8. Решить матричное уравнение
X
A
B
, где
.
9. Исследовав систему на совместность, найти ее общее решение методом Гаусса
x 2x |
3x |
x |
|
8 |
|||||
|
1 |
2 |
|
3 |
4 |
|
|
||
5x 10x |
16x |
x 39 |
|||||||
|
|||||||||
|
1 |
2 |
|
3 |
|
|
4 |
||
|
x |
2x |
2x |
7x |
|
11. |
|||
|
|
||||||||
1 |
2 |
|
3 |
|
4 |
|
|||
10. Найти собственные значения и собственные и присоединенные векторы матрицы линейного оператора и найти вид этой матрицы в базисе из собственных и присоединенных векторов
.

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант № 3 |
|
|
|
|||||
1. Решить систему методом Крамера |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
5 x |
3 y |
6 z 66 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
6 z 59 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
6 x |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
6 x |
3 y |
|
7 z 75. |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2. Изобразить корни 2 степени из |
|
|
1 |
i |
3 |
на комплексной плоскости. |
|
|
|||||||||||||||
|
2 |
2 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3. Проверить, что векторы a 5; |
6; 4 , b 3; |
1; 3 , c 4; 6; |
7 образуют базис и разложить |
||||||||||||||||||||
вектор d 54; 59; 69 |
по этому базису. |
|
|
|
|
|
|
|
|
||||||||||||||
4. |
|
Найти |
|
объем |
|
пирамиды, |
|
|
|
если |
|
|
известны |
координаты |
ее |
вершин |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
A |
|
3; 2;1 , B |
|
6; 3; 5 |
|
, C |
|
5;6;3 |
|
, D |
|
5; 6; 3 |
|
. |
|
|
|
||||||
5. Даны вершины треугольника A 3, 20 , B 9, |
14 , C 3, |
пересечения высоты CH и медианы BM . |
|
10 .
. Найти координаты точки
6. Привести уравнение кривой второго порядка к каноническому виду и построить ее
9x2 4y2 72x 24y 72 0 .
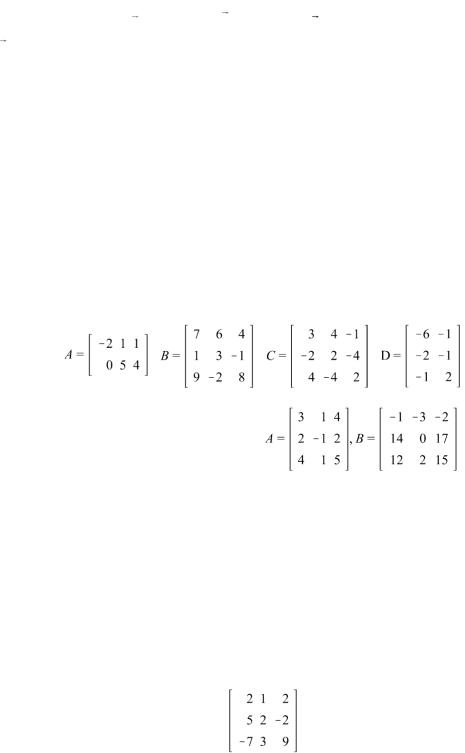
7. Выполнить действия A (B C) 1 D , где |
|
|
|
, |
, |
, |
. |
8. Решить матричное уравнение
X
A
B
, где
.
9. Исследовав систему на совместность, найти ее общее решение методом Гаусса
x1 2x2 3x3 x4 116x1 12x2 19x3 x4 65x1 2x2 2x3 8x4 12.
10. Найти собственные значения и собственные и присоединенные векторы матрицы линейного оператора и найти вид этой матрицы в базисе из собственных и присоединенных векторов
.
Вариант № 4
1. Решить систему методом Крамера
|
3 x |
|
2 y |
4 z |
32 |
|
|
|
|
5 x |
|
y |
5 z 38 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
4 x |
|
2 y |
5 z |
39. |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
2. Изобразить корни 2 степени из |
1 на комплексной плоскости. |
||||||
3. Проверить, что векторы a 3; |
5; 2 , b 2; |
1; 2 , |
c 2; 5; |
5 |
|||
вектор |
d 22; 38; |
35 |
по этому базису. |
образуют базис и разложить
4. |
Найти |
объем |
пирамиды, |
если |
известны |
координаты |
ее |
вершин |
A 3;1; 2 , B 5; 2; 3 , C 3;5; 2 , D 3; 5; 2 . |
|
|
|
|
||||
5. Даны вершины треугольника A 2, 18 , B 14, 12 , C 2, 12 . . Найти координаты точки
пересечения высоты CH |
и медианы BM . |
6. Привести уравнение кривой второго порядка к каноническому виду и построить ее
|
|
16x |
2 |
4y |
2 |
32x 8y 52 |
|
|
|
|
|||
7. |
Выполнить действия A (B C) 1 D , где |
|
||||
|
, |
|
|
|
|
, |
8. |
Решить матричное уравнение |
X A B |
, где |
|||
0 .
, |
. |
.
9. Исследовав систему на совместность, найти ее общее решение методом Гаусса
x |
2x |
|
4x |
x |
3 |
|||
|
1 |
2 |
|
|
3 |
4 |
|
|
3x 6x |
|
13x x |
8 |
|||||
|
|
|||||||
|
1 |
2 |
|
3 |
|
4 |
||
|
x |
2x |
|
3x |
5x |
|
14. |
|
|
|
4 |
||||||
1 |
2 |
|
|
3 |
|
|
||
10. Найти собственные значения и собственные и присоединенные векторы матрицы линейного оператора и найти вид этой матрицы в базисе из собственных и присоединенных векторов
.

Вариант № 5
1. Решить систему методом Крамера
|
6 x |
|
2 |
||||
|
|
5 x |
|
y |
|||
|
|
||||||
|
|
|
|
|
|||
|
|
7 x |
|
2 |
|||
|
|
||||||
|
|
|
|
|
|||
2. Изобразить корни 2 степени из |
|
1 |
i |
3 |
|||
2 |
2 |
||||||
|
|
|
|
||||
3. Проверить, что векторы a 6; |
5; 5 , b |
||||||
вектор d 49; 41; 62 по этому базису. |
|
||||||
y |
7 z |
59 |
|
|
5 z |
41 |
|
y |
8 z |
66. |
|
на комплексной плоскости. |
|||
2; 1; 2 , |
c 5; |
5; 8 образуют базис и разложить |
|
4. |
|
Найти |
|
объем |
|
пирамиды, |
|
если |
|
известны |
координаты |
ее |
вершин |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
A |
|
3; 4; 1 , B |
|
5; 2; 6 |
|
, C |
|
6;5; 2 |
|
, D |
|
6; 5; 2 |
|
. |
|
|
|
5. Даны вершины треугольника A 2, 21 , B 4, |
15 , C 2, |
пересечения высоты CH и медианы BM . |
|
9 .
. Найти координаты точки
6. Привести уравнение кривой второго порядка к каноническому виду и построить ее
16x |
2 |
4y |
2 |
96x 8y 76 |
|
|
7. Выполнить действия A (B C) 1 D , где
, |
, |
0 .
, |
. |
8. Решить матричное уравнение
X
A
B
, где
.
9. Исследовав систему на совместность, найти ее общее решение методом Гаусса
x1 2x2 4x3 x4 115x1 10x2 21x3 x4 54x1 2x2 3x3 7x4 18.
10. Найти собственные значения и собственные и присоединенные векторы матрицы линейного оператора и найти вид этой матрицы в базисе из собственных и присоединенных векторов
.
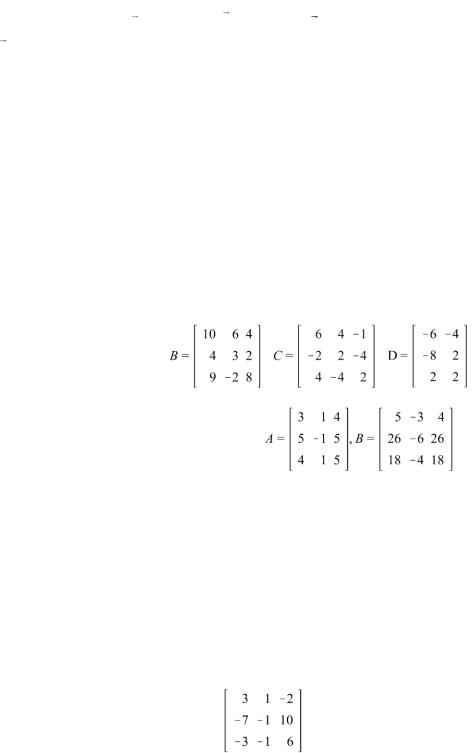
Вариант № 6
1. Решить систему методом Крамера
|
6 x |
3 y |
7 z |
50 |
|
|
|
|
|
y |
2 z 16 |
|
|
|
2 x |
|
||||
|
|
7 x |
3 y |
8 z |
55. |
|
|
|
|
||||
|
|
|
|
|
|
|
2. Изобразить корни 2 степени из |
i |
на комплексной плоскости. |
||||
3. Проверить, что векторы a 6; |
2; 5 , b 3; |
1; 3 , |
c 5; |
2; 8 |
||
вектор d 46; 16; 49 по этому базису. |
|
|
|
|||
образуют базис и разложить
4. |
Найти |
объем |
пирамиды, |
если |
известны |
координаты |
ее |
вершин |
A 1;3; 4 , B 2; 3; 6 , C 6; 2;3 , D 6; 2; 3 . |
|
|
|
|
||||
5. Даны вершины треугольника A 3, 1 , B 21, пересечения высоты CH и медианы BM .
3 , C 3,
11 .
. Найти координаты точки
6. Привести уравнение кривой второго порядка к каноническому виду и построить ее
|
16x |
2 |
|
|
|
||
7. Выполнить действия |
A (B C) |
1 |
|
|
|
||
 ,
,
4y2 128x 16y 176
D , где
,
0 .
, |
. |
8. Решить матричное уравнение
X
A
B
, где
.
9. Исследовав систему на совместность, найти ее общее решение методом Гаусса
x 2x |
4x |
x |
|
15 |
|||||
|
1 |
2 |
|
3 |
4 |
|
|
||
6x 12x |
25x |
x |
89 |
||||||
|
|||||||||
|
1 |
2 |
|
3 |
|
4 |
|
||
|
x |
2x |
3x |
8x |
|
20. |
|||
|
|||||||||
1 |
2 |
|
3 |
|
4 |
|
|
||
10. Найти собственные значения и собственные и присоединенные векторы матрицы линейного оператора и найти вид этой матрицы в базисе из собственных и присоединенных векторов
.

Вариант № 7
1. Решить систему методом Крамера
|
|
|
|
3 x |
|
2 y |
4 z 36 |
|
|
|
||
|
|
|
|
|
|
|
y |
6 z 51 |
|
|
|
|
|
|
|
|
6 x |
|
|
|
|||||
|
|
|
|
|
4 x |
|
2 y |
5 z 44. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
2. Изобразить корни 2 степени из |
1 |
i |
3 |
на комплексной плоскости. |
|
|
||||||
2 |
2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||
3. Проверить, что векторы a 3; |
6; 2 , b 2; |
1; 2 , c 2; 6; |
5 образуют базис и разложить |
|||||||||
вектор d 24; 51; 40 |
по этому базису. |
|
|
|
|
|
||||||
4. |
Найти |
объем |
пирамиды, |
если |
известны |
координаты |
ее |
вершин |
||||
A 4;1;3 , B 6; 2; 3 , C 3;6; 2 , D 3; 6; 2 .
5. Даны вершины треугольника A 2, 23 пересечения высоты CH и медианы BM
, B 20, |
15 , C 2, |
. |
|
17 .
. Найти координаты точки
6. Привести уравнение кривой второго порядка к каноническому виду и построить ее
25x |
2 |
4y |
2 |
50x 16y 91 |
0 |
|
|
||||
7. Выполнить действия A (B C) 1 D , где |
|
||||
, |
|
|
|
, |
|
.
, |
. |
8. Решить матричное уравнение
X
A
B
, где
.
9. Исследовав систему на совместность, найти ее общее решение методом Гаусса
x1 2x2 5x3 x4 43x1 6x2 16x3 x4 11x1 2x2 4x3 5x4 19.
10. Найти собственные значения и собственные и присоединенные векторы матрицы линейного оператора и найти вид этой матрицы в базисе из собственных и присоединенных векторов
.

Вариант № 8
1. Решить систему методом Крамера
|
|
2 x |
3 y |
3 z |
24 |
|
|
|
|
y |
4 z 30 |
|
|
|
|
4 x |
|
|||
|
|
|
3 y |
4 z |
31. |
|
|
|
3 x |
|
|||
|
|
|
|
|
|
|
2. Изобразить корни 3 степени из |
1 |
на комплексной плоскости. |
||||
3. Проверить, что векторы a 2; |
4; 1 , |
b 3; |
1; 3 , |
c 1; |
4; 4 |
|
вектор d 16; 30; 25 по этому базису. |
|
|
|
|
||
образуют базис и разложить
4. |
Найти |
объем |
пирамиды, |
если |
известны |
координаты |
ее |
вершин |
A 1; 1; 2 , |
B 4; 3; 2 , C 2; 4;3 , D 2; 4; 3 . |
|
|
|
||||
5. Даны вершины треугольника A 3, 7 , B 15, 5 , C 3, 3 . . Найти координаты точки
пересечения высоты CH |
и медианы BM . |
6. Привести уравнение кривой второго порядка к каноническому виду и построить ее
25x |
2 |
4y |
2 |
100x 8y 4 |
|
|
7. Выполнить действия A (B C) 1 D , где
, |
, |
0 .
, |
. |
8. Решить матричное уравнение
X
A
B
, где
.
9. Исследовав систему на совместность, найти ее общее решение методом Гаусса
x1 2x2 5x3 x4 94x1 8x2 21x3 x4 35x1 2x2 4x3 6x4 22.
10. Найти собственные значения и собственные и присоединенные векторы матрицы линейного оператора и найти вид этой матрицы в базисе из собственных и присоединенных векторов
.
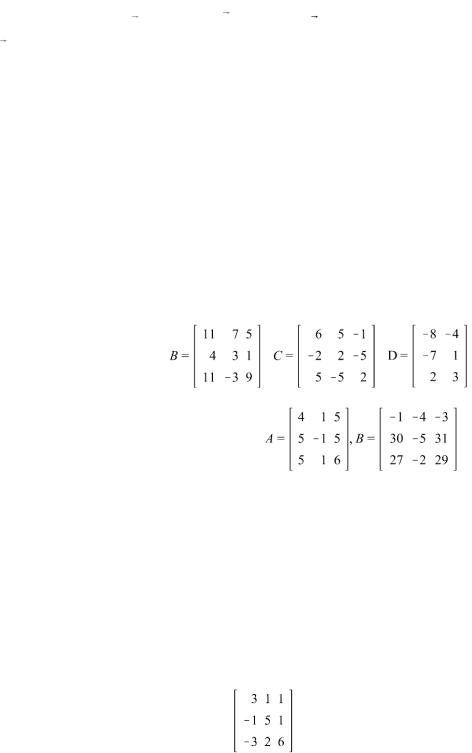
Вариант № 9
1. Решить систему методом Крамера
|
6 x |
3 y |
7 z |
64 |
|
||
|
|
|
y |
4 z 34 |
|
||
|
4 x |
|
|||||
|
|
7 x |
3 y |
8 z |
71. |
|
|
|
|
|
|||||
|
|
|
|
|
|
||
2. Изобразить корни 3 степени из i |
на комплексной плоскости. |
||||||
3. Проверить, что векторы a 6; 4; |
|
5 , b 3; |
1; 3 , |
c 5; |
4; 8 |
||
вектор d 56; 34; 65 |
по этому базису. |
|
|
|
|||
образуют базис и разложить
4. |
Найти |
объем |
пирамиды, |
если |
известны |
координаты |
ее |
вершин |
A 1;3; 2 , B 4; 3; 6 , C 6; 4;3 , D 6; 4; 3 . |
|
|
|
|||||
5. Даны вершины треугольника
пересечения высоты CH |
и медианы |
A 3,
BM
11 , B 9, .
9 , C 3,
1 .
. Найти координаты точки
6. Привести уравнение кривой второго порядка к каноническому виду и построить ее
|
25x |
2 |
||
|
|
|
||
7. Выполнить действия |
A (B C) |
1 |
|
|
|
|
|||
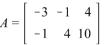 ,
,
4 D ,
y |
2 |
200x 8y 296 |
|
|
где
,
0 .
, |
. |
8. Решить матричное уравнение
X
A
B
, где
.
9. Исследовав систему на совместность, найти ее общее решение методом Гаусса
x1 2x2 5x3 x4 19
6x1 12x2 31x3 x4 113
x1 2x2 4x3 8x4 28.
10. Найти собственные значения и собственные и присоединенные векторы матрицы линейного оператора и найти вид этой матрицы в базисе из собственных и присоединенных векторов
.
