Metod_B1.V.DV.19.02_09.03.01_04.06.2016_laby

4) В криптографии для тестирования качества поточных шифров и исследования генераторов псевдослучайных чисел на их аналитическую сложность.

Отметим следующие результаты исследований ЛС.

Эффективным алгоритмом вычисления ЛС заданной ЛРП и нахождения ЛРС минимальной длины, реализующего эту последовательность и определяющего вид соответствующего характеристического полинома, является алгоритм Берлекэмпа-Месси (АБМ).

Также есть графическая форма отображения ЛС. Функция L(i) с областью значений из множества натуральных чисел называется профилем линейной сложности последовательности

u	[9],	если значение функции L(i) задает линейную сложность подпоследовательности
ui	(s0	, s1 , ... , si 1 ) для всех i 1, lc , где lc – длина последовательности u. Профиль ЛС можно

интерпретировать как двумерный график в декартовых координатах: по оси абсцисс отложены значения длины последовательности ui, а по оси ординат – значения функции L(i). Профиль состоит из множества горизонтальных отрезков, аппроксимируемых прямой L(i)=i/2. Профиль ЛС применяется в качестве статистического теста – для проверки тождественности профилей случайных и псевдослучайных генерируемых последовательностей.

Алгоритм линейного синтеза Берлекампа-Мэсси

Задача алгоритма – найти регистр сдвига с линейной обратной связью, который

соответствующих начальных условиях порождает заданную последовательность

1 , 2 , ...,

и является при этом кратчайшим.

Пусть произвольный РСЛОС задается многочленом обратной связи вида

при

r ,

f (x)	f	n	x	n	f	n 1	x	n 1	... f	1	x 1

и длиной L регистра сдвига. Тогда для построения регистра сдвига надо определить две величины, обозначаемые как пара (L, f(x)), где deg f(x) L.

Рассматриваемая процедура построения является рекурсивной. Для каждого r, начиная с

r = 1, будем строить регистр сдвига, порождающий последовательность		0	,	, ...,	r . Регистр
			1

сдвига минимальной длины, порождающий такую последовательность, обозначим через (Lr, f(r)(x)). Этот регистр не обязательно должен определяться однозначно; возможно существование нескольких таких регистров с одной и той же длиной. К началу r-го шага имеется список регистров сдвига

(L1 , f	(1)	(x)), (L2 , f		(2)	(x)), ... , (Lr 1	, f	(r 1)	(x)) .
Алгоритм			Берлекампа-Мэсси			вычисляет новый кратчайший регистр (Lr, f(r)(x)),

генерирующий последовательность

1, 2 , ..., r . Для этого используется самый последний из

вычисленных регистров, в котором по мере надобности модифицируются длина и коэффициенты в точках съема.

На r-м шаге вычисляется следующий элемент на выходе (r - 1)-го регистра сдвига (над некоторым полем, не обязательно GF(2)):

Lr 1
aˆr f j(r 1)	ar j .
j 1
Пусть r обозначает разность между требуемым элементом на выходе			r	и истинным
элементом, полученным на выходе самого последнего регистра сдвига.
	L
	r 1	ar j
r ar aˆr ar f j
	(r 1)
	j 1
Эквивалентно,

L

r 1

ar j .

r f j

(r 1)

j 0

Если

r

0

то полагаем

(L

,

f

(r)

(x)) (L

r 1

,

f

(r 1)

r

В противном случае изменим коэффициенты многочлена

(x)) и завершаем этим r-тую итерацию.

обратной связи по правилу:

f (r) (x) f (r 1) (x) A xl f (m 1) ,

где А – элемент поля, l – целое число, и f(m-1)(x) – один из многочленов обратной связи,

встречавшийся ранее в сформированном списке регистров сдвига. Используя этот новый многочлен, определим

	L	L	L
'	r 1	r 1	r 1
	(r)	(r 1)	(m 1)	ar j 1 .
r f j		ar j f j	ar j A f j
	j 0	j 0	j 0

Теперь все готово для определения величин m, l и A. Выберем m меньше r и такое, что

m

0; l r

'r r

1	r . Тогда:
m и A m

r m 0 ,

m

так что новый регистр сдвига будет генерировать последовательность

1 , 2 , ..., r . У

нас остался произвол в выборе т, для которого	m 0	. Выбрав в качестве т номер ближайшей
итерации, для которой выполнялось условие

Lm > Lm-1, получим в каждой итерации регистр сдвига минимальной длины.

В более строгой форме алгоритм Берлекампа-Мэсси формулируется следующим образом.

Теорема. Пусть заданы 1 , 2 , ..., n из некоторого поля, и пусть при начальных условиях f(0)(x)=1, t(0)(x)=1 и L0 = 0 выполняются следующие рекуррентные равенства,

используемые для вычисления f(n)(x):

r

Lr

frt

	n 1
f j(r 1) ar j ,
	j 0
		r	(r L			r	1		) (1
(r)	(x)			1
(x)					1						(1
						r				r

	r ) Lr ,
			r	x f			(r 1)		(x)
			) x			(r 1)
		r			t			(x)

,

где r = 1,2,…, 2n; r 1, если одновременно противном случае. Тогда f(2r)(x) является многочленом которого удовлетворяют равенствам f0(2r) = 1 и

	r	0	и	2 L	r	1 r 1,	и	r	0	в

наименьшей степени, коэффициенты

n 1

ar

j 1 r L2r

В этой

f j(2r) ar j

1, ..., 2r .

теореме

r

0,

может обращаться в нуль, но только в том случае, когда r 0 .

Положим тогда по определению

1
	r		r

0

.

Результаты анализа

Для анализа линейной сложности определить линейную сложность и последовательности. Для формирования

будет использоваться программа, позволяющая строящая профиль линейной сложности последовательностей будет использоваться

программная реализация ГПСЧ на основе LFSR, с помощью которой будем получать различные последовательности. Данный программный комплекс моделирует структуру регистра сдвига, на основании которого строится ПСП.

Анализ ПСП, полученных с помощью ГПСЧ на р-ичных регистрах сдвига

1)

p 2;
f (x) x	9	x	4	1.

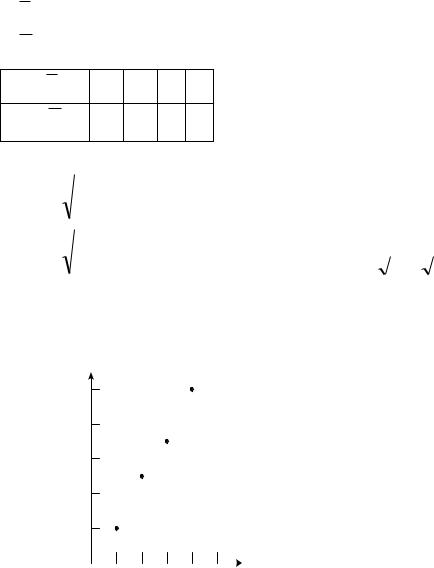
Рис. 2.7. Профиль линейной сложности ПСП при

p 2;	f (x) x	9	x	4	1

На рис. 2.7 представлен

p 2;	f (x) x	9	x	4	1	. Линейная

многочлена n=9.

Порядок выполнения работы

профиль линейной сложности для ПСП при

сложность равна степени характеристического

1.Изучить теоретический материал по данной теме.

2.Используя систему GENERATO.EXE. смоделировать работу генератора ПСЧ, основанного на регистре сдвига. В качестве исходных данных рекомендуется задать структуру ГПСЧ, отобранную по итогам лабораторного занятия №2.

Результат выполнения данного пункта – файл ПСЧ.

3.Используя программный ГПСЧ, созданный на лабораторном занятии №3, создать второй файл ПСЧ.

4.Применяя систему ANALYZE.EXE, проанализировать качество аппаратного и программного генераторов ПСЧ (по двум файлам чисел).

5.Проанализировав результаты исследований, сделать вывод о качестве созданных Вами аппаратного и программного ГПСЧ, отобрать лучший из них для дальнейшего применения в статистическом моделировании.

6.Удалить созданные Вами в процессе работы файлы данных.

7.Результаты исследований по двум файлам оформить в отчет по лабораторной

работе.

Замечание. Формируемые в п.2,3 файлы должны содержать не менее 5000-10000 чисел. Файлы рекомендуется создавать на диске b: и сопровождать расширением *.dat.

Лабораторная работа №8

Автокорреляционная функция

а) Коэффициент корреляции. Пусть выборочные наблюдения состоят из n пар измерений

(x ; y	i
i

будет

); i 1; n [8].

Соответствующей мерой степени линейной зависимости между переменными X и Y

статистика

	1	n
			i		x)			( y	i	y)
	n		(x
r		i 1
							S
				S		x		y

где Sx — стандартное отклонение множества значений х, a Sy - стандартное отклонение значений у.

Статистика r называется коэффициентом произведения моментов линейной корреляции, или просто коэффициентом корреляции [8].

Числитель в формуле для r есть среднее произведение соответствующих отклонений х и у от их выборочных значений (отсюда название произведение моментов). Эту величину называют выборочной ковариацией X и Y и обозначают Sxy. С помощью этого обозначения коэффициент корреляции можно переписать следующим образом:

1

n

n

(xi

) ( yi

)

(xi

)(yi

)

Sxy

x

y

x

y

r

n i 1

i 1

;

Sx Sy

n

n

n

n

(xi

)2

( yi

)2

(xi

)2

( yi

)2

x

y

x

y

i 1

i 1

i 1

i 1

n n

Позже покажем, почему эта статистика будет хорошей мерой линейной корреляции.

Сначала найдем значение r для двух простых случаев.

Пример Наблюдения:

x	2	4	6	8
y	2	5	7	10

График рассеяния показан на рис. 2.12.

Вычисление r:

x 5; y 6.

x x

y y

-3 -1 1 3

-4 -1 1 4

Sx		9 1 1 9	;
	4
		16 1 1 16								26 / 4
Sx	4				;		r										0.997.
										20			32
	( 3)( 4) ( 1)( 1) 1 1 3 4									2	2
Sx							,
			4

Y

10

8

6

4

2

2	4	6	8	10	X

Рис. 2.12. График рассеяния

Любому множеству данных, у которых график рассеяния имеет отчетливое линейное направление, будет соответствовать значение r, близкое по абсолютной величине к 1; оно будет положительным, когда обе переменные одновременно либо возрастают, либо убывают, и

отрицательным, когда одна переменная возрастает, а другая убывает.

б) Свойства коэффициента корреляции.

Из определения коэффициента корреляции r следуют его свойства:

1)r - число, лежащее между –1 и + 1 включительно;

2)если r = + 1 (или –1), то точки выборки лежат на одной прямой;

3)если значение r близко к + 1 (или –1), то существует сильная линейная зависимость между переменными;

4)если r мало (близко к нулю), то корреляция между переменными слабая,

даже в том случае, если график рассеяния указывает на некоторую нелинейную зависимость между переменными;

5) r - безразмерная величина; она не зависит от единиц измерения X и Y и от выбора начала.

Коэффициент корреляции будет хорошей мерой тесноты линейной связи двух переменных.

в) Формула для вычисления.

Как показано в п. а), коэффициент корреляции может быть вычислен непосредственно

по формуле

r		S		xy
	S	x	S		y

. Однако вычисления значительно упростятся, если воспользоваться

следующей формулой для нахождения Sxy:

Sxy xy x y (*). n

Данная формула является эквивалентной формуле

	1	n
Sxy		(xi		) ( yi		).
			x		y
	n i 1

Аналогичные формулы могут быть записаны и для дисперсий:

	2		x2					2
				x						(**);
	Sx		n
	2		y2						2
				y						(***).
	Sy		n

С помощью формул (*), (**), (**) и при необходимости линейного преобразования переменных (r не изменяется при таких преобразованиях) вычисление r становится сравнительно простой процедурой:

xy

Sxy

x y

n

r

Sx Sy

x2

2

y2

2

x

y

n

n

Пример.

Наблюдения:

x	2	4	6	8
y	2	5	7	10

				x 5;
				y 6.
Решение:
x	2			4		16		36		64
y	2			4		25		49		100
x y				4		20		42		80
	x2 120;
	y	2	178;
	x y 146.
	2			120			25		5;
	Sx			4
				178					17
	2						36
	S y			4					2		; r
	Sxy			146			30		13
				4					2			,

		13
				2						0.997.
				17
		5
						2

г) Виды корреляционных функций.

Как было показано в предыдущих пунктах, корреляцию можно вычислить по одной из двух формул:

		n	i			i
								y)
r			(x	x) ( y
	i1
	n		i			n		i
		(x x)			2		( y y)		2
	i1					i1

или

xy

x y

r

n

x2

2

y2

2

x

y

n

n

В зависимости от значения

различают периодическую КФ (ПКФ),

если суммирование идет до	n , где
[6].

верхнего индекса суммирования в данных формулах если суммирование идет до n, и импульсную КФ (ИКФ),

– это относительный сдвиг последовательностей Х и Y

Если Y является задержанной копией Х, то КФ называется автокорреляционной функцией (АКФ), в противном случае – взаимной корреляционной функцией (ВКФ). На рис. 2.13 символически представлена процедура вычисления импульсных АКФ (а), импульсных ВКФ (б), периодических АКФ (в) и периодических ВКФ (г).

X	X	X	X	X	X
X	Y		X		Y
а.	б.		в.		г.

Рис. 2.13 а – ИАКФ; б – ИВКФ; в – ПАКФ; г – ПВКФ

Значение АКФ при 0 называется главным лепестком (ГЛ) АКФ, а при 0 боковым лепестком (БЛ) АКФ [6].

Для анализа последовательностей будет использоваться программная реализация ГПСЧ на основе LFSR, с помощью которой будем получать различные последовательности. Данный программный комплекс моделирует структуру регистра сдвига, на основании которого строится ПСП. Также данная программа позволяет построить периодические автокорреляционные функции.

1)

p 7;
f (x) x	3	x	2	5	x 2.