
Metod_B1.V.DV.23.01_09.03.01_04.06.2016_pz
.PDFФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«КАЗАНСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. А.Н. ТУПОЛЕВА-КАИ»
Чистопольский филиал «Восток» Кафедра компьютерных и телекоммуникационных систем
Методические указания
к практическим занятиям
по учебной дисциплине
«Моделирование»
Индекс по учебному плану: Б1.В.ДВ.23.01
Направление подготовки: 09.03.01 Информатика и вычислительная
техника
Квалификация: Бакалавр
Профиль подготовки: Интегрированные автоматизированные
информационные системы
Вид профессиональной деятельности: научно-исследовательская,
проектно-конструкторская, проектно-технологическая
Рекомендованы УМК ЧФ «Восток» КНИТУ-КАИ
Чистополь
2016 г.
Темы Практикума по дисциплине «Компьютерное моделирование систем»
Учебный материал включает следующие темы по практическим занятиям
Тема 1. Типовые модели систем массового обслуживания
Тема 2. Моделирование непрерывных и дискретных случайных величин Тема 3. Цепи Маркова Тема 4. Вероятностные автоматы
Тема 5. Динамическая категория блоков GPSS
Тема 6. Запоминающая категория блоков GPSS
Тема 7. Моделирование случайных величин на GPSS
Тема 8. Моделирование вычислительной системы средствами языка имитационного моделирования GPSS
Тема 1. Типовые модели систем массового обслуживания
Рассмотрим системы обслуживания, которые могут быть \ проанализированы математическими методами и встречаются во многих прикладных задачах. Системы обслуживания часто коротко описываются фразой «пуассоновский входящий поток, экспоненциальное время обслуживания, один обслуживающий прибор» или символическим представлением М/М/1, введенным Д. Г. Кендэлом. Далее будут объяснены оба эти способа описания.
а) Основные компоненты.
(1) Входящий поток. Требования поступают случайно. Это не значит, что они поступают случайно в обычном смысле этого слова. Правильнее было бы сказать, что они поступают в соответствии с определенным вероятностным законом, который выводится из так называемой вероятностной гипотезы. Это может быть осуществлено следующим образом.
Требования поступают так, что для любых малых интервалов времени (t, t + δ t) верны следующие вероятностные соотношения:
(а) Р [не поступает ни одного требования] =1—λ δ t + о (δt); (б) Р [поступило одно требование] = λ δ t + о (δ t);
(в) Р [поступило два или больше требований] = о (δ t),
где К — константа и символ о (δ t) обозначает величину, которая при δ t, стремящемся к нулю, становится пренебрежимо малой по сравнению с δ t.
Другими словами, безотносительно к тому, в какой момент времени рассматривается система обслуживания, вероятность того, что требования поступят в следующий малый интервал времени б^, равна Яб/ (плюс величины меньшего порядка, чем δ t) и вероятности того, что в этом интервале времени поступят 2, 3 или более требований, являются
бесконечно малыми величинами более высокого порядка, чем δ t. |
|
|
|
||||||||
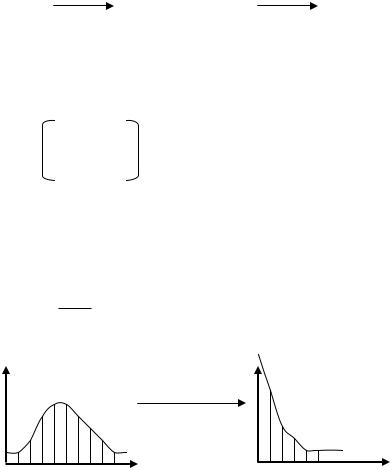
Приняв сформулированную вероятностную гипотезу, можно показать, что число |
|
||||||||||
поступлений требований в произвольный интервал |
л времени длины Т (Т фиксированно) |
||||||||||
подчиняется пуассоновскому закону распределения с параметром λT, т. е. вероятность того, что |
|||||||||||
в течение временного интервала Т поступят п требований, равна |
|
|
|
|
|||||||
P(n)=(λT)ne-λT / n! где n=0,1,2, … |
|
|
|
|
|
|
|||||
Среднее |
число |
требований, |
поступивших |
за |
единицу |
|
времени, |
||||
равно |
Е |
(п) |
IT |
= |
λТ/Т=λ. |
Таким |
образом, |
|
параметр |
λ |
представ |
ляет собой среднюю скорость потока требований, входящего в систему
Из вероятностной гипотезы также следует, что время между последовательными поступлениями требований имеет экспоненциальное распределение с параметром λ, т. е. если переменная t обозначает длину промежутка между последовательными поступлениями требований, то ее функция плотности вероятностей равна λe-λt, t ≥ 0. Легко показать, что средняя длина промежутка между двумя последовательными моментами поступления требований равна λ-1
(2)Механизм обслуживания. Для задания механизма обслуживания вероятностная гипотеза используется следующим образом.
Пусть в момент времени t обслуживается некоторое требование;тогда вероятность, что его обслуживание закончится в интервале
(t, t + δ t), равна μ δ t+ о (δ t), где μ - константа.
Вероятность того,что в течение этого временного интервала обслуживается более чем одно требование, равна о (δ t).
Из этой гипотезы следует, что время обслуживания требований имеет экспоненциальное распределение.
Можно вычислить среднюю скорость обслуживающего потока, которая будет равна μ (рассматриваются только те периоды времени, когда обслуживающий прибор не пуст), и среднее время обслуживания — оно равно 1 / μ .
(3) Дисциплина очереди. Предполагается, что действует правило «первый пришел — первый обслужен». Требования поступают на обслуживающий прибор сразу же, как только он освобождается. На длину очереди ограничений нет.
б) Система обозначений Кендэла. В работе Д. Г. Кендэла, опубликованной в 1953 г.. предложен удобный метод классификации сиестем обслуживания. Он обозначал символом М пуассоновское распределение, полученное из вероятностной гипотезы, и рассмотренная выше модель "получила сокращенное обозначение. М/М/1 ._Буквы указывают типы распределения интервалов между моментами поступлений требований и длительностью обслуживания соответственно; единица указывает на то, что число обслуживающих приборов равно 1. Системы M/G/3 и G/Eк/1 в обозначениях Кендэла расшифровываются так: первая является системой обслуживания с пуассоновским входящим потоком, общей функцией распределения времени обслуживания, тремя приборами, обслуживающими одну очередь; вторая представляет собой систему обслуживания с общим входящим потоком, обслуживающий поток — эрланговый поток порядка k, в системе имеется один обслуживающий прибор.
Эта система обозначений широко применяется в литературе. __
Если п есть число требований в очереди в момент времени t (т. е. число требований, ожидающих обслуживания, плюс число обслуживающихся), то теоретически п может быть любым целым числом от нуля до бесконечности; п — случайная величина. Мы будем обозначать через Рп (t) вероятность того, что в момент времени t в очереди находится п требований. Множество вероятностей {} называется распределением длины очереди в момент t.
г) Стационарное решение для системы обслуживания типа М/М/1.
Если средняя скорость входящего потока λ меньше, чем средняя скорость обслуживания μ, то система обслуживания со временем войдет в стационарный режим. После достаточно большого количества времени, прошедшего от начала процесса, распределение длины очереди станет стационарным, т. е. независимым от t. До тех пор, пока система не войдет в этот режим, она будет находиться в переходном режиме.
Мы обозначим символом Рп стационарную вероятность того, что в очереди находятся п требований. Тогда Рп (t) стремится к Рп при увеличении t при условии, что λ < μ . Множество вероятностей {Р0, P1,...} называется стационарным распределением вероятностей для _ _
длины очереди (сравните со стационарным распределением для состояний регулярной марковской цепи).
Таким образом, уравнения для стационарных вероятно будут следующие:
0 = - λ • Р0 + μ • P1
0 = λ • Рn-1- (λ+ μ) • Pn+ μ• Pn+1n = 1,2,…
первого уравнения мы немедленно получаем
P1= λ • Р0 / μ
Последовательно используя второе уравнение вместе с этим результатом, получаем:
P2= λ • Р1 / μ = ( λ/ μ)2• Р0
P3= λ • Р2 / μ = ( λ/ μ)3• Р0
и т. д.
В общем виде мы имеем
Pn= ( λ/ μ)n• Р0 n=0,1,2,…
(Упражнение. Докажите эту формулу методом индукции)Таким образом, мы получили решение для Рп, причем в формуле присутствует Р0. Воспользовавшись тем, что сумма всех стационарных вероятностей должна равняться единице, можно получить окончательное решение. Поскольку ∑Рп = 1, n=[0,∞) ,
то ∑( λ/ μ)n Р0 = 1, n=[0,∞) , и отсюда
Р0=1/∑( λ/ μ)n = (1 - λ/ μ) , n=[0,∞) , если λ/ μ < 1.
(Сумма бесконечной геометрической прогрессии со знаменателем λ/ μ). Окончательно мы получаем
|
средняя скорость входящего потока |
||
Отношение λ/ μ = |
|
|
от |
|
|
средняя скорость обслуживания |
|
у. |
|
|
|
нагрузкой системы и обозначают греческой буквой ρ. Подставляя ее вместо λ/ μ , получаем
Pn=(1- ρ) ρ n , n=[0,∞)
Как уже упоминалось, зная стационарные вероятности Рп, можно вычислить много интересных характеристик, относящихся к работе системы
обслуживания в стационарном режиме. Далее они приводятся без доказательства в табличной форме.
д) Таблица некоторых характеристик системы обслуживания
ХАРАКТЕРИСТИКА |
ФОРМУЛА |
1. Доля простоев обслуживающего прибора. Фактически это вероятность Ро того, что |
|
обслуживающий прибор свободен |
Po=1- ρ |
2. Средняя длина очереди Е (n) (n—общее число требований в системе) |
E(n)=ρ/(1- ρ) |
3. |
Среднее время ожидания обслуживания для требования Е (ω) (ω —время |
|
ожидания для требования) |
E(ω)=ρ/(1- ρ) μ |
|
4. |
Средняя длина очереди, ожидающей обслуживания |
lср= ρ2/(1- ρ) |
5. |
Среднее время, проведенное требованием в системе |
E=1/(1- ρ) μ |
Проиллюстрируем применение этих формул на трех практических"! примерах.
П р и м е р 1. Требования поступают на обслуживающее устройство супермаркета случайно, причем средний промежуток времени между поступлениями требований равен 0,5 мин. Время обслуживания распределено экспоненциально со средним значением, равным 0,25 мин. Определите (а) среднее число требований в системе обслуживания;, (б) среднее время 'ожидания обслуживания для требования; (в) среднее время, проведенное требованием в системе; (г) долю времени, в течение которого обслуживающий прибор простаивает.
Решение. Средняя скорость входящего потока λ, представляет собой величину, обратную к средней длине промежутка между двумя последовательными поступлениями требований, т. е. к — 1/0,5 = 2 требованиям в минуту. Средняя скорость обслуживания μ равна 1/0,25 = 4 обслуженным требованиям за минуту. Следовательно, нагрузка ρ = λ / μ = 1/2. Поскольку ρ < 1, то через достаточно большое время, прошедшее с начала процесса, система обслуживания войдет в стационарный режим. Конечно, мы предполагаем, что характер поступления требований и их обслуживания остается постоянным.
С помощью формул из таблицы мы находим:
(а) среднее число требований
в очереди
E(n)=ρ/(1- ρ)=1 требование;
(б) среднее время ожидания
обслуживания для требования
E(ω)=ρ/(1- ρ) μ=1/4 мин;
(в) среднее время,
проведенное требованием в системе,
1/(1- ρ) μ=1/2 мин ;
(г) долю простоев
обслуживающего прибора Р0 = 1 — р = 1/2.
П р и м е р 2. Рассмотрим снова обслуживающее устройство супермаркета из примера 1. Предположим, управляющий решил, что он должен будет установить другой обслуживающий прибор, если среднее время ожидания обслуживания превысит 1,5 мин. Как должна измениться средняя скорость входящего потока, чтобы возникла подобная ситуация? Какой тогда будет доля простоев обслуживающего прибора?
Решение. Если Е (w) = 1,5 мин, то с помощью формулы 3 из таблицы
1,5= ρ/(1- ρ) μ= ρ/(1- ρ) 4
так как μ = 4. .
Решая уравнение, получаем ρ = 6/7 = λ/ μ. Следовательно, средняя скорость входящего потока должна быть равна λ = 4 • (6/7)≈3,4 требования в минуту, чтобы среднее время ожидания достигло полутора минут. При этой скорости поступления требований доля времени, которое обслуживающий прибор будет простаивать, равна (1 - р) = 1/7
П р и м е р 3. Человек, ремонтирующий приборы, обнаружил, что они поступают в его мастерскую в соответствии с пуассоновским законом, при этом среднее число поступлений за день равно 3. Затраты времени на ремонт приборы подчиняются экспоненциальному закону со средним временем ремонта, равным 2 ч. Приборы ремонтируются регулярно 8 ч в день.
Вычислите (а) среднее число машин в мастерской, (б) среднее время, проведенное машиной в мастерской перед началом ремонта, (в) среднее время в течение дня, в которое нет машин, ожидающих ремонта.
Решение. Стиральные машины могут рассматриваться как требования, поступающие в ремонтную мастерскую на обслуживание. Средняя скорость входящего потока равна 3 машинам в день (= λ). Обслуживание машин производится со средней скоростью 4 машины в день (= μ). Следовательно, нагрузка системы ρ= 3/4.
Теперь с помощью формул из таблицы №1 получаем требуемые ответы следующим образом:
(а) среднее число машин в мастерской равно
E(n)=ρ/(1- ρ)==(3/4)/(1/4)=3
(б) среднее время, в течение которого машина ожидает обслуживания, равно
E(ω)=ρ/(1- ρ)μ = 3/4
(т. е. 6 ч, так как ночь не принимается в расчет).
(в) в течение доли рабочего времени, равной Р0 = 1 — р = 1/4, нет машин для ремонта; т. е. в среднем человек не работает 2 ч в день.
Упражнение 3.2.8 1. Автомобили прибывают на бензозаправочную станцию, при этом проме-\у жутки
времени между двумя последовательными прибытиями машин имеют экспоненциальное распределение со средним значением, равным 1/2 мин. На обслуживание автомобиля требуется в среднем 1/3 мин, время обслуживания экспоненциально распределено. Определите (а) среднее число автомобилей, ожидающих обслуживания, (б) среднее число автомобилей в очереди (т. е. ожидающие обслуживания плюс те, что обслуживаются), (в) долю времени, в течение которого заправочная станция бездействует.
а) 4/3 б) 2 в)1/3 2. Пациенты входят в кабинет врача в соответствии с пуассоновским законом со
средней скоростью входящего потока, равной 1 человеку в каждые 2 мин. Врач в состоянии уделить каждому из них некоторое время, которое имеет экспоненциальное распределение, со средним временем обслуживания, равным 5/3 мин. Определите (а) среднее число пациентов, ожидающих у кабинета, (б) среднее время, затраченное пациентом как на ожидание, так и на лечение у врача, (в) вероятность; что пациенту совсем не придется ждать, когда он подойдет
а)25/6 б) 25/3 в) 1/6
3. Кассир банка тратит на обслуживание посетителя в среднем 3 мин, и время
обслуживания экспоненциально распределено. |
Клиенты подходят к нему по |
пуассоновскому закону со средней скоростью, |
равной 1 клиенту в 4 мин. |
Найдите (а) вероятность, что по крайней мере один клиент стоит в очереди, (б) вероятность, что в очереди есть более чем два клиента, (в) вероятность, что перед окном кассира вообще нет посетителей, (г) среднее время, проведенное клиентом в банке.
а) ¾ б) 135/64 в)1/4 г)12 мин
4. С какой средней скоростью кассир банка, упомянутый в задании 3, должен обслуживать клиента, чтобы его время ожидания уменьшилось вдвое.
Ответ : 12/5 минут
Тема: Моделирование (получение) случайных величин (дискретных, непрерывных).
zi (0,1) - случайная величина
Тема 2. Моделирование непрерывных и дискретных случайных величин
Алгоритм моделирования дискретной случайной величины.
zi |
|
преобразованиие |
x |
|
|
|
|
x – дискретная случайная величина с заданным законом.
Закон распределения – F(x), должен быть задан по таблице или по формуле.
Табличный способ.
X = x1, x2, … , xn , когда n - конечно p1, p2, … , pn
n
pi 1 - условие стахостичности
n
По формуле (примеры).
p(i, l) cli pi (1 p)l i - биномиальная
F ( x) ( t)i e t - распределение Пуассонаt!
Если р 0, n , то формулу p(i, l) можно аппроксимировать формулой F(x).
|
|
р
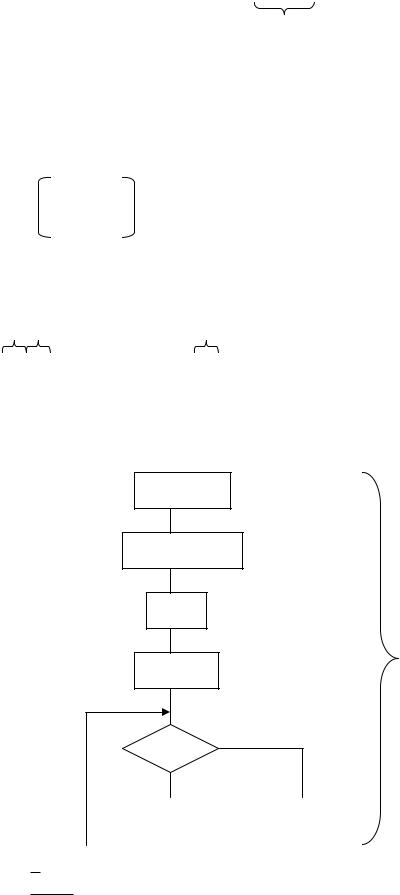
Рассмотрим zi |
0,1) |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
zi = 0, … , 1 |
|
|
0 |
|
|
|
|
|
|
|
1 |
|
||
|
|
|
|
|
|
|
|
|
m разрядов |
|||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
i |
|
|
|
|
|
|||
|
z |
i |
|
; |
i 0,2m 1 |
|||||||
2m 1 |
||||||||||||
|
|
|
|
0,1) |
|
|
|
|
||||
1) Получаем zi |
|
|
|
|
||||||||
2) Преобразование F(z): Q xˆ |
||||||||||||
Q – множество точек |
z |
i |
(2m 1) |
|||||||||
xˆ - множество дискретных случайных величин xi (2m)
x1, x2, … , xn |
0 pi |
1 |
p1, p2, … , pn |
|
|
p1 p2 |
pn |
|
|
|
|
Смотрим в какой интервал попадет zi и по интервалу определяем хi.
1)zi pi , если нет, то 2)
2)zi pi pi 1
zi pi 0
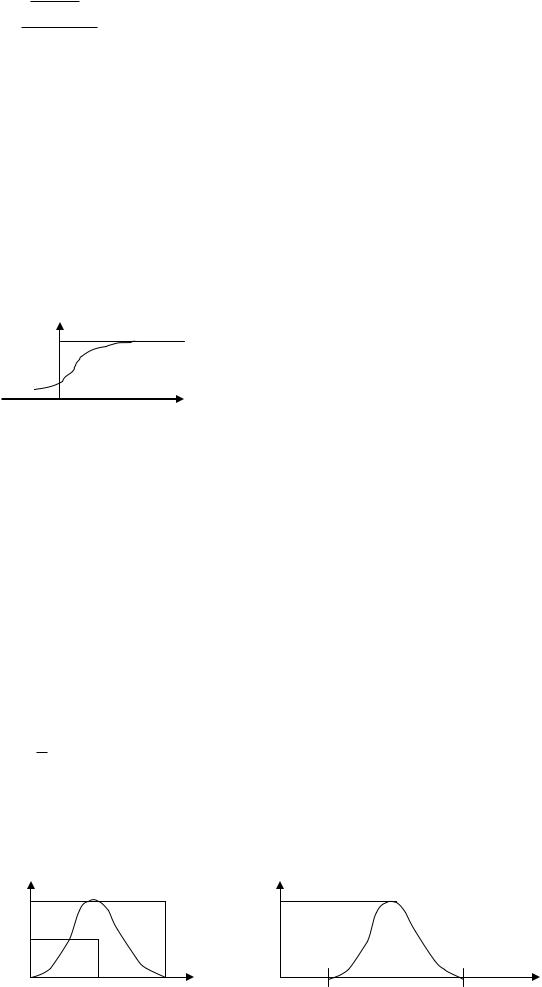
Ввод pi, xi
zi 0,1) , i = 1
:=z
Получение одного значения xi, если надо
:=z - pi N, то ставим счетчик и зацикливаемся.
+
<0
-
|
i++ |
|
Вывод xi |
|
|
|
|
|
|
|
|
|
|
|
n2 - число итераций.
n 210 ,232 - точность представления дискретной случайной величины
N210 ,232 - объем
i210 5,232 5
Алгоритм получения непрерывной случайной величины.
Этот алготитм базируются на нескольких методах моделирования.
Методы:
1.Точные.
2.Стохастические.
3.Приближенные.
4.По специальным формулам.
Получение непрерывной случайной величины.
ЗАКОН ДЛЯ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ:
|
|
|
|
f(x) – функция плотности |
|
1 |
|
x |
распределения |
|
|
|
||
|
|
0 F (x) 1 |
|
|
|
|
|
|
|
- |
0 x1 x2 |
+ x |
|
|
F(x) монотонно возрастает , то есть F(x1)<F(x2) при х1<x2 |
||||
zi |
xi , z i можно поставить в соответствие с F(xi) |
|
||
1) Алгоритм для точного метода.
Дано: F(x)=y
1.zi=xi
2.xi (yi) = F 1 ( yi )
Недостаток: трудно получить обратную функцию F 1 , то есть F (x) F 1 (x)
Пример:
F (x) 1 e x y ln e x ln(1 y)x ln(1 y)
x 1 ln(1 y)
Точный метод основан на методе обратных функций.
2) Метод Неймана (стохастический метод).
Исходно известно f(x), max f(x) = M, x [a,b]
f(x) |
|
f(x) |
M |
|
M |
yi |
(xi,yi) |
|
|
s1 |
s2 |
