КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Предмет и метод аналитической геометрии. Начальные понятия геометрии.

2. Направленные отрезки на оси. Величина направленного отрезка. Линейные операции над направленными отрезками.

1. Декартовы координаты на прямой.

2. Декартовы координаты на плоскости.

3. Расстояние между двумя точками на плоскости.

4. Определение координат точки на плоскости, делящей отрезок в данном отношении.

5. Прямая на плоскости: уравнение с угловым коэффициентом.

6. Прямая на плоскости: уравнение прямой, проходящей через данную точку в данном направлении.

7. Прямая на плоскости: уравнение прямой, проходящей через две данные точки.

8. Прямая на плоскости: уравнение прямой в отрезках.

9. Общее уравнение прямой на плоскости и его исследование.

10. Построение прямой на плоскости по его уравнению.

11. Определение угла между двумя прямыми на плоскости.

12. Условие параллельности прямых на плоскости, заданных уравнениями с угловым коэффициентом.

13. Условие параллельности прямых на плоскости, заданных общими уравнениями.

14. Условие перпендикулярности прямых на плоскости, заданных уравнениями с угловым коэффициентом.

15. Условие перпендикулярности прямых на плоскости, заданных общими уравнениями.

16. Исследование взаимного расположения пар прямых на плоскости, заданных общими уравнениями.

17. Нахождение координат точки пересечения прямых на плоскости.

18. Расстояние от данной точки до данной прямой на плоскости.

19. Линейное уравнение, определение решения линейного уравнения. Равносильность линейных уравнений. Противоречивые и тривиальные уравнения. Общий вид решения уравнения.

20. Системы линейных уравнений: определение решения системы линейных уравнений. Свойства систем уравнений: совместность, несовместность, определенность, неопределенность. Аналогия с исследованием взаимного расположения двух прямых на плоскости.

21. Эквивалентность систем линейных уравнений. Элементарные преобразования систем, приводящие к эквивалентным системам линейных уравнений.

22. Метод Гаусса решения систем линейных уравнений (метод исключения переменных). Основные шаги, прямой и обратный ход метода.

23. Три варианта завершения прямого хода метода Гаусса: а) система несовместная, б) система совместная и неопределенная; в) система совместная и определенная.

24. Общее и частное решение системы линейных уравнений. Привести пример. Фундаментальная система решений.

25. Матрицы, операции над ними и их свойства: сложение матриц, умножение матрицы на число, транспонирование матриц.

26. Произведение матриц: умножение матрицы строки на матрицу-столбец; умножение матрицы на столбец; умножение строки на матрицу; умножение матриц.

27. Условия существования произведения матриц. Свойства операции умножения матриц.

28. Возведение матрицы в степень, условие существования степени матрицы.

29. Понятие определителя матрицы. Формулы для вычисления определителей 2-го и третьего порядков. Свойства определителя.

30. Формулы Крамера для решения систем линейных уравнений. Исследование систем с определителем, равным нулю.

31. Миноры и алгебраические дополнения, их связь с определителем матрицы. Вычисление определителей методом разложения по строке или столбцу.

32. Обратная матрица: определение, условие существования. Присоединенная матрица.

33. Алгоритм вычисления обратной матрицы.

34. Решение систем линейных уравнений с использованием обратной матрицы.

35. Ранг матрицы и его свойства. Алгоритм вычисления ранга матрицы.

36. Исследование систем линейных уравнений с использованием теоремы Кронекера-Капелли.

37. Базисное решение. Однородные и неоднородные системы линейных уравнений.

38. Векторы на плоскости и в пространстве: определение, параллельный перенос, равенство векторов. Классы равных векторов. Коллинеарные и компланарные векторы.

39. Операции над векторами и их свойства.

40. Направляющие косинусы.

41. Координаты вектора. Декартова система координат в пространстве. Радиус-векторы: взаимнооднозначное соответствие между точками и направленными отрезками. Связь координат коллинеарных векторов.

42. Линейно зависимые системы векторов и их свойства.

43. Линейно независимые системы векторов и их свойства.

44. Ранг и базис системы векторов. Разложение вектора по базису.

45. n-мерный вектор и векторное пространство. Размерность и базис векторного пространства.

46. Линейная зависимость и системы линейных уравнений. Связь ранга матрицы с базисом системы векторов.

47. Общее уравнение кривой второго порядка. Определение вида кривой второго порядка по коэффициентам ее уравнения.

48. Определение окружности. Каноническое уравнение окружности. Приведения общего уравнения окружности к каноническому.

49. Определение эллипса. Каноническое уравнение эллипса. Приведение общего уравнения эллипса к каноническому.

50. Координаты фокусов эллипса и его эксцентриситет.

51. Гипербола: определение. Общее и каноническое уравнения гиперболы. Координаты фокусов гиперболы и уравнения его асимптот.

52. Определение параболы. Каноническое уравнение параболы. Приведение общего уравнения параболы к каноническому.

53. Координаты вершины и фокуса параболы. Уравнение директрисы параболы.

54. Скалярное произведение векторов и его свойства.

55. Выражение скалярного произведения в декартовых координатах. Необходимое и достаточное условие ортогональности векторов. Нормальный вектор прямой (на плоскости) и плоскости (в пространстве).

56. Векторное произведение векторов и его свойства.

57. Смешанной произведение векторов и его свойство.

58. Общее уравнение плоскости в пространстве. Уравнение плоскости в отрезках.

59. Условия параллельности и перпендикулярности двух плоскостей в пространстве.

60. Общие уравнения прямой в пространстве. Канонические уравнения прямой в пространстве. Уравнения прямой в пространстве, проходящей через две точки.

61. Условия параллельности и перпендикулярности двух прямых в пространстве.

62. Условия параллельности и перпендикулярности прямой и плоскости в пространстве.

1. Предмет и метод аналитической геометрии. Начальные понятия геометрии.

Предметом аналитической геометрии является исследование форм геометрических образов и их взаиморасположение с помощью алгебры и анализа. Основные методы:

1. Метод координат; 2. Метод линейной геометрии.

Метод координат состоит в том, чтобы определить положение одного геометрического образа относительно другого с помощью чисел. С помощью метода координат каждой линии можно 

поставить в соответствие уравнение  . В аналитической геометрии на плоскости рассматриваются линии, описанные алгебраическими уравнениями 1-го порядка (прямая  ) и алгебраическими уравнениями 2-го порядка (эллипс, окружность, гипербола, парабола  ). С помощью метода координат каждой поверхности в пространстве можно поставить в соответствие уравнение  .

2. Направленные отрезки на оси. Величина направленного отрезка. Линейные операции над направленными отрезками.

Направленные отрезки на оси. Прямую линию с указанным на ней направлением будем называть осью. Отрезок на оси называется направленным, если указано, какая из его граничных точек является началом и какая — концом. Будем обозначать направленный отрезок с началом в точке А и концом в точке В символом . Мы будем рассматривать также и так называемые нулевые направленные отрезки, у которых начало и конец совпадают.

С каждым направленным отрезком сопоставляется его числовая характеристика — так называемая величина направленного отрезка. Величиной АВ направленного отрезка  называется число, равное длине отрезка , взятой со знаком плюс, если направление  совпадает с направлением оси, и со знаком минус, если направление противоположно направлению оси. Величины всех нулевых направленных отрезков считаются равными нулю.

Линейные операции над направленными отрезками. Основное тождество. Предварительно определим равенство направленных отрезков. Направленные отрезки мы будем перемещать вдоль оси, на которой они лежат, сохраняя при этом их длину и направление.

Дваненулевых направленных отрезка называются равными, если при совмещении начал этих отрезков совпадают и их концы. Любые два нулевых направленных отрезка считаютсяравными.

Очевидно, необходимым и достаточным условием равенства двух направленных отрезков на данной оси является равенство величин этих отрезков.

Линейными операциями над направленными отрезками будем называть операции сложения таких отрезков и умножения направленного отрезка на вещественное число.

1. Декартовы координаты на прямой Выберем на прямой определенное направление и некоторую точку О(начало координат). Далее рассмотрим произвольную точку М. Декартова координата точки М - Это величина-О̅М(сверху стрелка) у произвольной точки М есть координата обозначается как М(х)

2. Декартовы координаты на плоскости Две перпендикулярные оси на плоскости с общим началом и одинаковой масштабной единицей образуют прямоугольную систему координат. Одна ось - Ох(абцисс), вторая - Оу(ординат) Через Мх и Му обозначаются проекции произвольной точки М на Ох и Оу

 

3. Расстояние между двумя точками на плоскости  Если на плоскости даны две точки М1(х1; у1) и М2(х2; у2) то расстояние d между ними вычисляется по формуле: d=(x₂-x₂)² +(y₂-y₁)^0.5

4. Определение координат точки на плоскости, делящей отрезок в данном отношении.

Разделить отрезок АВ, в данном отношении λ>0 это значит найти на заданном отрезке такую точку М, для которой имеет место равенство 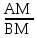= λ

А(x_a, y_a), B(x_b, y_b), M(x_m,y_m)

Формулы для нахождения точек середины:

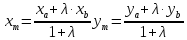
5. Прямая на плоскости: уравнение с угловым коэффициентом.

Уравнение прямой с угловым коэффициентом имеет вид , y = kx + b, где k - угловой коэффициент прямой, b – некоторое действительное число. Уравнением прямой с угловым коэффициентом можно задать любую прямую, не параллельную оси Oy .

6. Прямая на плоскости: уравнение прямой, проходящей через данную точку в данном направлении.

Уравнение прямой, проходящей через данную точку A(x₁, y₁) в данном направлении, определяемом угловым коэффициентом k,

y - y₁ = k(x - x₁). 

Может быть записано уравнение всякой прямой, не параллельной оси Оу. Уравнение прямой, проходящей через данную точку А(х₁, у₁) параллельно оси Оу будет иметь вид

Х₁=Х

7. Прямая на плоскости: уравнение прямой, проходящей через две данные точки. 

Известно, что через две не совпадающие точки можно провести прямую и притом только одну. Найдем уравнение прямой, проходящей через точки P(x1,y1) иQ(x2 ,y2 ) . Используя каноническое уравнение (5.16) и выбирая в

качестве направляющего вектора s векторPQ ={x2 − x1,y2 − y1},

получаем

уравнение вида:

x − x1

=

y − y1

(5.18)

x

− x

y

2

− y

2

1

1

Пример 4. Найти уравнение прямой, проходящей через точкиА(1, 2) и

В(3, 4).

Решение. Применяя формулу (5.18), получаем:

y − 2

= (x −1)

4 − 2

= x

3 −1

y

− 2

−

1

x

− y

+1

= 0