4 курс - Трояновский / ПИУС / ПЦР / Теория_к_Лаб_ПЦР

4.2.1. Эквивалентная весовая функция объекта

с цифровым регулятором в цепи обратной связи

Известно [49], что линейный динамический объект с отрицательной обратной связью также является линейным объектом. Однако в случае применения цифрового регулятора в цепи отрицательной обратной связи возникает дискретный непрерывный канал, что должно очевидно найти отражение при определении эквивалентной весовой функции нового объекта.

Рассмотрим эту проблему более подробно.

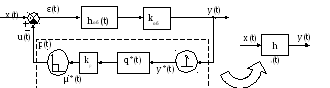
Рис. 4.2. Динамический объект с обратной связью и схема его замещения

И

(4.7)

сходные соотношения (рис. 4.2):

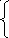
Модель отбора сигнала с периодом отсчета T_s:

Сигнал после цифровой обработки перед восстановлением :

(4.8)

г

(4.10)

де функция обработки q*(θ) может формироваться из исходной непреры вный q(θ) как

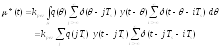
Подставим (2) и (4) в (3):

(4.9)

Функция q(jT_s) - решетчатая цифровая функция (и может быть сформирована и без прототипа q(θ))

(4.11)

Сигнал после восстанавливающего элемента с весовой функцией :

(4.12)

З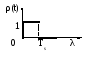аметим, что для ЦАП

На основании (4.11) и (4.12)

(4.13)

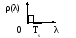
г

(4.14)

де

Н

(4.15)

а основе (4.7), (4.8) и (4.13) получаем:

г

(4.16)

де

И

(4.17)

спользуя , получим для :

Это интегральное уравнение Вольтерра 2-го рода относительно h_э(t).

Заметим, что при численном решении уравнения (4.17) функция h_э(t) заменяется на вектор весовых коэффициентов h_э[0], h_э[1],…, интеграл в правой части (4.17) переходит в сумму и получается система линейных уравнений относительно h_э[i], решение которой позволяет найти весовые коэффициенты эквивалентной весовой функции.

Нетрудно видеть, что выражение (4.17) описывает связь выходного сигнала y(t) со входным x(t) как линейную. Действительно, если сигнал x(t) как представляет собой сумму двух сигналов:

и для каждого из сигналов x₁(t) и x₂(t) существует, в соответствии с (4.17) решения y₁(t) и y₂(t):

то складывая правые и левые части последних выражений, получим, что новый выходной сигнал y(t) в этом случае находится из такого же уравнения, если принять, что

Аналогично доказывается, что изменение выходного сигнала x(t) в произвольное число раз приводит к такому же изменению выходного сигнала y(t).

Таким образом, введение линейного дискретно-непрерывного канала в цепь ОС не нарушает линейности системы, что делает, в частности правомерным переход к эквивалентной схеме (рис. 4.2).

4.2.2. Статический коэффициент усиления эквивалентного звена

Для нахождения весовой функции h_э(t) и коэффициента передачи эквивалентной цепи k_э используем следующий прием. Как известно, весовая функция описывает развитие переходного процесса на выходе системы в ответ на приложение входного сигнала в виде –функции. При этом из (4.17) следует:

(4.18)

где через Н_э(t) обозначена ненормированная весовая функция.

Последнее выражение представляет собой интегральное уравнение Вольтерра 2-го рода относительно h_э(t). Для дискретных моментов времени его решение может быть найдено с применением Z-преобразования или D-преобразования [49, 50]. В этом случае последнее выражение преобразуется к уравнению типа свертки и удается получить замкнутое аналитическое выражение в частотной области для изображения h_э(jT_s), от которого уже можно перейти и к самой функции во временной области. В интересующем нас более общем случае поиска непрерывной весовой функции для решения уравнения (4.18) применяется метод резольвент или метод последовательных приближений [45].

Нетрудно обнаружить признаки того, что получаемые характеристики при двух указанных подходах различаются. На это, в частности, указывает статический коэффициент передачи, который с учетом нормировки весовой функции определяется для линейной системы как

Известно, что для первого подхода (Z-преобразования или D-преобразования) статический коэффициент передачи совпадает с таковым для чисто непрерывной системы и равен

(4.19)

Вместе с этим, интегрирование (4.18) по t дает

(4.20)

откуда следует, что

(4.21)

Сравнение (4.19) и (4.21) показывает, что в общем случае статический коэффициент передачи замкнутой дискретно-непрерывной системы отличается от k_э⁽¹⁾, причем степень отличия зависит от периода отсчетов в системе. Это отличие определяется не только некоторым различием интегральной суммы и интеграла, как это может показаться на первый взгляд, но и деформацией самой функции H_э(t) с изменением периода отсчетов.