
Математика УНК 1 курс экз / Математика готовые шпоры
.docx
|
21. Задача расширения понятия числа. N число, являясь характеристикой класса равносильности конечных множеств, может служить в тоже время и характеристикой увеличения численности множества. Пример: При норме 800 деталей в смену рабочий дал 950 дет, его производительность составила 950-800= 150 дет т.е вместо множества А численностью 800, имеем новое множество B численностью 950 дет т.е переход к более обширному множеству. Число 0 можно рассматривать не только, как пустое множество, но и как характеристику отсутствия изменения, численности множества. На ряду с увеличением численности множества встречаются случаи ее уменьшения. Возникает вопрос: как такое уменьшение охарактеризовать качественно. Пример: Раньше рабочий давал 30 деталей за смену, а сейчас 10 деталей. Здесь произошло уменьшение, а не увеличение т.е кроме термина «изменения» необходимо указать в каком направлении.
|
22. Краткие исторические сведения о возникновении понятия «дробь» и отрицательного числа. О древности понятия "половина" свидетельствует тот факт, что во всех языках оно имеет особое наименование, не происходящее от слова "два". Выражения "большая половина", "меньшая половина" первоначально означало одну из двух частей (не обязательно равных друг другу). Первые представления о целом числе возникли в процессе счёта; первые представления о дробях — из процесса измерения (длин, площадей, веса и так далее). Следы исторической связи исчисления дробей и системы мер можно обнаружить у многих народов. Так, в вавилонской системе мер веса (и денег) 1 талант составлял 60 мин, а одна мина — 60 шекелей. Соответственно с этим в вавилонской математике широко употреблялись шестидесятеричные дроби. В древнеримской весовой (и денежной) системе 1 асс делился на 12 унций; сообразно с этим римляне пользовались двенадцатеричными дробями. Дробь, которую мы называем 1/12, римляне именовали "унцией", хотя бы она употреблялась для измерения длины или иной величины; дробь, которую мы называем 1/8, римляне называли "полторы унции" и тому подобное. Наши "обыкновенные дроби" широко употреблялись древними греками и индийцами. Правила действий с дробями, изложенные индийским учёным Брамагуптой (8 век н. э.), лишь немногим отличаются от наших. Наша запись дробей тоже совпадает с индийской; только дробной черты индийцы не писали; греки записывали сверху знаменатель, а снизу числитель, но чаще пользовались другими записями. Индийское обозначение дробей и правила действий над ними были усвоены в 9 веке в мусульманских странах благодаря узбекскому учёному Мухаммеду Хорезмскому (аль-Хваризми). Они были перенесены в Западную Европу итальянским купцом и учёным Леонардо Фибоначчи из Пизы (13 век). Наряду с "обыкновенными" дробями до 17 века применялись (преимущественно в астрономии) шестидесятеричные дроби. Они были вытеснены десятичными дробями, введёнными голландским купцом и выдающимся инженером-учёным Симоном Стевином (1548—1620). История возникновения отрицательных чисел начинается в VII веке в Китае и Индии. Только тогда они назывались не «отрицательными числами», а были «долгами» или «недостачей». В Европе об отрицательных числах первым написал Леонард Пизанский в своей «Книге абака» в 1202 году. Изначально они также трактовались, как долг. Но даже несмотря на это в XVII такой знаменитый ученый как Паскаль считал, что если из ноля вычесть какое-либо положительное число, то в результате получится ноль. История возникновения отрицательных чисел получила свое развитие с появлением аналитической геометрии. Теперь они наравне с положительными были представлены на геометрической оси. В 1831 году Гаусс полно обосновал, что отрицательные числа абсолютно равнозначны по правам с положительными, а то, что их можно применить не во всех случаях, значения не имеет. История возникновения отрицательных чисел заканчивается в XIX веке, когда Уильям Гамильтон и Герман Грассман создали полную теорию отрицательных чисел. С этого момента начинается история развития данного математического понятия |
23. Множество целых чисел. Свойства множества целых чисел и их геометрическую интерпретацию. Геометрическая интерпретация целых чисел. Каждому целому числу х ставится в соответствие точка М прямой, отстоящая от фиксированной точки 0 на IхIединиц и расположенная на правом луче, если х -положительное число, и на левом, - если х -отрицательное число. Число х, соответствующее точке М, называется координатой этой точки. Тот факт, что точка М имеет координату х, записывается М(х). Изображение целых чисел с помощью точек прямой позволяет задавать не только длины отрезков, но и указывать их направление. Следовательно, геометрически целое число – это направленный отрезок, лежащий на прямой и выходящий из фиксированной точки 0. Геометрически сложение чисел х и у означает перенос точки М(х) на IуIединиц вправо, если у > 0, и влево, если у < 0. Очевидно, что при у > 0 х + у > х, а при у < 0 х + у < х Свойства множеств целых чисел: 1. множество Z чисел, как и множество N чисел можно упорядочить т.е меньшее число предшествует большему. 2. множество Z чисел бесконечно. Множество N чисел – это правильная часть множества Z чисел. Тем не менее, можно установить, взаимно однозначное соответствие, между элементами этих двух множеств:
Т.е множество Z чисел имеет правильную часть (N числа) равносильную всему множеству Z отсюда оно бесконечно. 3. всякое множество равносильное множеству чисел называется счетным. Множество Z чисел – счетно. 4. упорядоченное множество Z чисел дискретно. Определение. Множество называется дискретным, если не у всяких двух его элементов имеется промежуточное.
|
24. Понятие дроби и рационального числа. Дроби:
Каждую из равных частей, на которые
можно разделить элементы будем называть
долей.
Каждый элемент будем называть единицей.
Определение:
дробью или дробным числом называется
пара натуральных чисел a,n,
характеризующихся
мн А одинаковых долей единицы. Первое
из них (а)
показывает, сколько долей содержит
мн А и называется числителем
дроби.
Второе (n)
– на сколько одинаковых долей разделена
единица – это знаменатель. Числитель
и знаменатель называются членами
дроби. Запись дроби:
|
25. Арифметические действия над рациональными числами. Правила при действиях с рациональными числами: • при сложении чисел с одинаковыми знаками необходимо сложить их модули и перед суммой поставить их общий знак; • при сложении двух чисел с разными знаками из числа с большим модулем вычитают число с меньшим модулем и перед полученной разностью ставят знак числа, имеющего больший модуль; • при вычитании одного числа из другого нужно к уменьшаемому прибавить число, противоположное вычитаемому: а - b = а + (-b). • при умножении двух чисел с одинаковыми знаками перемножаются их модули и перед полученным произведением ставится знак плюс; • при умножении двух чисел с разными знаками перемножаются их модули и перед полученным произведением ставится знак минус; • при делении чисел с одинаковыми знаками модуль делимого делят на модуль делителя и перед полученным частным ставится знак плюс; • при делении чисел с разными знаками модуль делимого делят на модуль делителя и перед полученным частным ставится знак минус; • при делении и умножении нуля на любое число, не равное нулю, получается нуль: • на нуль делить нельзя |
26. Свойства множества рациональных чисел (Q) 1. В результате арифметических операций над рациональными числами (сложение, умножение, вычитание, деление, кроме деления на ноль) получается рациональное число. 2. Множество рациональных чисел упорядочено, то есть для любой пары рациональных чисел a и b либо a<b либо a>b. 3. Множество рациональных чисел плотно, то есть для любой пары рациональных чисел a и b существует такое рациональное число c, что a<b<с. Очевидно, что таких чисел бесконечное множество. |
27. Десятичные дроби. Алгоритмы арифметических действий над ними. 1.
Принцип поместного значения цифр
применяется при записи дробей: переход
в значении числа на одно место влево
увеличивает значение цифр в q
раз. Переход на одно место вправо
уменьшает ее значение во столько же
раз; Поставив справа от цифр единиц
знак «дробности» (запятую) понимают
цифру, написанную на 1ом месте справа
от запятой, как обозначение числителя
дроби со знаменателем
Пример:
при q=
3 запись 201,12202 означает число:
2* Определение: десятичной дробью называется любая дробь со знаменателем, представляющим собой степень 10 при условии, что эта дробь записана по принципу поместного значения цифр без знаменателя. По
определению:
Ценная часть десятичной дроби называется характеристикой, дробная часть – мантиссой. 2. Сложение и вычитание десятичных дробей. Эти операции выполняются так же, как и сложение, и вычитание целых чисел. Необходимо только записать соответствующие десятичные знаки один под другим. Умножение десятичных дробей. На первом этапе перемножаем десятичные дроби как целые числа, не принимая во внимание десятичную точку. Затем применяется следующее правило: количество десятичных знаков в произведении равно сумме десятичных знаков во всех сомножителях. Замечание: до простановки десятичной точки в произведении нельзя отбрасывать нули в конце! Деление десятичной дроби на целое число. Если делимое меньше делителя, записываем ноль в целой части частного и ставим после него десятичную точку. Затем, не принимая во внимание десятичную точку делимого, присоединяем к его целой части следующую цифру дробной части и опять сравниваем полученную целую часть делимого с делителем. Если новое число опять меньше делителя, ставим ещё один ноль после десятичной точки в частном и присоединяем к целой части делимого следующую цифру его дробной части. Этот процесс повторяем до тех пор, пока полученное делимое не станет больше делителя. После этого деление выполняется, как для целых чисел. Если делимое больше делителя или равно ему, сначала делим его целую часть, записываем результат деления в частном и ставим десятичную точку. После этого деление продолжается, как в случае целых чисел. Деление одной десятичной дроби на другую. Сначала переносим десятичные точки в делимом и делителе на число десятичных знаков в делителе, то есть делаем делитель целым числом. Теперь выполняем деление, как в предыдущем случае. |
||||||||||||||||
|
28. Рациональные числа как бесконечные десятичные периоды дроби Рассмотрим
целое число 5, обыкновенную дробь |
29. Действительные числа. Понятие иррациональных чисел. Множество действительных чисел - это вместе взятые множества рациональных и иррациональных чисел. Действительное число или как его еще называют вещественное число - это любое положительное число, отрицательное число или нуль. Действительные числа разделяются на рациональные и иррациональные. Вещественные (действительные) числа - это своего рода математическая абстракция, служащая для представления физических величин. Такие числа могут быть интуитивно представлены как отношение двух величин одной размерности, или описывающие положение точек на прямой. Множество вещественных чисел обозначается и часто называется вещественной или числовой прямой. Формально вещественные числа состоят из более простых объектов таких, как целые и рациональные числа. Множество действительных чисел обозначается - R Иррациональные числа – это действительные числа, не являющиеся рациональными и так же - это числа, которые в десятичной записи представляют собой бесконечные непериодические десятичные дроби. Например, бесконечная непериодическая десятичная дробь 4,10110011100011110000… (количество единиц и нулей каждый раз увеличивается на одну) является иррациональным числом. Приведем еще пример иррационального числа: −22,353335333335… (число троек, разделяющих восьмерки, каждый раз увеличивается на две). Иррациональные числа достаточно редко встречаются именно в виде бесконечных непериодических десятичных дробей. Обычно они встречаются в виде корней, степеней, логарифмов и т.п., а также в виде специально введенных букв. Самыми известными примерами иррациональных чисел в такой записи являются арифметический квадратный корень из двух , число «пи» π=3,141592…, число e=2,718281 |
30. Бесконечные десятичные непериодические дроби Это
бесконечные десятичные дроби, не
имеющие периода, т.е. не имеющие группы
повторяющихся цифр после запятой
(пример 41,312509). Рациональное число вида
|
31. Арифметические действия над действительными числами. При сложении действительных чисел с одинаковыми знаками нужно сложить их модули и перед суммой поставить их общий знак. Например, (+3)+(+8)=+11; (-4)+(-9)=-13. При сложении двух действительных чисел с разными знаками модуль суммы равен разности модулей слагаемых. Знак суммы есть знак слагаемого, где модуль больше. Например, (+3)+(-9)=-6; (+11)+(-7)=+4. Вычитание действительных чисел можно заменить сложением: a- b = а + (-b), то есть, чтобы вычесть из числа а число b, достаточно к уменьшаемому прибавить число, противоположное вычитаемому. Например: (+3)-(-8)=(+3)+(+8)=11; (+4)-(+9)=(+4)+(-9)=-5. При умножении (делении) двух действительных чисел нужно умножить (разделить) их модули. Перед результатом нужно поставить знак по правилу знаков из таблицы знаков. Таблица знаков:
Свойства операции умножения действительных чисел: 1.Коммутативный закон сложения: для любой пары чисел а и б: а*б=б*а. 2. Ассоциативный закон умножения: для любой тройки чисел а, б и с: (а*б)*с=а*(б*с).
|
32. Законы сложения и умножения действительных чисел Сложение:
Для любых двух действительных
чисел a и b существует
единственное число c,
называемое суммой этих чисел. a
и
b
– слагаемые, с
– сумма. Свойства операции сложения
действительных чисел: Коммутативный
закон сложения для любой пары чисел a
и
b:
a+b=b+a;
Ассоциативный
закон сложения
для любой тройки чисел a,
b и c:
(a+b)+c=a+(b+c);
Нейтральный
элемент: существует число, обозначаемое
0 и называемое нулем, такое, что для
любого числа а:
a+0=0+a=a;
Для
любого числа a существует
число, обозначаемое (-a),
такое, что
a+(-a)=(-a)+a=0,
число (-a) называется противоположным числу a.
Умножение:
На
множестве действительных чисел
определена операция, называемая
умножением. Для любых двух действительных
чисел a и b
(множителей)
существует
единственное число с,
называемое их произведением. Свойства
операции умножения действительных
чисел: Коммутативный закон умножения
для любой пары чисел a
и
b:
a*b=b*a;
Ассоциативный
закон умножения для любой тройки чисел
a,
b и c:
(a*b)*c=a*(b*с);
Нейтральный
элемент: существует число, обозначаемое
символом 1 и называемое единицей,
такое, что для любого числа а:
а*1=1*а=а;
Для любого числа а,
отличного от 0, существует число,
обозначаемое (1/а),
такое, что a*
|
33. Правило округления чисел и арифметические действия с приближёнными числами. Числа округляют, когда полная точность не нужна или невозможна. Натуральные числа округляют до десятков, сотен, тысяч и т.д. Правила: 1) если первая отброшенная цифра меньше 5, то оставшиеся десятичные знаки сохраняют без изменения; 2) если первая отброшенная цифра больше 5, то к последней оставшейся цифре прибавляют единицу; Пример: Число 25,863 округлённо записывается как – 25,9. В данном случае цифра 8 будет усилена до 9, так как первая отсекаемая цифра 6, больше чем 5. 3) В случае если первая из отсекаемых цифр меньше чем 5, то усиления не производится. Пример: Число 46,48 округлённо записывается как – 46. Число 46 наиболее близко к округляемому числу, чем 47. 4) если первая из отброшенных цифр равна 5 и все отброшенные цифры являются нулями, то последняя оставшаяся цифра оставляется неизменной, если она четная, если не четная то усиливается на единицу. Пример: Число 0,0465 округлённо записывается как – 0,046. В данном случае усиления не делается, так как последняя оставляемая цифра 6 является чётной. Число 0,935 округлённо записывается как – 0,94. Последняя оставляемая цифра 3 усиливается, так как она является нечётной. Арифметические действия с приближёнными числами. При сложении и вычитании приближенных чисел. В окончательном результате следует сохранять столько десятичных знаков, сколько их имеется в слагаемом (или вычитаемом), содержащем наименьшее количество десятичных знаков. Поэтому перед сложением (вычитанием) приближенные числа необходимо округлить, оставив в них на один десятичный знак больше, чем в слагаемом (вычитаемом), имеющем наименьшее количество десятичных знаков. После сложения (вычитания) чисел окончательный результат округляют согласно вышеуказанному правилу. Пример.
Сложить приближенные числа
215,635+1,2+26,18+24,997. Наименьшее количество
десятичных знаков имеет число 1,2.
Поэтому, согласно правилам, следует
складывать числа: 215,64+1,2+26,18+25,00=268,02
Умножение, деление, возведение в степень Точность окончательного результата умножения, деления и возведения в степень приближенных чисел зависит от количества значащих цифр в исходных данных, в связи с чем необходимо соблюдать следующие правила. 1. При умножении и делении приближенных чисел в окончательном результате следует сохранять столько значащих цифр, сколько их имеется в числе (в сомножителе, делимом, делителе) с наименьшим количеством значащих цифр. Поэтому
при умножении или делении чисел с
разным количеством значащих цифр их
округляют, оставляя на одну значащую
цифру больше, чем в числе с наименьшим
количеством значащих цифр. После
выполнения арифметических действий
окончательный результат округляют
согласно правилу. Пример.
Вычислить произведение приближенных
чисел 106,504Х1,ЗХ0,3085. Округлив сомножители,
получим: 107Х 1,3X0,308=42,8428 2.
При возведении приближенного числа
в степень в окончательном результате
следует сохранять столько значащих
цифр, сколько их содержится в основании
данного числа. Примеры: 3.
При извлечении корня в окончательном
результате следует сохранять столько
значащих цифр, сколько их имеется в
подкоренном числе. Примеры:
|
34. Свойства множества действительных чисел Совокупность основных свойств множества действительных чисел может быть принято за систему аксиом, основополагающую для построения теории действительных чисел. 1. Свойства суммы ∀a,b∈R операция a+b называется суммой и обладает следующими свойствами: 1) Коммутативность сложения (∀a,b∈R a+b=b+a) 2) Ассоциативность сложения ∀a,b,c∈R (a+b)+c=a+(b+c) 3) Свойство нуля ∀a∈R ∃!0∈Ra+0=a 4) Свойство противоположного элемента ∀a∈R∃(−a)∈Ra+(−a)=0. 2. Свойства умножения ∀a,b∈R операция a*b называется произведением, и ей присущи следующие свойства:1) Коммутативность умножения ∀a,b∈R a*b=b*a 2) Ассоциативность умножения ∀a,b,c∈R a*(b*c)=(a*b)*c 3) Свойство единицы
∀a∈R
∃1∈Ra⋅1=a.
4) Свойство
обратного числа
∀a∈R
a≠0 ∃ ∀a∈R ∃n∈N a≤n 6. Теорема (аксиома) Дедекинда. Пусть заданы два множества A и B - не пустые, не пересекающиеся и в объединении дающие множество действительных чисел: A≠∅,B≠∅,A∩B=∅,A∪B=R. И пусть ∀a∈A ∀b∈B a<b, тогда существует такое действительное число c, для которого выполняется следующее условие: a≤c≤b. О множествах A и B говорят, что они образуют Дедекиндово сечение, а число c это сечение производит. Это число c принадлежит либо множеству A, тогда в множестве A есть наибольшее число, а в множестве B нет наименьшего числа, либо c принадлежит множеству B, тогда в множестве B оно наименьшее, а в множестве A нет наибольшего. Ясно, что число c, осуществляющее Дедекиндово сечение, единственно. Теорема Дедекинда формулирует свойство полноты (или непрерывности) множества действительных чисел. |

 , где а и n
– N
числа и n>1.
Если 0:n=0,
то это пустое множество долей. Если
a:1=a,
то есть доли элементов представляют
собой сами элементы. Дробь
, где а и n
– N
числа и n>1.
Если 0:n=0,
то это пустое множество долей. Если
a:1=a,
то есть доли элементов представляют
собой сами элементы. Дробь
 , где а-(
, где а-( ,
а n-
,
а n- ,
называется обыкновенной дробью. Если
a<n,
то дробь называется правильной. Если
наоборот, то неправильной. N
число вместе с правильной дробью
называется смешанным числом (3
,
называется обыкновенной дробью. Если
a<n,
то дробь называется правильной. Если
наоборот, то неправильной. N
число вместе с правильной дробью
называется смешанным числом (3 ).
Рациональные
числа:
Отношение
равенства является отношением
эквивалентности на множестве
дробей, поэтому оно порождает на нем
классы эквивалентности. В каждом таком
классе содержатся равные между собой
дроби. Например, множество дробей
).
Рациональные
числа:
Отношение
равенства является отношением
эквивалентности на множестве
дробей, поэтому оно порождает на нем
классы эквивалентности. В каждом таком
классе содержатся равные между собой
дроби. Например, множество дробей
 -
это один класс, множество дробей
-
это один класс, множество дробей
 ...это другой класс и т.д. Дроби одного
класса выражают длину одного и того
же отрезка. Но длина отрезка должна
представляться единственным числом.
Поэтому считают, что равные дроби -
это различные записи одного и того же
положительного рационального числа.
Определение: Положительным
рациональным числом называется класс
равных дробей, а каждая дробь,
принадлежащая этому классу, есть
запись (представление) этого числа.
Например, о
дроби
...это другой класс и т.д. Дроби одного
класса выражают длину одного и того
же отрезка. Но длина отрезка должна
представляться единственным числом.
Поэтому считают, что равные дроби -
это различные записи одного и того же
положительного рационального числа.
Определение: Положительным
рациональным числом называется класс
равных дробей, а каждая дробь,
принадлежащая этому классу, есть
запись (представление) этого числа.
Например, о
дроби
 мы
должны говорить, что она
является записью некоторого
рационального числа. Однако часто для
краткости говорят: - это рациональное
число. Множество всех рациональных
чисел принято обозначать символом Q
мы
должны говорить, что она
является записью некоторого
рационального числа. Однако часто для
краткости говорят: - это рациональное
число. Множество всех рациональных
чисел принято обозначать символом Q ,
на 3-ем
,
на 3-ем
 .
Тогда выражение,
.
Тогда выражение,
 ,
,
 ,….,
,….,

 ,
,
 ,
, ,….,
,…., – это запись суммы
– это запись суммы
 +
+ +
+ +
+ +
+ +…..+
+…..+
 +0*3+1+
+0*3+1+ +
+ +
+ +
+ +
+
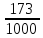 -
обыкновенная дробь; 0,173- десятичная
дробь.
-
обыкновенная дробь; 0,173- десятичная
дробь. и десятичную дробь 8,377. Целое число 5
можно записать в виде бесконечной
десятичной дроби: 5,0000... Десятичную
дробь 8,377 также можно записать в виде
бесконечной десятичной
дроби:
8,377000... Для числа
и десятичную дробь 8,377. Целое число 5
можно записать в виде бесконечной
десятичной дроби: 5,0000... Десятичную
дробь 8,377 также можно записать в виде
бесконечной десятичной
дроби:
8,377000... Для числа
 воспользуемся
методом «деления углом»: начиная со
второй цифры после запятой происходит
повторение одной и той же группы цифр:
18, 18, 18, ... . Таким образом,
воспользуемся
методом «деления углом»: начиная со
второй цифры после запятой происходит
повторение одной и той же группы цифр:
18, 18, 18, ... . Таким образом,
 =
0,3181818... Короче это записывают так:
0,3(18). Повторяющуюся группу цифр после
запятой называют периодом, а саму
десятичную дробь — бесконечной
десятичной периодической дробью. Для
этого надо в периоде записать число
0: 5 = 5,00000... = 5,(0). Так же обстоит дело и
с числом 8,377: 8,377 = 8,377000... = 8,377(0). Чтобы
все было аккуратно, говорят так: 8,377 —
конечная десятичная дробь, а 8,377000... —
бесконечная десятичная дробь. Таким
образом, и число 5, и число
=
0,3181818... Короче это записывают так:
0,3(18). Повторяющуюся группу цифр после
запятой называют периодом, а саму
десятичную дробь — бесконечной
десятичной периодической дробью. Для
этого надо в периоде записать число
0: 5 = 5,00000... = 5,(0). Так же обстоит дело и
с числом 8,377: 8,377 = 8,377000... = 8,377(0). Чтобы
все было аккуратно, говорят так: 8,377 —
конечная десятичная дробь, а 8,377000... —
бесконечная десятичная дробь. Таким
образом, и число 5, и число
 ,
и число 8,377 удалось записать в виде
бесконечной десятичной периодической
дроби. Вообще, любое рациональное
число можно записать в виде бесконечной
десятичной периодической дроби.
,
и число 8,377 удалось записать в виде
бесконечной десятичной периодической
дроби. Вообще, любое рациональное
число можно записать в виде бесконечной
десятичной периодической дроби. нельзя
представить в виде бесконечной
непериодической десятичной дроби.
Такие числа представляются в виде
иррациональных чисел. Поэтому
бесконечные
непериодические дроби не входят в
множество рациональных чисел
нельзя
представить в виде бесконечной
непериодической десятичной дроби.
Такие числа представляются в виде
иррациональных чисел. Поэтому
бесконечные
непериодические дроби не входят в
множество рациональных чисел =
= *a=1,
и
это число называется обратным числу
а.
*a=1,
и
это число называется обратным числу
а. 268,0.
268,0.
 43.
43.
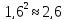 ;
;

 =0,4;
=0,4;
 =0,2
=0,2 ∈
R
∈
R
 =
= a*
a* =1.
Множество R∖{0}R∖{0} относительно
операции умножения является коммутативной
группой. 3.
Дистрибутивность умножения относительно
сложения
∀a,b,c∈R
(a+b)*c=a*c+b*c.
4.
Свойства отношения порядка
Для любых действительных чисел a и b:
или a≤b,
или a≥b.
При этом выполняются следующие
свойства: 1) Свойство
полноты
∀a,b∈R справедливо
одно из трёх утверждений: a=b, a>b(b<a), a<b(b>a).
2) Рефлексивность
∀a∈R
a≤a 3) Свойство
тождества
∀a,b∈R
a≤b и
a≥b⇒a=b
4) Транзитивность
∀a,b,c∈R
a≤b и
b≤c⇒a≤
5) Сохранение
неравенства
∀a,b,c∈R
a≤b⇒a+c≤b+c.
6) Правило
знаков
∀a,b∈Ra≥0
и
b≥0⇒a*b≥0.
5. Аксиома
Архимеда.
=1.
Множество R∖{0}R∖{0} относительно
операции умножения является коммутативной
группой. 3.
Дистрибутивность умножения относительно
сложения
∀a,b,c∈R
(a+b)*c=a*c+b*c.
4.
Свойства отношения порядка
Для любых действительных чисел a и b:
или a≤b,
или a≥b.
При этом выполняются следующие
свойства: 1) Свойство
полноты
∀a,b∈R справедливо
одно из трёх утверждений: a=b, a>b(b<a), a<b(b>a).
2) Рефлексивность
∀a∈R
a≤a 3) Свойство
тождества
∀a,b∈R
a≤b и
a≥b⇒a=b
4) Транзитивность
∀a,b,c∈R
a≤b и
b≤c⇒a≤
5) Сохранение
неравенства
∀a,b,c∈R
a≤b⇒a+c≤b+c.
6) Правило
знаков
∀a,b∈Ra≥0
и
b≥0⇒a*b≥0.
5. Аксиома
Архимеда.