
Аналітична геометрія_2011 Соколовська Г.В., Соколовський С.Ю
..pdfГ.В. СОКОЛОВСЬКА С.Ю. СОКОЛОВСЬКИЙ
АНАЛІТИЧНА ГЕОМЕТРІЯ
Методичні вказівки щодо проведення практичних занять
Одеса-2011
Методичні вказівки розроблено старшими викладачами кафедри «Вища та прикладна математика» Соколовською Галиною Володимирівною та Соколовським Сергієм Юрійовичем.
Методичні вказівки схвалено кафедрою «Вища та прикладна математика» ОНМУ 18 лютого 2011р. (протокол №5).
Рецензенти: доктор фіз.-мат. наук, професор І.Л.Андронов; кандидат фіз.-мат. наук, доцент Ю.О.Григор’єв.
2

Розділ 1. Пряма лінія на площині |
|
||
§1 Різні види рівняння прямої лінії на площині |
|
||
1. Рівняння прямої, що проходить через точку M0 x0 ; y0 |
перпендику- |
||
лярно заданому векторові n A; B (рис. 1) має вигляд |
|
||
A x x0 B y y0 0. |
1 |
||
n |
|
||
l |
M0 |
|
|
Рис. 1 |
|
|
|
|
|
|
|
|
|
|
|
Вектор n називають вектором нормалі прямої |
l . Розкривши дужки в рів- |
нянні 1 отримаємо загальне рівняння прямої |
|
Ax By C 0, |
2 |
вякому Ai B - координати нормального вектора, С Ax0 By0 .
2.Рівняння прямої, що проходить через точку M0 x0 ; y0 паралельно заданому векторові q m;n а) канонічне
x x0 |
|
y y0 |
, |
|
m |
n |
|||
|
|
б) параметричні
x m t x0 ,y n t y0.
Вектор q називають напрямним вектором прямої l (рис. 2).
q
l  M0
M0
Рис. 2
3
4
3
3. Рівняння прямої, що проходить |
через |
дві |
точки |
M0 x0 ; y0 та |
||||
M1 x1 ; y1 (або через точку M0 паралельно векторові M0M1 ) |
||||||||
|
x x0 |
|
y y0 |
. |
|
5 |
||
|
|
|
|
|||||
|
x x |
y y |
|
|
||||
1 |
0 |
|
1 |
0 |
|
x0 ; y0 |
і має заданий |
|
4. Рівняння прямої, що проходить через точку M0 |
||||||||
кутовий коефіцієнт k |
|
|
|
|
|
|
|
|
|
y y0 k x x0 . |
|
6 |
|||||
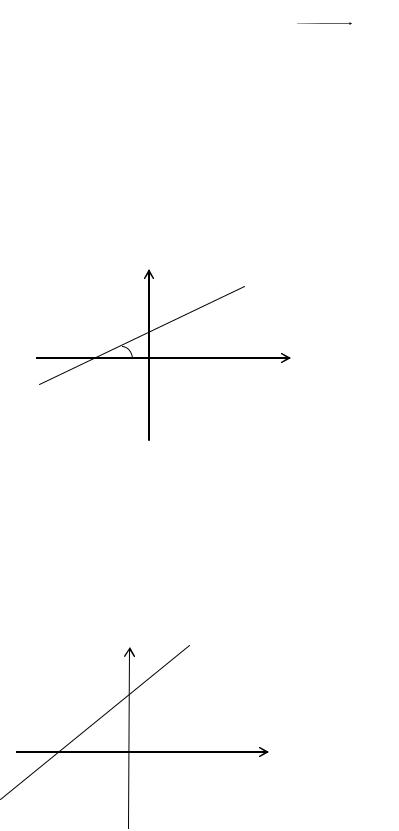
Кутовий коефіцієнт k tg , де - кут між додатним напрямом осі Ox і прямою l (рис. 3).
y
|
|
|
|
M0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
l |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Рис. 3 |
|
|
|
|
|
|
|
|
5. Рівняння прямої, що перетинає осі координат в точках M0 a;0 та |
|||||||||||
M1 0;b ,або відтинає на координатних осях відрізки довжиною |
|
a |
|
та |
|
b |
|
||||
|
|
|
|
||||||||
(рис.4), має вигляд |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
y |
1 . |
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|||
|
a |
|
b |
|
|
|
|
|
|
|
|
y
M1 b
M0 |
a |
|
|
|
0 |
x |
Рис. 4
4

§2 Основні формули
1. Кут між двома прямими. Умови паралельності і перпендикулярності
Один з кутів, що утворюються між двома прямими l1 та l2 дорівнює куту між їх нормальними векторами n1 A1; B1 і n2 A2; B2 , або між їх напрямними векторами q1 m1 ;n1 та q2 m2 ;n2 .
|
|
|
l1 |
l2 |
x |
|
||
|
|
Рис. 5 |
Отже |
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
а) cos |
, l |
|
cos n |
, n |
|
|
||
|
1 |
2 |
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
б) cos |
, l |
|
cos q |
, q |
|
|
||
|
1 |
2 |
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
Умови паралельності прямих
|
n1 n2 |
|
|
|
|
|
A1A2 B1B2 |
|
|
; |
8 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
n1 |
|
n2 |
|
A2 |
B2 |
A2 |
B2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
1 |
1 |
|
2 |
2 |
|
|
|
|
|||||||
|
q1 q2 |
|
|
|
|
m1m2 n1n2 |
|
. |
9 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
q1 |
|
q2 |
|
|
|
|
|
m2 n2 |
m2 |
n2 |
|
|
|
|
||||
|
|
|
|
1 |
1 |
|
2 |
2 |
|
|
|
|
|||||||
а) l || l |
n |
n |
A1 |
|
B1 |
; |
10 |
||||||
|
|
|
|
||||||||||
1 |
2 |
|
1 |
2 |
A2 |
|
B2 |
|
|||||
|
|
|
|
|
|
|
|||||||
б) l |
|| l |
|
q |
q |
m1 |
|
n1 |
. |
11 |
||||
|
|
|
|||||||||||
1 |
2 |
1 |
2 |
|
m2 |
|
|
n2 |
|
||||
|
|
|
|
|
|
|
|
|
|||||
Умови перпендикулярності прямих |
|
|
|
|
|
|
|
|
|
|
|||
а) l1 l2 n1 n2 n1 n2 0 A1A2 B1B2 0; |
12 |
||||||||||||
б) l1 l2 q1 q2 q1 q2 0 m1m2 n1n2 0. |
13 |
||||||||||||
Якщо прямі задано рівняннями з кутовим коефіцієнтами l1 : y k1x b1
і l2 : y k2 x b2 , то кут між ними можна обчислити за формулою
5
tg |
|
|
k2 k1 |
, |
|
|
|
14 |
|||||
|
|
|
|||||||||||
|
|
1 k k |
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
- найменший кут, на який треба повернути проти годинникової стрілки |
|||||||||||||
пряму l1, щоб вона співпала з прямою l2 (рис.5). |
|
||||||||||||
Умови паралельності і перпендикулярності прямих |
|
||||||||||||
а) l1 || l2 k1 k2 ; |
15 |
||||||||||||
б) l1 l2 k1 k2 1. |
16 |
||||||||||||
2. Відстань від точки до прямої |
|
|
|
|
|
|
|
|
|||||
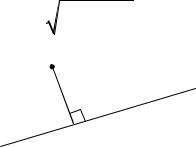
Відстань d від точки M1 x1 ; y1 до прямої l : Ax By C 0 (рис. 6) |
|||||||||||||
можна обчислити за формулою |
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
Ax1 |
By1 |
C |
|
|
. |
17 |
|||||
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
A2 B2 |
|
||||||||
M1 d
l
Рис. 6
Зауважимо, що знак виразу Ax1 By1 C є однаковим для всіх точок, що
лежать в одній півплощині відносно прямої. |
|
||||||||||||||||
3. Поділ відрізка в даному відношенні |
|
||||||||||||||||
Нехай |
точка |
M x; y |
|
ділить |
відрізок M1M 2 (де |
M1 x1; y1 , |
|||||||||||
M2 x2; y2 ) так, що |
M1M |
|
, 0 const . |
|
|||||||||||||
MM2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Координати точки M можна знайти за формулою |
|
||||||||||||||||
|
|
|
x |
x1 x2 |
; y |
y1 y2 |
. |
18 |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
1 |
|
|
|
1 |
|
|||||||
Зокрема, при 1 маємо координати середини відрізка M1M 2 |
|||||||||||||||||
|
|
|
x |
x1 x2 |
; |
y |
y1 y2 |
. |
19 |
||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
||
§3 Приклади і вправи |
|
|
|
|
|
|
|
|
|
|
|
||||||
Вправа |
1.1. |
Записати |
рівняння |
|
прямої, яка проходить |
через точки |
|||||||||||
A 3; 7 та B 6; 2 . |
|
|
|
|
|
|
|
|
|
|
|
||||||
Розв’язання.
6

Скористаємось рівнянням 5 . Одержимо канонічне рівняння прямої
|
|
|
|
|
|
|
|
|
|
|
AB |
: |
x 3 |
|
y 7 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
5 |
|
|
|
|
|
|
або рівносильне йому загальне рівняння AB |
: 5x 3y 36 0. |
|
|
||||||||||||||||||||||
|
Вправа 1.2. Записати рівняння прямої l1 , що проходить через точку |
||||||||||||||||||||||||
M0 x0 ; y0 паралельно до даної прямої. |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Розв’язання. |
|
|
l :3x y 5 0 |
|
||||||||
|
1) |
Нехай |
пряму |
задано |
загальним |
рівнянням |
і |
||||||||||||||||||
M0 5; 1 . Нормальний вектор прямої l |
знаходимо з її загального рівняння |
||||||||||||||||||||||||
n 3;1 . Оскільки пряма l1 |
l , то її нормальний вектор n1 |
n . Не- |
|||||||||||||||||||||||
хай n1 |
n . Тоді, скориставшись рівнянням 1 , одержимо |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
l1 : 3 x 5 1 y 1 0 або l1 : 3x y 14 0 . |
|
|
||||||||||||||||||
|
2) Нехай маємо точку M0 4;0 і пряму, яку задано канонічним рівнянням |
||||||||||||||||||||||||
l : |
|
x 3 |
|
y 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2t 3 |
|
||||||
|
|
|
|
|
|
|
|
або параметричними рівняннями l : |
|
. |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
2 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 5t 1 |
|
|
|||
Пряма |
l1 || l , тоді її напрямний вектор |
q1 |
q . Нехай |
q1 q 2;5 . |
|||||||||||||||||||||
Тоді, скориставшись рівняннями 3 і 4 , одержимо |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
l1 |
|
x 4 |
|
y |
|
|
|
|
x 2t 4 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
: |
|
|
|
|
або l1 |
: |
|
. |
|
|
||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
y 5t |
|
|
|
|
|||
|
3) Нехай маємо точку M0 0;5 і пряму, яку задано рівнянням з кутовим |
||||||||||||||||||||||||
коефіцієнтом l : y 3x 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Оскільки пряма l1 || l , то їх кутові коефіцієнти рівні, тобто k k1 3 . |
||||||||||||||||||||||||
Скориставшись рівнянням 6 , маємо |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
l1 : y 5 3 x 0 або l1 : y 3x 5 . |
|
|
||||||||||||||
|
Вправа 1.3. Записати рівняння прямої l2 , яка проходить через точку |
||||||||||||||||||||||||
M x0 ; y0 перпендикулярно до даної прямої. |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Розв’язання. |
|
|
l |
:x 2 y 5 0 |
|
|||||||
|
1) |
Нехай |
пряму |
задано |
загальним |
рівнянням |
і |
||||||||||||||||||
M 3;2 . Нормальний вектор прямої l |
знаходимо з її загального рівняння |
||||||||||||||||||||||||
7

n 1; 2 . Оскільки пряма l2 l , то її напрямний вектор q2 |
|
n , нехай |
||||||||||||||||||||||||||||||||
q2 n . Тоді, скориставшись рівнянням 3 , одержимо |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
l |
: |
x 3 |
|
y 2 |
або |
l : 2x y 4 0 . |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2) |
Нехай маємо точку M 1;4 і пряму, |
яку задано канонічним рівнян- |
|||||||||||||||||||||||||||||||
ням l : |
x |
|
y 1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q , де q 2; 3 - на- |
||||||||||
|
Оскільки l2 l , то її нормальний вектор n2 |
|
||||||||||||||||||||||||||||||||
прямний вектор прямої l . Візьмемо n2 |
q і, скориставшись рівнянням 1 , |
|||||||||||||||||||||||||||||||||
одержимо l2 :2 x 1 3 y 4 0 або l2 : 2x 3y 14 0 . |
|
|
|
|||||||||||||||||||||||||||||||
|
3) |
Нехай маємо точку M 2;3 і пряму, яку задано рівнянням з кутовим |
||||||||||||||||||||||||||||||||
коефіцієнтом l : y 4x 5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
Оскільки l2 l , |
то |
кутові коефіцієнти цих прямих задовольняють рі- |
|||||||||||||||||||||||||||||||
вність |
|
|
k k2 |
1. |
|
|
Враховуюче |
те, |
|
що |
|
|
k 4, |
отримаємо |
||||||||||||||||||||
4k |
|
1 k |
|
|
1 |
|
. Скориставшись рівнянням 6 |
, маємо |
|
|
|
|||||||||||||||||||||||
2 |
2 |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
l |
: y 3 |
1 |
x 2 або l |
|
: y |
1 |
x |
5 |
. |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
4 |
|
|
|
|
4 |
|
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Вправа 1.4. Знайти координати точки K перетину двох прямих. |
|
|
|||||||||||||||||||||||||||||||
|
1) |
Нехай |
прямі |
задано загальними рівняннями l1 :3x y 5 0 |
і |
|||||||||||||||||||||||||||||
l2 :7x 5y 3 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Розв’язання. |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Прямі перетинаються, тоді і тільки тоді, якщо їх нормальні вектори не є |
|||||||||||||||||||||||||||||||||
паралельними. |
В даному випадку n 3; 1 , n 7;5 |
і |
3 |
1 . Отже, |
||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
7 |
|
5 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
n1 |
n2 . Оскільки точка K перетину прямих належить і прямий l1 |
і прямий |
||||||||||||||||||||||||||||||||
l2 , |
|
то її координати |
задовольняють рівняння |
|
обох |
прямих, |
тобто |
є |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x y 5 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
розв’язком системи рівнянь |
|
Розв’язавши систему, одержимо |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7x 5y 3 |
0. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
x 1 і y 2.
8
Отже, прямі |
l1 і l2 перетинаються в точці K 1; 2 . |
|
|||
2) Пряма l1 :x 2t 1 |
, y 3 t задана параметричними рівняннями, а |
||||
пряма l2 : 3x 4 y 5 0 - загальним. |
|
|
|||
|
|
|
Розв’язання. |
2t 1;3 t |
прямої l1 в |
Підставивши координати поточної точки M |
|||||
загальне рівняння прямої l2 |
, з’ясуємо, при якому значенні параметра t точ- |
||||
ка, що |
належить прямій |
l1 , лежить також |
на прямій |
l2 . Маємо |
|
3 2t 1 4 3 t 5 0 . Звідки t 2. Підставивши значення парамет- |
|||||
ра t в рівняння прямої l1 , одержимо x 5, y 5. |
|
||||
Отже, прямі |
l1 і l2 перетинаються в точці K 5;5 . |
|
|||
Вправа 1.5. Знайти кут між двома прямими. |
|
|
|||
1) |
Нехай |
прямі |
задано |
загальними |
рівняннями |
l1 :3x y 15 0 i l2 :2x y 7 0. |
|
|
|||
Розв’язання.
Запишемо нормальні вектори заданих прямих n1 3; 1 , n2 2;1 .За формулою 8 знайдемо
cos cos l1 |
, l2 |
cos n1 |
, n2 |
|
|
|
n1 |
|
n2 |
|
|
3 |
2 |
|
1 1 |
|
|
1 |
|
. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n1 |
|
n2 |
|
|
|
|
9 1 |
|
4 1 |
2 |
|
|
|||||
Тоді arccos |
|
1 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
2 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
Нехай |
прямі |
задано |
рівняннями з |
кутовими |
|
коефіцієнтами |
|||||||||||||||||||||||
l1 : y 2x 1 i |
l2 : y x 7 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
Розв’язання. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Запишемо кутові коефіцієнти заданих прямих k1 2, k2 |
1. За форму- |
|||||||||||||||||||||||||||||
лою 14 |
маємо |
tg tg l1 , l2 |
|
|
|
|
1 2 |
3. Тоді arctg3. |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
2 1 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Вправа 1.6. |
|
Знайти відстань |
|
від точки |
|
M 5;2 до |
прямої |
|||||||||||||||||||||||
l : 4x 3y 17 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Розв’язання.
9

За формулою 17 |
маємо d |
|
|
4 5 3 2 17 |
|
|
|
|
3 |
0,6 . Отже, відстань |
|||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
42 3 2 |
5 |
|
|||||||||||||||
d від точки M до прямої l дорівнює 0,6. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Вправа 1.7. Знайти площу трикутника, який відтинає від координатного |
|||||||||||||||||||||||||||||||||||||
кута пряма 4x 3y 12 0 . |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Розв’язання. |
|
|
|
|
|
|
|
|
||||||||||||||
Запишемо для заданої прямої рівняння "у відрізках" 7 |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4x 3y 12 |
|
x |
|
y |
1. |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
3 |
4 |
|
|
|
||||||||||||||||||||||||||
Як бачимо, пряма відтинає від другого координатного кута прямокутний |
|||||||||||||||||||||||||||||||||||||
трикутник з катетами |
|
a |
|
|
|
3 |
|
3 та |
|
b |
|
|
|
4 |
|
4 . Його площу обчислимо за |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
формулою S |
1 |
|
a |
|
b |
|
, тоді S |
1 |
3 4 6 кв. од. |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Вправа 1.8. Знайти 1) проекцію точки P 8;12 на пряму, яка проходить через точки A 2; 3 i B 5;1 , 2) точку, симетричну точці P відносно цієї
прямої.
Розв’язання.
1) Запишемо рівняння прямої AB . Скориставшись рівнянням 5 , оде-
ржимо AB : |
x 2 |
|
y 3 |
|
x 2 |
|
y 3 |
або AB :4x 7 y 13 0. |
5 2 |
1 3 |
7 |
|
|||||
|
|
|
4 |
|
||||
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
A |
Q |
|
|
|
||
|
|
|
|
|
M |
|
|
|
Рис. 7
Запишемо тепер рівняння прямої l , що проходить через точку P перпе-
ндикулярно прямій AB . AB 7;4 , AB l . За формулою 1 маємо
l : 7 x 8 4 y 12 0 або l : 7x 4 y 104 0 .
10
