
операційне числення Слинько 2011
.pdfЕлементи операційно числення
Операційне числення відіграє важливу роль при розв’язанні прикладних задач, особливо в сучасній автоматиці і телемеханіці.
Операційне числення – один із методів математичного аналізу, який дозволяє в деяких випадках звести дослідження диференціальних і деяких типів інтегральних операторів до розгляду більш простих алгебраїчних задач.
Методи операційного числення допускають реалізацію наступних умов схеми розв’язку задачі.
1.Від шуканих функцій переходять до деяких інших функцій – їх зображень.
2.Над зображенням проводять операції, відповідні заданим операціям над самими функціями.
3.Отримавши деякий результат при діях над зображеннями, повертаються до самих функцій.
В якості перетворення, яке дозволяє перейти від функції до її зображення, будемо використовувати так зване перетворення Лапласа
(Laplace).
1.Перетворення Лапласа. Оригінали та їх зображення
Головними поняттями операційного числення є поняття функції - оригіналу і функції – зображення.
Нехай f (t) – функція дійсної змінної t виду
f (t) u(t) iv(t),
де u(t) , v(t) – дійсна і уявна частина функції;
i – уявна одиниця, називається комплексною функцією дійсної змінної.
Функція f (t) називається оригіналом, якщо вона задовольняє таким умовам:
1) f (t) визначена і неперервна на осі t , t ( , ) , за винятком
можливо, скінченного числа точок розриву першого роду на кожному інтервалі скінченної довжини;
2) |
f (t) 0 при |
t 0 ; |
|
|
|
|
|
|
|||
3) |
існують такі |
два |
числа M 0 |
і |
S0 0 , |
що |
для |
всіх t 0 , |
|||
|
f (t) |
|
MeS0t , тобто |
при зростанні |
t |
функція |
f (t) |
за |
абсолютною |
||
|
|
||||||||||
величиною може зростати не швидше деякої показникової функції . Число
S0 називається показником зростання функції .
1

Приклади
Показати, що функції є функціями – оригіналами
1) |
e2t sin 3t, ïðè |
t 0, |
|
f (t) |
t 0. |
|
|
|
0, ïðè |
|
|
Розв’язання
Умова (2) виконана в силу завдання функції. Функція f (t) задовольняє умові (1). Накінець, для любих дійсних t
e2t sin 3t e2t ,
Тут в якості М в умові (3) можна взяти число ≥ 1; S0 2.
2) |
e t , лри |
t 0, |
f (t) |
t 0. |
|
|
0 , при |
Розв’язання
Функція f(t) , є неперервною при любих кінцевих t, виконана умова (1), умова (2) виконана в силу завдання функції.
Для любих дійсних t
|
e t |
|
e0 , тут М = 1; S0 |
0 |
|
|
|
||||
t3 |
|
|
|
|
|
|
, при |
t 0, |
|
||
3) f (t) e |
|
||||
|
при |
t 0. |
|
||
0, |
|
||||
Розв’язання
Функція f(t)= et3 не є оригіналом, оскільки не задовольняє умові 3). Зауваження. Для фізичних процесів найменш жорсткою є умова 2),
оскільки звичайно можна вказати початок відліку часу t = 0.
Умови 1) і 3) звичайно звужують клас оригіналів. Так, функції ln1t , tgt
тощо не є оригіналами, оскільки порушується умова 1). Отже до класу функцій – оригіналів входять не всі функції.
Найпростішою функцією – оригіналом є так звана одинична функція
Хевісайда (Heavysiade)
2
1, |
|
при |
t 0, |
|
(t) |
|
|
t 0. |
|
0, |
при |
|||
Очевидно, |
|
|
|
|
(t) (t) |
(t), |
при |
t 0, |
|
|
|
|
t 0, |
|
|
0, |
при |
||
тобто , якщо функція |
(t) |
задовольняє умовам 1) і 3), то (t) (t) |
||
задовольняє усім умовам які накладаються на функції-оригінали .
Приклади для самостійного розв’язування
Перевірити чи є дані функції функціями-оригіналами і знайти показник зростання S0
1) f (t) t 3 ;
2) |
f (t) |
t sin |
1 |
; |
||||
|
t |
|
||||||
|
|
|
|
|
|
|
||
|
1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
3) |
f (t) e t . |
|
|
|
|
|
||
Відповіді:
1)Да, S0 0;
2)Да, S0 0;
3)Ні.
Зображенням |
оригіналу |
|
f (t) |
називається |
функція |
f ( p) |
||||||||||
комплексної змінної |
p i , |
яка визначається інтегралом: |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
( p) e pt f (t) dt. |
|
|
|
|
|
||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
Операцію переходу від оригіналу f (t) до зображення |
|
p називають |
||||||||||||||
f |
||||||||||||||||
перетворенням |
Лапласа . |
Відповідність |
між |
оригіналом |
f (t) і |
|||||||||||
зображенням |
|
p записується у вигляді |
|
|
|
|
|
|
|
|
||||||
f |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (t) f ( p) , або |
|
f ( p) f (t) . |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Теорема (область визначення зображення).
Зображення визначено у тих точках комплексної площини , де
3
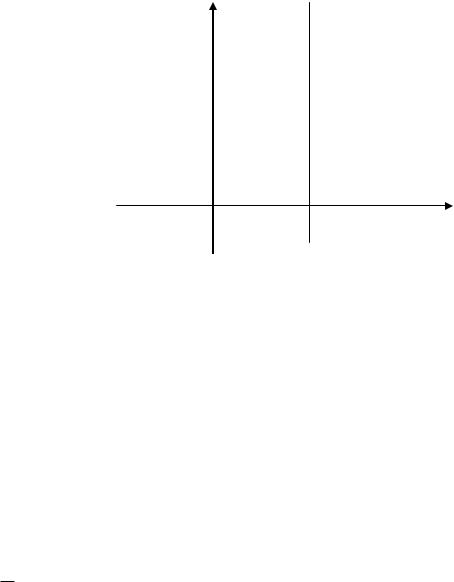
Re p S 0 (дійсна частина комплексного аргументу більша за показник зростання S 0 )
β
Re p S0
0 |
|
S 0 |
|
||
|
|
Рис. 1 |
|
||
|
|
|
|
|
|
Наслідок . Якщо функція |
f ( p) є зображенням функції f (t) , то |
||||
|
|
|
|||
|
lim |
f |
( p) 0 |
|
|
|
p |
|
|||
(необхідна умова існування зображення).
Теорема (Єдність зображення оригіналу)
Будь-якому оригіналу відповідає єдине зображення. Справедливе і обернене твердження: якщо у півплощині, де
Re p S0 ,
f ( p) є зображенням деяких двох оригіналів f1 (t) і f2 (t) , то ці оригінали тотожно рівні в точках своєї неперервності.
Приклади |
|
|
1) (t) |
1, |
t 0 , |
|
t 0. |
|
|
0, |
Розв’язання
4
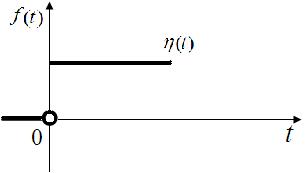
Рис. 2
На графіку наведена функція Хевісайда, яку ще називають одиничною функцією (рис. 2)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
f |
( p) 1 e pt dt lim e pt dt lim ( |
e pt )|b |
|
||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
b |
0 |
|
|
|
|
|
|
|
b |
p |
0 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
1 |
lim e pt |b0 |
|
1 |
|
lim ( e pb e0 ) |
1 |
, |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
p b |
|
|
|
p b |
|
|
|
|
|
|
|
p |
|
||||||||||
тобто |
|
( p ) |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
f |
, |
в символічному запису: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
p |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
або 1 |
. |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
||||||
2) |
f t e at , |
a const |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Розв’язання |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Задана функція є оригіналом, тоді маємо |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
p e at e pt dt lim |
|
e p a t dt |
|
|
|
||||||||||||||||||||||||
|
|
|
|
f |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
b |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
b |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
b |
|
||
|
|
|
lim |
|
|
|
|
|
e p a |
t | |
|
|
|
|
|
lim e p a t | |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
p |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
b |
|
|
p a |
|
0 |
|
|
|
|
|
a b |
|
|
0 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
1 |
|
|
lim |
e p a b e0 |
|
|
|
|
1 |
|
|
|
, |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
p |
a b |
|
|
|
|
|
|
|
|
p a |
|
|
|
|
|
|||||||||||
Якщо Re p a 0. Таким чином, eat |
|
|
|
1 |
|
Re p Re a . |
|
|||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
f t t |
|
|
|
|
|
|
|
|
|
|
|
|
p |
a |
|
|
|
|
|
||||||||||||
3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
5
Розв’язання
В цьому випадку перетворення Лапласа має вигляд:
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u t |
|
|
|
|
|
|
|
|
|
|
|
|
|
du dt |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
te pt dt lim |
|
te pt |
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
f |
|
|
dv e |
pt |
dt |
|
|
|
|
v |
|
e |
pt |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e pb e0 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
e pt |
|
|
|
|
|
|
|
|
|
1 |
|
|
e pt |b |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
||||||||||||||||||||||||||||||||||||||||
lim |
|
|
|
|
|
|
|b |
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
0 |
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
||||||||||||||||||||
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
тобто |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
t |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
4) |
|
|
|
|
f t t cos(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
Розв’язання |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
За формулами Ейлера |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
eit |
cos t i sin t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e it |
|
cos t i sin t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
eit |
e it |
|
|
2 cos t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos t |
|
eit |
|
e it |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
it |
e |
it |
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
p e pt t |
|
e |
|
|
|
|
|
|
dt |
|
1 |
|
lim t e p i t |
e p i t dt |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
u t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
du dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
dv e p i t |
|
e p i t dt |
v |
1 |
|
e p i t |
|
1 |
|
e p i t |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p i |
|
|
|
|
|
|
|
|
|
|
|
|
|
p i |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p i t |
|
|
|
|
|
p i t |
|
b |
|
b |
|
p i t |
|
|
|
|
|
|
|
p i t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
1 |
|
lim |
t |
e |
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
p i |
|
|
|
|
p i |
|
|
|
|
|
p i |
|
|
|
|
|
p i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
p i t |
|
|
|
|
|
e |
p i t |
|
b |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
e |
p i t |
|
|
|
e |
p i t |
|
|
b |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
lim |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p i |
|
|
|
|
|
|
|
p i |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
2 b |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
0 |
|
|
|
|
|
|
||||||||||||||||
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p i |
|
|
|
|
|
p i |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 p i 2 |
p i 2 |
1 p2 2ip i2 p2 2ip i2 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
2 |
|
|
|
p i |
2 |
|
|
|
|
|
|
|
|
|
p i |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
2 |
p i |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
p i |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
i2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
6

|
|
|
1 |
|
2 p2 2 |
|
p2 1 |
||||||
|
|
|
|||||||||||
|
i 2 1 |
|
|
|
|
|
|
|
, |
||||
2 |
p2 1 2 |
p2 1 2 |
|||||||||||
тобто |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
p |
2 |
1 |
|
|
||||
|
t cos t |
|
. |
||||||||||
|
|
|
|
||||||||||
|
|
|
|
|
p 2 1 2 |
|
|
|
|||||
1. Властивості перетворення Лапласа
Лінійність
Лінійній комбінації оригіналів зображень, тобто , якщо
f1 t f 1 p ,
c1, c2 – сталі числа,
с1 f1 t c2 f2 t c1
відповідає лінійна комбінація
f2 t f 2 p ,
f 1 p c2 f 2 p .
Приклад
Знайти зображення функції |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
f t sin at cos at |
a const . |
|
|
|
|
||||||||||||||
Розв’язання |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Використаємо властивість лінійності |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
e |
iat |
e |
iat |
|
1 |
|
1 |
|
|
|
1 |
|
|
|
a |
|
|
a |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
sin at |
|
|
|
|
|
|
|
|
|
|
|
|
, |
sin at |
. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
2i |
|
|
|
|
|
|
|
|
|
|
|
p ia |
|
|
p2 a2 |
|
|
p2 a2 |
||||
|
|
|
|
|
|
|
|
2i p ia |
|
|
|
|
|
||||||||||||
Аналогічно одержуємо формулу для cosat : |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos at |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
p2 |
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
a p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отже , f t |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
p2 a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
7
Подібність |
|
|
|
|
|
|
|
||
|
|
|
|
1 |
|
|
|
p |
|
|
|
|
|
||||||
Якщо f t f p і 0 , то |
f t |
|
|
f |
|
, |
|||
|
|
||||||||
|
|
|
|
|
|
||||
тобто, множення аргументу оригіналу на додатне число призводить до ділення зображення та його аргументу на це число.
Приклад
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|||||
Нехай cos t |
|
|
|
|
. |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
p2 1 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
p |
тут |
1 a . |
||||
|
|
|
|
|
|
a |
|
|
|
|
|||||||||
Тоді cos at |
|
|
|
|
|
|
|
|
|
||||||||||
|
a |
p 2 |
|
|
p2 |
a2 |
|||||||||||||
|
|
1 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|||||
Зміщення |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Якщо f t |
|
|
p , |
a const , |
|
|
|||||||||||||
f |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
то eat f t |
|
|
|
p a , |
|
|
|
|
|
||||||||||
f |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тобто множення оригіналу на функцію eat тягне за собою зміщення змінної |
|||||||||
p Re p a S0 . |
|
|
|
||||||
Приклад |
|
|
|
|
|
|
|
|
f t e 2t cos 3t |
Знайти зображення функції |
|
||||||||
Розв’язання |
|
|
|
|
|
||||
|
|
|
p |
|
|
|
|||
Маємо cos 3t |
|
|
. |
За властивістю зміщення ( a 2 ) |
|||||
|
|
|
|||||||
|
|
|
|||||||
|
p2 9 |
|
|
||||||
|
|
|
|
|
|
p 2 |
|
|
|
e2t cos 3t |
|
|
|
|
|
|
|
|
. |
|
p |
2 2 |
|
|
|||||
|
|
9 |
|||||||
Запізнювання |
|
|
|
||||||
|
|
|
|
|
|
p , |
|
|
|
Якщо f (t) |
|
|
f |
|
0, |
||||
|
|
|
|
то f t |
|
p , |
|
e p |
f |
||
|
|
|
|
8
тобто |
запізнювання оригіналу |
|
на |
|
додатню |
|
величину |
|
призводить до |
||||||||||||||||||||||||||||||||||||||
множення зображення оригіналу без запізнювання на |
|
e p . |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
Приклад |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (t) t 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Знайти зображення функції |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
Розв’язання |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f1 t t , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Якщо вважати , що задана функція |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
то t 1 можна уявити як |
|
f1 t 1 t 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
Тоді зображення різниці |
t 1 одержуємо за допомогою властивості |
|||||||||||||||||||||||||||||||||||||||||||||
запізнювання. Маємо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
f1 t t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
e pt |
t dt lim |
e |
pt t dt |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
b |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
u t |
|
|
|
|
|
|
|
|
|
|
|
du dt |
|
|
|
|
|
|
|
t e pt b |
|
e pt b |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
dv e |
pt |
|
|
|
|
|
|
|
|
|
v |
e |
|
|
|
lim |
|
|
|
|
|
p |
|
|0 |
|
2 |
|0 |
|
|
||||||||||||||||
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b e |
pb |
|
|
e |
pb |
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
2 |
, |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
p |
p |
p |
|
|
p |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
тобто |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||||||||||
|
|
f |
|
t |
t |
|
, |
|
|
|
|
f |
|
t 1 t 1 e p |
. |
|
|||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p 2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Диференціювання оригіналу |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f t |
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Якщо |
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f n t є оригіналами, то |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
і функції f t , |
f t , , |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
f t |
|
|
|
|
|
p f 0 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
p |
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
f t |
|
|
p2 |
|
|
|
|
p p f 0 f 0 , |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f t |
|
|
|
p3 |
|
|
|
|
p p2 f 0 p f 0 f 0 , |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
f |
|
|
|
(А) |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.......... .......... .......... .......... .......... .......... .......... .......... .......... . |
||||||||||||||||||||||||||||||||||||||||||||||
|
f n t |
|
|
|
|
|
|
p pn1 f 0 f n1 0 . |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
pn |
f |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
9

Зауваження
Розглянута властивість диференціювання оригіналу разом із властивістю лінійності широко використовується при розв’язанні лінійних диференціальних рівнянь.
Приклад. Знайти зображення виразу:
y t 2y t 3y t 2y t 2,
якщо |
|
|
|
|
|
|
|
|
|
y 0 3, |
y 0 0, |
y 0 2. |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Розв’язання |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Нехай y t |
|
y p y . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тоді, на підставі формул (А) , маємо |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
y t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
p y 3, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
y t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
p 2 y p 3 0, |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
p3 y p 2 3 p 0 2, |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 2 1 |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Отже , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y t 2 y t 3y t 2 y t 2 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
p3 y 3 p 2 2 2 p 2 y 3 p 3 p y 3 2 y |
|
|||||||||||||||||||||||||||
|
p |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p p3 2 p 2 |
3 p 2 3 p 2 6 p |
2 |
11. |
|
|
|||||||||||||||||||
|
|
|
y |
|
|
||||||||||||||||||||||||
|
|
|
|
p |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Диференціювання зображення
Якщо f t f p , то
10
