ОСВІТИ І НАУКИ,

МОЛОДІ ТА СПОРТУ УКРАЇНИ

ОДЕСЬКИЙ

НАЦІОНАЛЬНИЙ МОРСЬКИЙ УНІВЕРСИТЕТ

Кафедра „Вища та прикладна математика”

ФУНКЦІЇ КІЛЬКОХ ЗМІННИХ

Методичні вказівки до практичних занять

Одеса – 2012

Методичні вказівки розроблені –- старшим викладачем кафедри „Вища та прикладна математика” Одеського національного морського університету.

Методичні вказівки схвалено кафедрою „Вища та прикладна математика” ОНМУ (протокол № ).

Рецензент: ст. викл. каф. В та ПМ

Диференціальне числення функцій кількох змінних.

Множини точок числового простору.

Означення. Упорядкована послідовність дійсних чисел називається точкою – вимірного числового простору . Числа називаються координатами цієї точки. Точка позначається . Для просторів (площина) і (тривимірний простір) користуються частіше позначеннями відповідно і .

Відстань між точками і позначається і визначається рівністю

. (9.1)

Означення. околом даної точки називається множина тих точок , для яких

. (9.2)

окол точки будемо позначати .

Проколеним околом точки називається множина точок , для яких

(9.3)

(тобто множина всіх точок за винятком самої точки ). Проколений окол позначимо .

Зокрема в двовимірному просторі околом точки є внутрішність круга радіуса з центром у точці , а у тривимірному просторі – внутрішність

кулі радіуса з центром у точці .

Означення. Нехай деяка множина точок . Точка називається внутрішньою точкою множини , якщо існує такий окіл точки , усі точки якого належать до . Точка містить у собі як точки множини , так і точки, що не належать до .

Означення. Множина називається (внутрішньою) областю, якщо вона задовольняє вимоги:

1. усі точки є внутрішніми точками;

2. будь – які дві точки 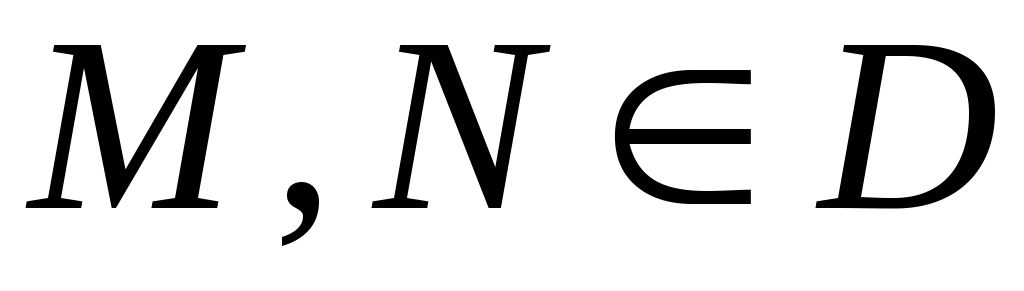можна сполучати суцільною кривою, всі точки якої належать до 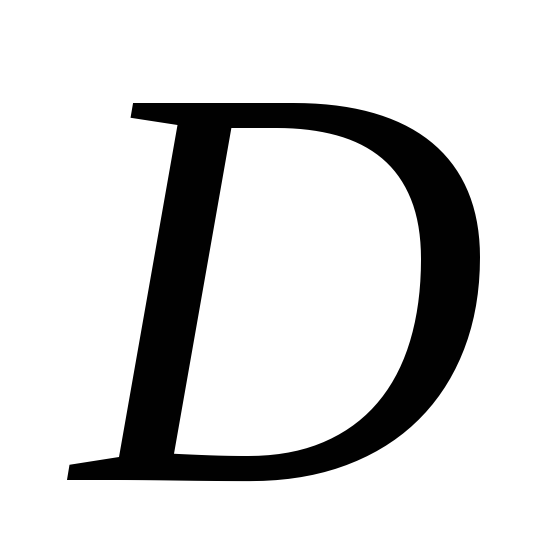(умова зв’язності).

Область разом із своїми межовими точками називається замкненою і

позначається .

Множина межових точок області називається її межею.

Зокрема в двомірному просторі область являє собою деяку плоску фігуру, а її межа – лінію, яка цю фігуру обмежує (контур фігури). У тривимірному просторі область – просторове тіло, а її межа – поверхня , що обмежує це тіло.

У одновимірному просторі (на числовій прямій) областю є числовий інтервал, який можна задати чи описати двома способами: або вказуючи його межу (наприклад ), або за допомогою нерівностей (наприклад ). Подібним чином і в просторі область можна задати, вказавши її межу або за допомогою нерівностей, що визначають межі, в яких змінюються координати точок, належних до області.

Приклади. 1. Область обмежена лініями і . Визначимо її за допомогою нерівностей (рис. 9.1).

Р И С. 9.1 !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!11

Знайдемо точки перетину ліній:

.

Отже проекцією області на вісь є інтервал , або . Для кожного значення ордината точок області знаходиться в межах від до . Таким чином задана область визначається нерівностями

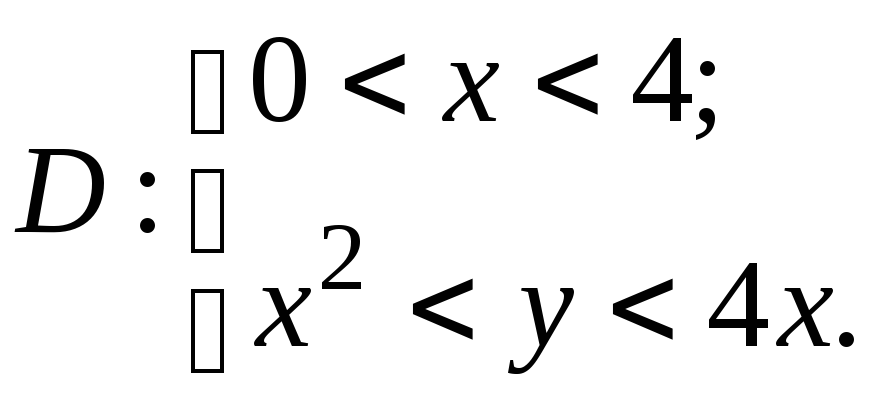
Зазначимо, що проекцією даної області на вісь є , а для кожного абсциса точок області знаходиться в межах від до . Значить дана область визначається і такими нерівностями:

.

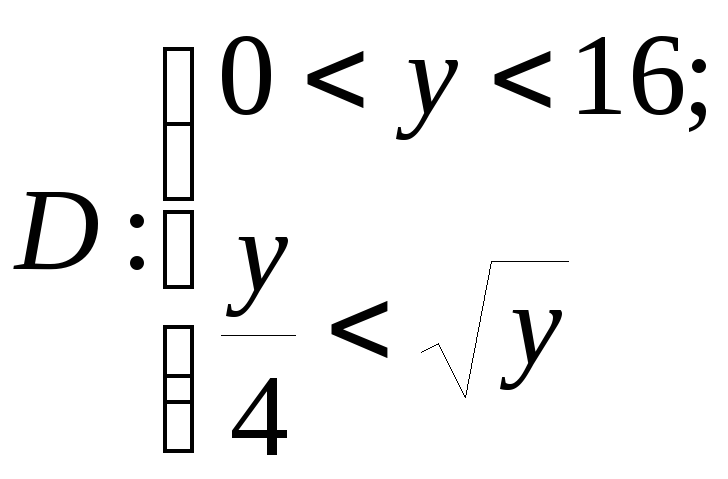Зауваження. В межових точках області відповідні нерівності переходять у рівності, отже коли потрібно задати замкнену область, то в описанні області слід замінити строгі нерівності нестрогими. Так, у попередньому прикладі замкнена

область визначається нерівностями

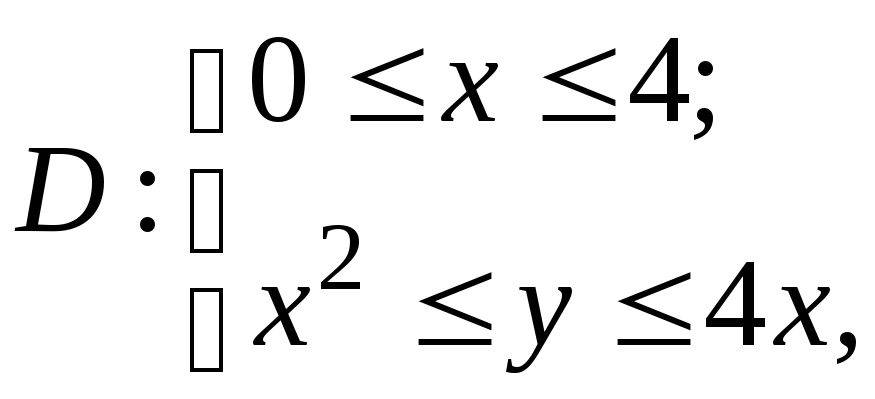або

2. Область задана нерівностями

Знайти межу області і зобразити її на рисунку.

Р И С. 9.2 !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Рівняння межі області отримаємо, змінивши нерівності в означенні області рівностями:

Таким чином межа області складається з двох прямих: і які проходять через початок координат і ділять площину на 4 кути: (рис. 9.2). Залишається перевірити, які з цих кутів належать до даної області. Для цього беремо координати довільної точки в даному куті і перевіряємо, чи задовольняють вони визначальні нерівності області:

а) точка лежить у куті ; нерівності виконуються, отже , а значить і вся внутрішність кута належить до заданої області;

б) точка лежить у куті ; її координати визначальну нерівність не задовольняють, отже точки всередині кута не належить до області .

Аналогічним чином переконуємося, що внутрішність кута належить, а внутрішність кута не належить до області .

Таким чином задана область складається з точок кутів і , включаючи межові точки (точки сторін цих кутів), тобто є замкненою (рис. 9.2).