Задачи Матюнин / УМФ 4(2)

Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего образования

Пермский национальный исследовательский политехнический университет

Факультет Аэрокосмический 

Специальность 24.05.02 Проектирование авиационных 

и ракетных двигателей 

Специализация Проектирование авиационных двигателей 

и энергетических установок 

Кафедра Авиационные двигатели 

Дисциплина «Уравнения математической физики» Отчёт о решении задачи №4

На тему	Задача об одномерном
нестационарном течении в сжимаемой среде

Студенты	Гамов Антон Сергеевич	(		)
	Петров Кирилл Олегович	(		)
	Похлебаев Георгий Юрьевич	(		)
Группа	АД-16-2с

Принял

(

доц. каф. АД Матюнин В.П.

)

Дата:

Пермь 2018 г.

ЗАДАНИЕ

Определить скорость волны в одномерном нестационарном течении в сжимаемой среде.

ВВЕДЕНИЕ

Следует пояснить для точности дальнейших действий, каким является течение. Течения, параметры которых зависят от времени и одной координаты, называют одномерными нестационарными течениями. Газ называют сжимаемым, если в потоке газа происходит заметное изменение плотности. Таким образом, при движении среды будут изменяться как по координате, так и по времени её скорость, давление и плотность.

1. Физическая модель

Распространение звуковых волн в пространстве является одним из примеров нестационарного течения. Движение происходит не посредством перемещения среды, а передачей возмущения. Скорость этого возмущения в разные стороны от источника имеет разное значение. В то же время и сам источник может двигаться с определённой скоростью. Поэтому следует учесть, что полная скорость состоит из скорости источника и скорости распространения возмущений. Такая модель имеет большой недостаток – большое количество внешних возмущений, влияющих на распространение волн от источника.

Поэтому удобнее в качестве физической модели выбрать жидкую среду, движущуюся в длинном канале. На этом канале, установлен компрессор, создающий направленное движение частиц.

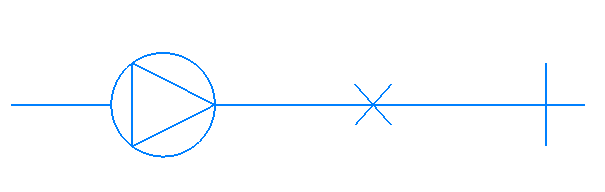
Рис.1. Канал с возмущением в потоке

Рис.2. Скачок давления в трубе при её местном расширении

Труба имеет модуль упругости, поэтому может расширяться. В результате расширения увеличивается давление, происходит гидроудар. Вследствие чего происходит изменение скорости, плотности и давления потока. Таким образом, появляется внутреннее возмущение.

2. Математическая модель

Используя уравнения состояния, уравнения сохранения массы, импульса (количества движения) и энергии, описывающие одномерное нестационарное течение идеального сжимаемого газа, можно записать в следующем виде:

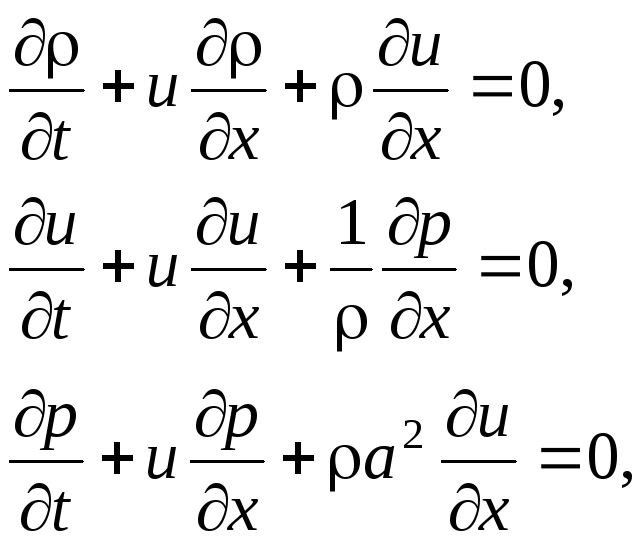(2.1)

где u – скорость источника возмущений, a – скорость возмущений. Необходимо принять, что течение энергоизолированное изоэнтропное, тогда , где – показатель адиабаты. На основании этого условия, система решается с тремя неизвестными:.

Для формулировки краевых условий используется метод характеристик. Суть его заключается в том, что для построения области определенности некоторого отрезка начальной прямой t = 0, нужно через концы этого отрезка провести характеристики волнового уравнения. Область определенности заключена между правой характеристикой, проходящей через левый конец отрезка начальной прямой, левой характеристикой, проходящей через правый конец отрезка, и самим отрезком прямой.

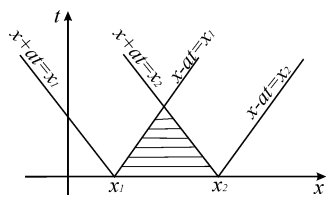
Рис.1. Область определённости отрезка [x₁, x₂]

3. Решение

Для решения используется квазилинейная система:

(3.1)

Чтобы применить уравнение (3.1) к решению данной задачи, следует произвести некоторые преобразования системы (2.1).

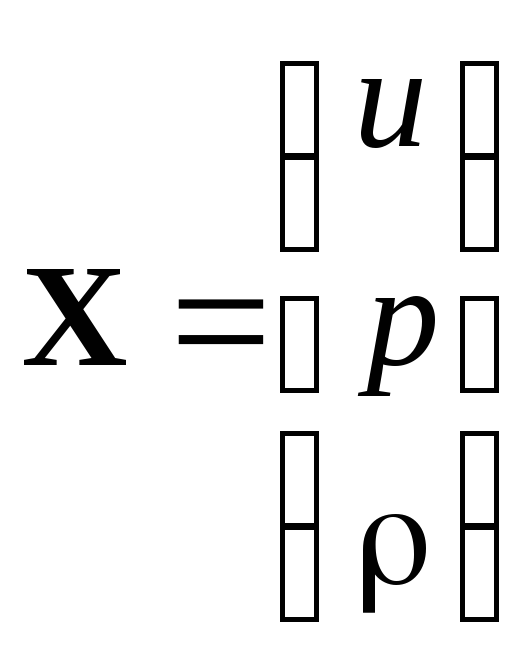- матрица неизвестных функций; (3.2)

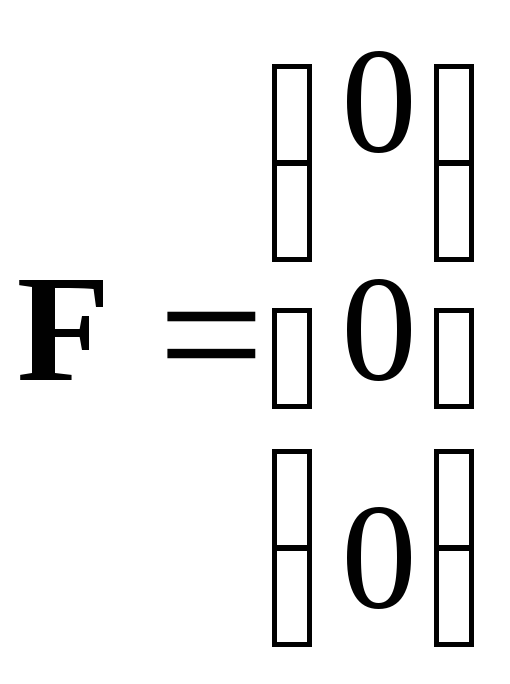- свободные члены. (3.3)

Для удобства записи матриц и оперирования с ними надо записать развёрнуто:

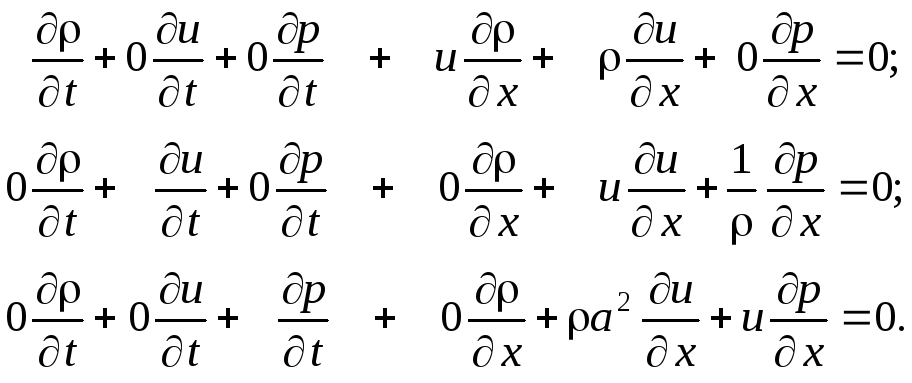, (3.4)

Частные производные по t относятся к матрице A, по x к B. Тогда матрицы A и B имеют вид:

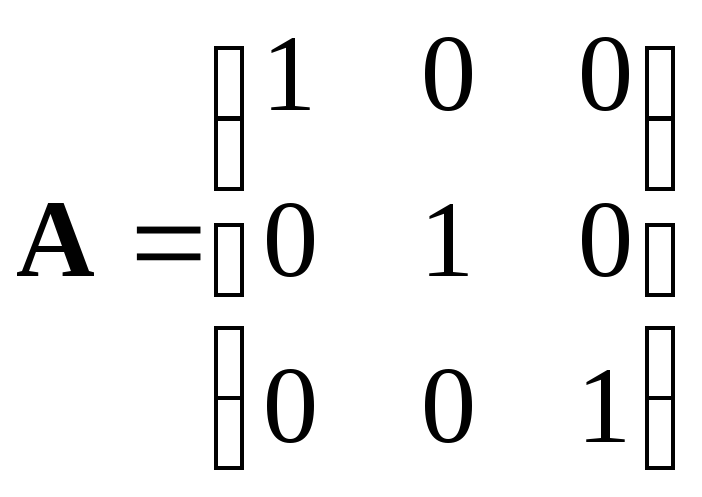; (3.5)

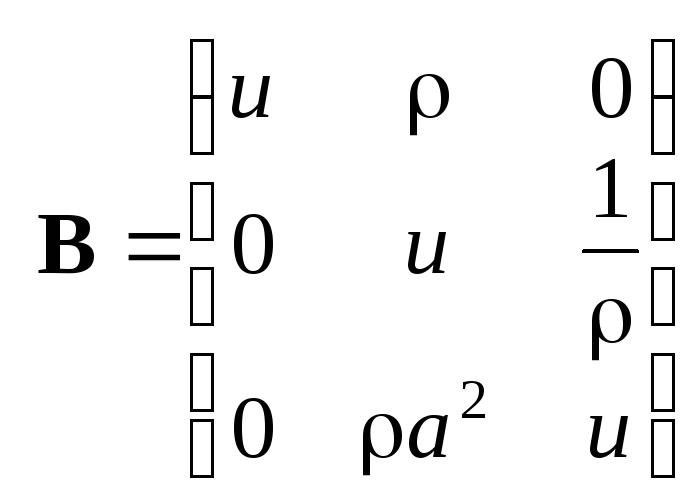. (3.6)

Записывается выражение для дифференциала и выражается из него :

; (3.7)

. (3.8)

Подставляя уравнение (3.8) в (3.1):

; (3.9)

. (3.10)

Если скобка в левой части выражения (3.10) тождествен­но равна нулю, из предположения о существовании решения си­стемы (3.7) следует, что производные X/x и X/t определяются неоднозначно. Кривая, вдоль которой существуют решения, в этом случае называется характе­ристикой.

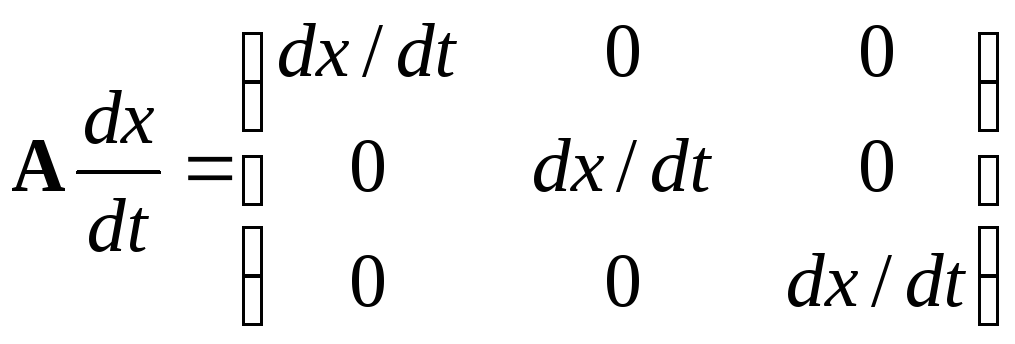; (3.11)

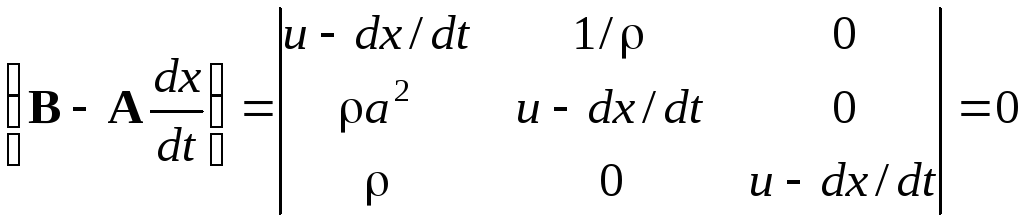; (3.12)

; (3.13)

; (3.14)

. (3.15)

Из уравнения (3.15) следует, что существует три решения:

- характеристика x₀; (3.16)

- характеристика x_-; (3.17)

- характеристика x₊; (3.18)

Выражения (3.17) и (3.18) являются инвариантами Римана.

Источник движется со скоростью u, возмущения со скоростью a.

a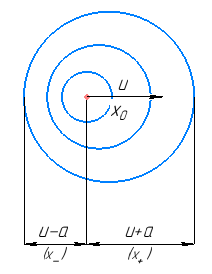

Рис. 2. Распространение характеристик х волны

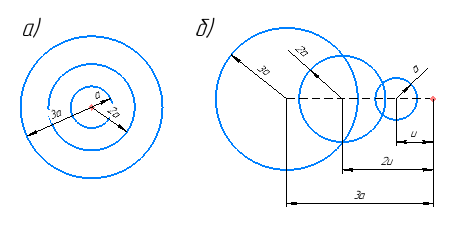
Рис. 3. Схема скоростей для волн а) при нулевой скорости перемещения возмущений; б) при не нулевой скорости перемещения возмущений

4. Частное решение

В матрице (3.12) следует заменить любой столбец на . При замене первого или второго столбца происходит потеря корней, поэтому следует произвести это действие с третьим столбцом.

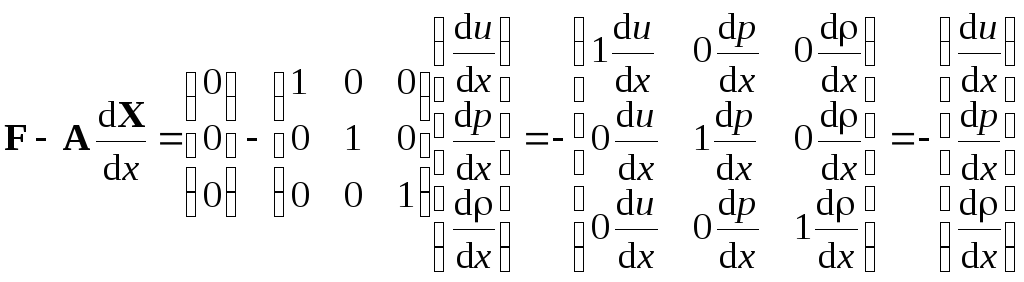. (4.1)

Тогда формула (3.12) с подстановкой матрицы (4.1) будет иметь вид:

. (4.2)

По правилу вычисления определителя можно получить решение (4.2):

;

;

. (4.3)

Подставив вместо в уравнение (4.3) решение , можно получить результат:

. (4.4)

Решению, полученному в уравнении (4.4), соответствует - нулевое условие совместности характеристик.

Подставив вместо в уравнение (4.3) решения, полученные в формулах (3.17) и (3.18), можно получить результат:

;

;

. (4.5)

На основании уравнения (4.5) можно выразить два решения:

- решению соответствует - характеристика плюс;

- решению соответствует - характеристика минус.

Если течение изоэнтропическое, то выражение (4.5) является полными дифференциалами величин I_, которые называются инвариантами Римана, выраженными формулой (4.6). Инварианты Римана являются решением уравнений, описывающих одномерное нестационарное движение.

(4.6)

При изоэнтропическом движении параметры являются определенными функциями от p, и поэтому стоящие в формуле (4.6) интегралы имеют определенный вид.

Т.к. рассматривается идеальный адиабатный процесс, то уравнение адиабаты будет иметь вид;

.

(4.7)

где k – показатель адиабаты (отношение удельных теплоемкостей).

Необходимо решить интеграл из уравнения (4.6). Для этого нужно преобразовать произведение в знаменателе :

,

, (4.8) 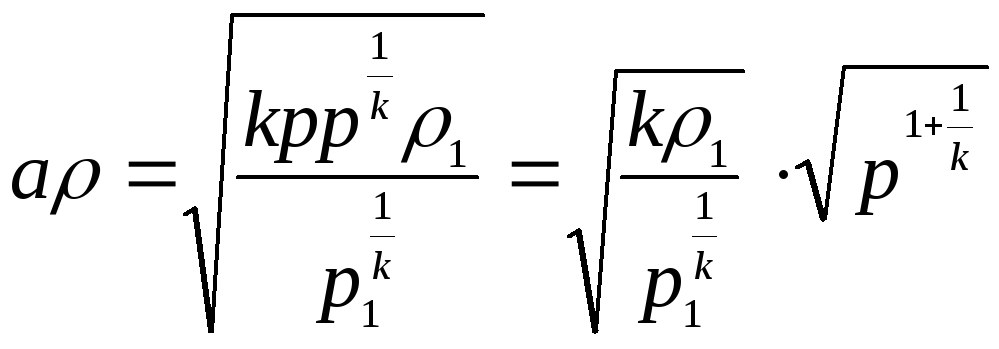. (4.9)

Вид интеграла после подстановки в него формулы (4.9):

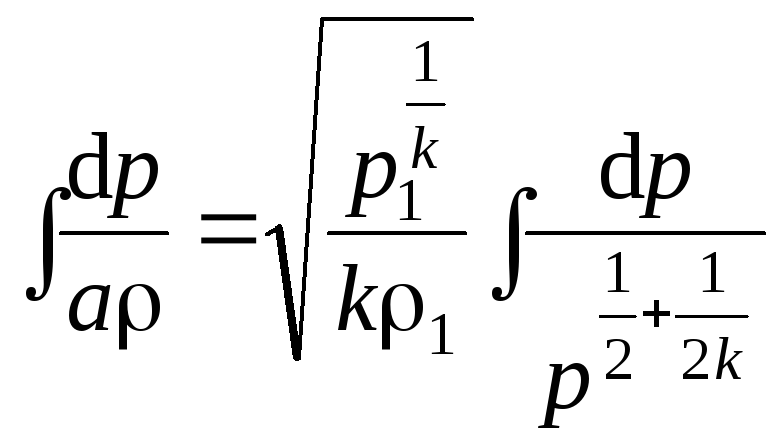. (4.10)

Рассмотрение интеграла без константы, вынесенной из него:

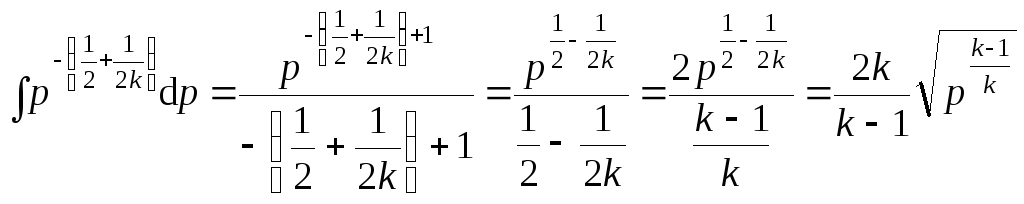. (4.11)

Подстановка результата интеграла в формулу (4.10):

. (4.12)

Учитывая, что:

, (4.13)

можно получить выражение:

. (4.14)

После подстановки результата интеграла , выраженного формулой (4.14), в уравнение (4.6), оно примет вид:

. (4.15)

5. Анализ достоверности решения

Используя плоскость x, t, можно построить примерный вид характеристических линий:

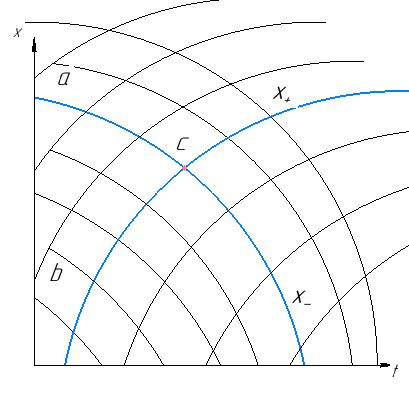
Рис. 4. Характеристические линии

Для конкретного нахождения параметров в некоторой точке сетки необходимо располагать начальными условиями. Определить параметры в точках позволяет метод Эйлера, суть которого заключается в замене дифференциальных уравнений на уравнения в разностном виде.

;

;

, ;

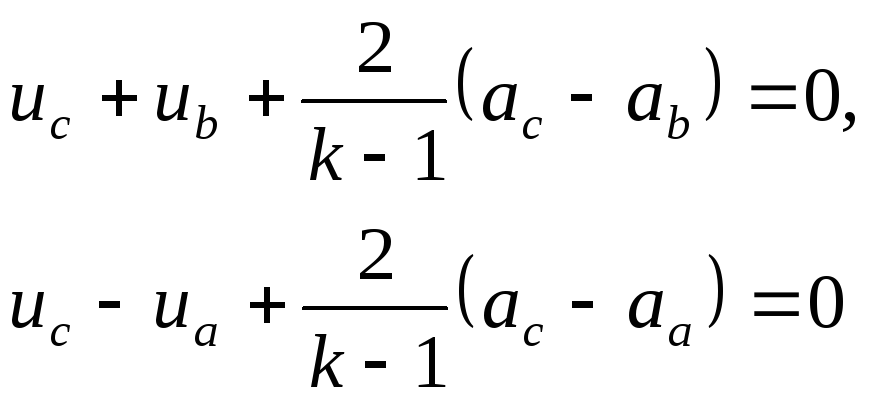(5.1)

Этот способ имеет большую погрешность, поэтому используют схему Эйлера с пересчетом, учитывающую влияние производной. В качестве первого приближения в данном методе используется само исходное значение.

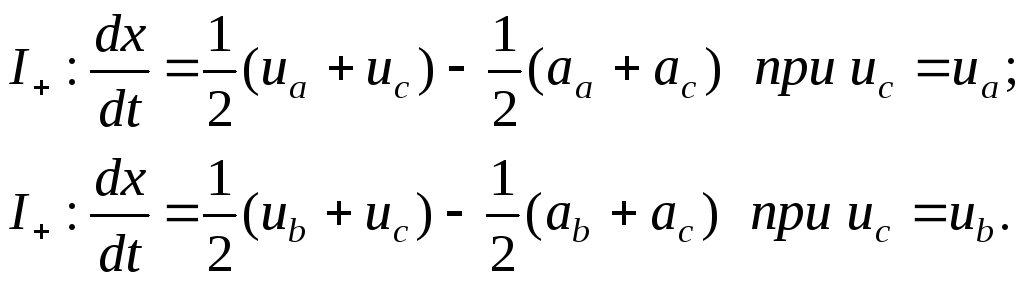
Для подтверждения достоверности решения можно рассмотреть автомобиль, движущийся сначала к наблюдателю, затем удаляющийся от него с той же скоростью и в том же направлении. При приближении звук более высокочастотный, так как происходит сжатие волн согласно рис. 2, затем он приобретает низкочастотный характер, так как происходит разряжение. При сжатии длина волны уменьшается, частота соответственно увеличивается, и, наоборот, при разряжении.

Вывод

Волны разной природы происхождения ведут себя с физической стороны одинаково. Как для звуковой потока, так и для жидкостного вслед за возмущением будет происходить изменение параметров волны. Характеристики волны однозначно определяют её поведение при нарушении потока. При гидроударе в трубе возникает резкое увеличение давления и снижение скорости в данной точке, поэтому необходимой задачей является вычисление максимальной скорости, с которой поток будет идти равномерно. Проведённые в данной задаче вычисления и конкретно полученные инварианты Римана играют важную роль в гидрогазодинамике.

10