Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего образования

Пермский национальный исследовательский политехнический университет

Факультет Аэрокосмический 

Специальность 24.05.02 Проектирование авиационных 

и ракетных двигателей 

Специализация Проектирование авиационных двигателей 

и энергетических установок 

Кафедра Авиационные двигатели 

Дисциплина «Уравнения математической физики» Отчёт о решении задачи №4

На тему	Задача об одномерном
нестационарном течении в сжимаемой среде

Студенты	Гамов Антон Сергеевич	(		)
	Петров Кирилл Олегович	(		)
	Похлебаев Георгий Юрьевич	(		)
Группа	АД-16-2с

Принял

(

доц. каф. АД Матюнин В.П.

)

Дата:

Пермь 2018 г.

ЗАДАНИЕ

Определить скорость волны в одномерном нестационарном течении в сжимаемой среде.

ВВЕДЕНИЕ

Следует пояснить для точности дальнейших действий, каким является течение. Течения, параметры которых зависят от времени и одной координаты, называют одномерными нестационарными течениями. Газ называют сжимаемым, если в потоке газа происходит заметное изменение плотности.

1. Физическая модель

Распространение звуковых волн в пространстве является одним из примеров нестационарного течения. Движение происходит не посредством перемещения среды, а передачей возмущения. Скорость этого возмущения в разные стороны от источника имеет разное значение. В то же время и сам источник может двигаться с определённой скоростью. Поэтому следует учесть, что полная скорость состоит из скорости источника и скорости распространения возмущений.

В подтверждении выбора такой модели можно рассмотреть автомобиль, движущийся сначала к наблюдателю, затем удаляющийся от него с той же скоростью и в том же направлении. При приближении звук более высокочастотный, затем он приобретает низкочастотный характер.

2. Математическая модель

Используя уравнения состояния, уравнения сохранения массы, импульса (количества движения) и энергии, описывающие одномерное нестационарное течение идеального сжимаемого газа, можно записать в следующем виде:

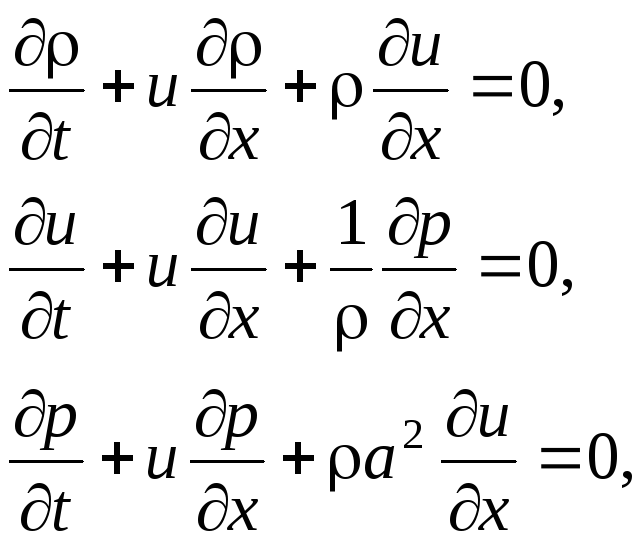(2.1)

где u – скорость источника возмущений, a – скорость возмущений. Система имеет три неизвестные функции: , u, p.

Для формулировки краевых условий используется метод характеристик. Суть его заключается в том, что для построения области определенности некоторого отрезка начальной прямой t = 0, нужно через концы этого отрезка провести характеристики волнового уравнения. Область определенности заключена между правой характеристикой, проходящей через левый конец отрезка начальной прямой, левой характеристикой, проходящей через правый конец отрезка, и самим отрезком прямой.

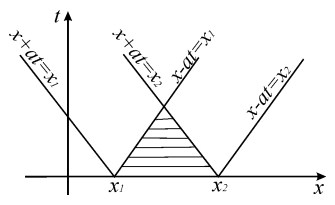
Рис.1. Область определённости отрезка [x₁, x₂]

3. Решение

Для решения используется квазилинейная система:

(3.1)

Чтобы применить уравнение (4.1) к решению данной задачи, следует произвести некоторые преобразования системы (2.1).

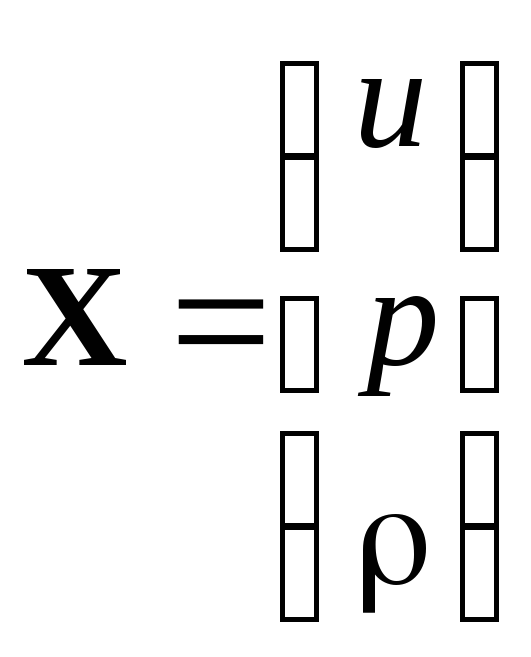- матрица неизвестных функций; (3.2)

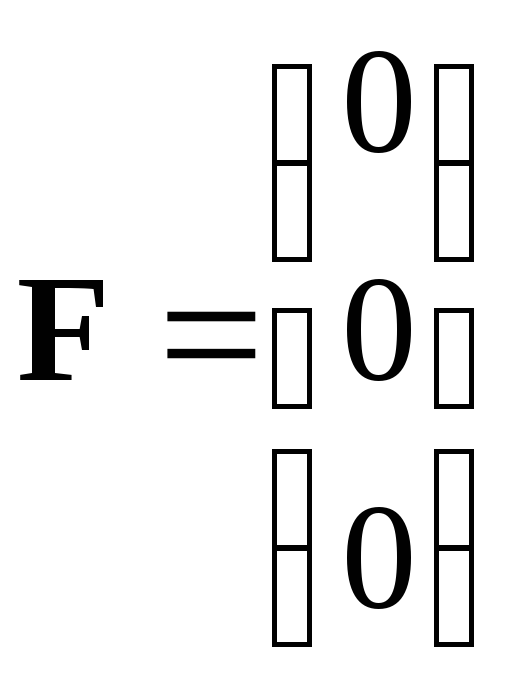- свободные члены. (3.3)

Для удобства записи матриц и оперирования с ними надо записать развёрнуто:

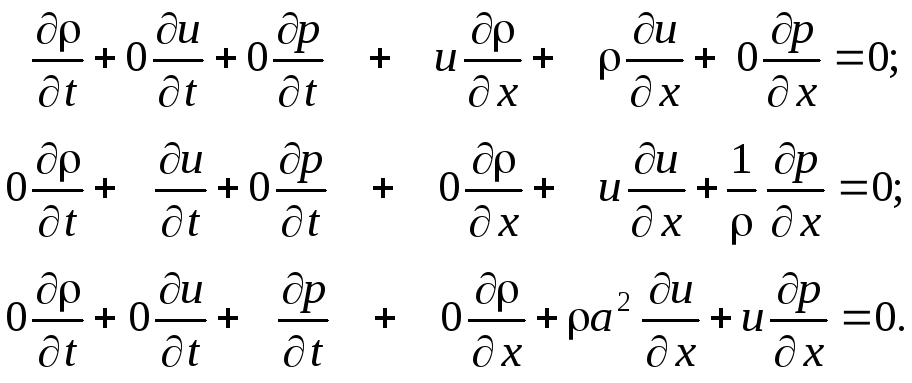, (3.4)

Частные производные по t относятся к матрице A, по x к B. Тогда матрицы A и B имеют вид:

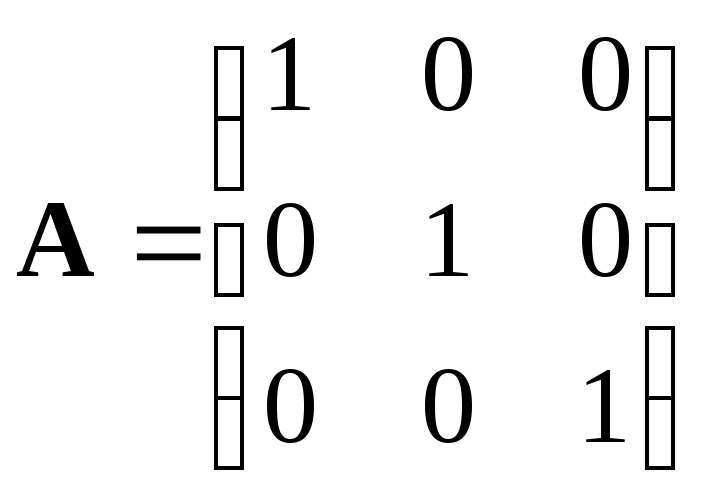; (3.5)

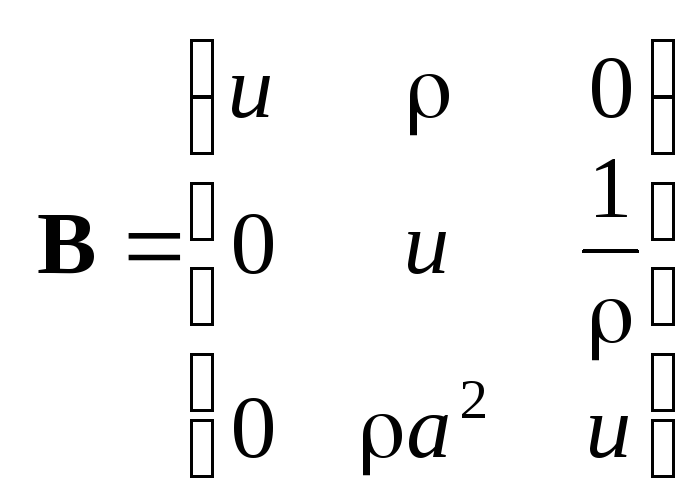. (3.6)

Записывается выражение для дифференциала и выражается из него :

; (3.7)

. (3.8)

Подставляя уравнение (3.8) в (3.1):

; (3.9)

. (3.10)

Если скобка в левой части выражения (3.10) тождествен­но равна нулю, из предположения о существовании решения си­стемы (3.7) следует, что производные X/x и X/t определяются неоднозначно. Кривая, вдоль которой существуют решения, в этом случае называется характе­ристикой.

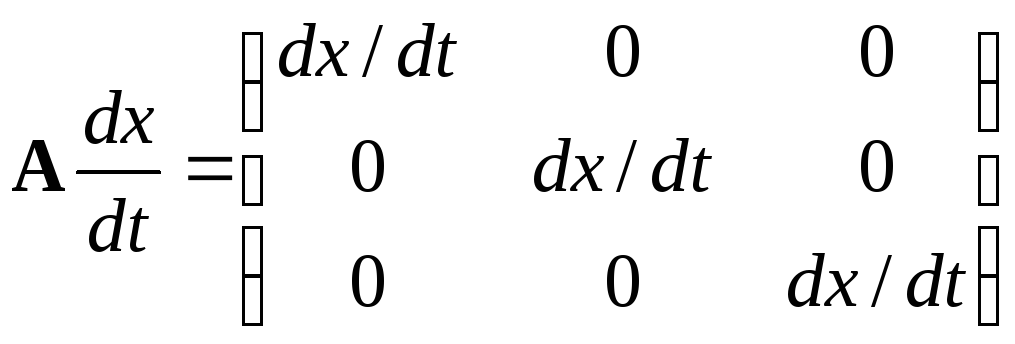; (3.11)

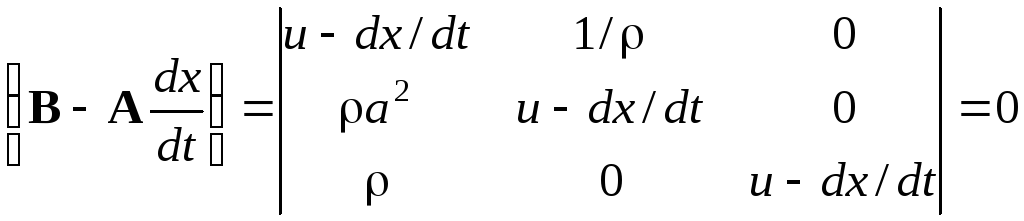; (3.12)

; (3.13)

; (3.14)

. (3.15)

Из уравнения (3.15) следует, что существует три решения:

- характеристика x₀; (3.16)

- характеристика x_-; (3.17)

- характеристика x₊; (3.18)

Выражения (3.17) и (3.18) являются инвариантами Римана.

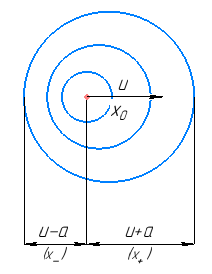
Рис. 2. Распространение характеристик х звуковой волны

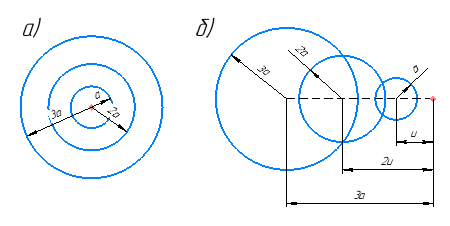
Рис. 3. Схема скоростей для звуковых волн а) при нулевой скорости перемещения звуковых волн; б) при не нулевой скорости перемещения звуковых волн

Таким образом, оговоренное в физической модели явление, исходя из рис. 2, можно объяснить тем, что за источником волны сгущаются и звук становится более высокочастотным, перед – происходит разряжение, звук низкочастотный.

4. Анализ достоверности решения

Вывод

5