Лекции краткий курс Сопромат Иовенко 2011

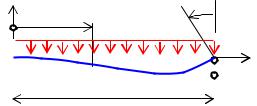
6

d 3 w

=

1

dM

=

Qy

x

,

dz3

E I x

dz

E I x

d 4 w

=

1

dQy

= −

q

.

dz 4

E I x

dz

E I x

Каждая производная имеет четкий физический смысл и четкую математическую запись. А в дифференциальном уравнении упругой линии, записанном в виде

d 4 w	= −	q
dz 4		E I x

нагрузка q известна. При интегрировании уравнения необходимо задать четыре граничных условия (по два на каждом конце балки) в том числе так называемые силовые граничные условия – условия, накладываемые на силовые величины (изгибающий момент и поперечную силу), которые выражаются через производные от прогиба.

Рассмотрим два характерных примера определения перемещений в простых статически неопределимых балках при изгибе.

Пример 3. Имеем балку, жестко заделанную в левом концевом сечении и свободно опертую на другом конце, загруженную равномерно распределенной нагрузкой интенсивностью q (рис. 9.6). Найдем угол поворота сечения С (αc ).

	y	z1	α
			q

С

B

L

z

Рис. 9.6

В нашем случае имеем при z = 0

w(0)

= 0 и α(0) = 0 , при z = L

w(L) = 0 и M x (L) = 0 .

Удовлетворяя дифференциальные зависимости при изгибе

граничным условиям:

q z

d 4 w

= −

q

,

d 3 w

= −

q

∫ dz + C = −

+ C ,

E I x

dz3

dz 4

E I x

E I x

d 2 w

= −

q z 2

+ C z + D ,

dw

= −

q z3

+ C

z 2

+ D z + G ,

2

dz 2

2 E I x

dz

6 E I x

w = −

q z 4

+ C

z3

+ D

z 2

+ G z + H ,

24

E I x

2

6

7

получим w(0) = 0 или H = 0,

α(0) = 0

или

G = 0,

0 = −

q L4

+ C

L3

+ D

L2

0 = −

q L

2

+ C

L

+ D ,

или

24

E I x

6

2

12 E

I x

3

M x (L)

=

d 2 w

= −

q L2

+ C L + D = 0 .

dz 2

E I x

2

E I x

Решая последние два уравнения относительно интегрирования C и D получим

−

q L2

+ C

L

+ D = 0

C = −

5 q L

12 E I

8 E I

x

3

,

x .

q L2

q L2

−

+ C L + D = 0

D = −

2 E I x

8 E I x

w(L) = 0 или

M x (L) = 0 или

постоянных

Тогда, угол поворота сечения С (αc ) будет равен

dw

q L3

5 q L

L2

q L2

q L3

αc =

= −

+ (

)

+ (−

) L =

.

dz

6 E I x

8 E I x

2

8 E I x

48 E I x

Пример 4. Рассмотрим балку, жестко заделанную в левом концевом сечении и свободно опертую на другом конце, нагруженную как показано на рис. 9.7. Найдем угол поворота сечения С (αc ).

y

z1

М

α

z

B

L

С

Рис. 9.7

Граничные условия остаются прежними: при z = 0

w(0) = 0 и

α(0) = 0 , при z = L

w(L) = 0 .Изменится только граничное силовое условие –

при z = L

M x (L) = −M .

Удовлетворяя дифференциальные зависимости при изгибе

граничным условиям и учитывая, что q = 0,

E I x

d 4 w

= 0 ,

E I x

d 3w

= C ,

E I x

d 2 w

= C z + D ,

dz3

dz 4

dz 2

E I x α = E I x

dw

= C

z 2

+

D z + G , E I x w = C

z3

+ D

z 2

+ G z + H ,

dz

2

6

2

получим

w(0) = 0

или H = 0, α(0) = 0 или G = 0,

w(L) = 0 или

0 = C

L3

+ D

L2

или

0 = C

L

+ D ,

M x (L) = −M или

6

2

3

8

M x

= E I x

d 2 w

,

E I x

d 2 w

= C z + D ,

C L + D = −M .

dz 2

dz 2

Решая последние два уравнения относительно постоянных

интегрирования C и D получим

L

C = −

3 M

C

+ D = 0

,

2 L

.

3

M

C L

+ D = −M

D =

2

Тогда, угол поворота сечения С (αc ) будет равен

3 M L2

M

M L

αc = −

M L

E I x αc = (−

)

+ (

)

L

= −

,

.

2 L

2

2

4

4 E I x

Вопросы для самопроверки

1.Что называется балкой?

2.Что называется прямым изгибом?

3.Какие внутренние силовые факторы возникают в сечении балки при поперечном изгибе?

4.Какие правила знаков приняты для поперечной силы и изгибающего момента?

5.Что называется жесткостью поперечного сечения при изгибе?

6.Какие перемещения получают поперечные сечения балок при прямом изгибе?

7.Чему равна кривизна оси балки при чистом изгибе?

8.Почему точное дифференциальное уравнение изогнутой оси балки можно заменить приближенным уравнением?

9.Какая дифференциальная зависимость существует между прогибами и углами поворота сечений балки?

10.Как из приближенного дифференциального уравнения изогнутой оси балки получаются выражения углов поворота и прогибов ее сечений?

11.Из каких условий определяются постоянные интегрирования, входящие в уравнение углов поворота и прогибов сечений балки?

12.Запишите дифференциальные зависимости при изгибе?

13.Какие балки называются статически неопределимыми?

14.Какой вид дифференциального уравнения упругой линии используется при определении перемещений в статически неопределимых балках?

15.В каком порядке производится определение перемещений методом непосредственного интегрирования дифференциального уравнения упругой линии?

16.В каких случаях удобно пользоваться при определении перемещений методом непосредственного интегрирования дифференциального уравнения упругой линии?

17.Сколько граничных условия необходимо задать при определении перемещений в статически неопределимых балках?

9

1

Лекция № 10

Продольный изгиб прямого стержня

Понятие об устойчивости

Соблюдение условий прочности и жесткости еще не гарантирует способ- ности конструкции выполнять предназначенные ей функции. Так система при некотором значении нагрузки может потерять устойчивость своего начального состояния.

Под устойчивостью понимается свойство системы сохранять свое состоя- ние при внешних воздействиях. Если система таким свойством не обладает, она называется неустойчивой. В равной мере можно сказать, что неустойчивым является и ее состояние.

При потере устойчивости реализуется переход к некоторому новому положению равновесия, что в подавляющем большинстве случаев сопровожда- ется большими перемещениями, возникновением пластических деформаций или полным разрушением.

Наиболее простым случаем является потеря стержня устойчивости цент- рально сжатого стержня (рис. 10.1). При достаточно большой силе стержень не может сохранять прямолинейную форму (рис. 10.1, а) и неминуемо изогнется. Произойдет потеря устойчивости (рис. 10.1, б или рис. 10.1, в).

F	Fкр
	C1	y	w
L	L		Fкр
			z
	L 2
			z
	y		L
а	б		в

Рис. 10.1

Значение силы, нагрузки, напряжения, при котором первоначальная фор- ма равновесия упругого тела становится неустойчивой, называется соответ- ственно критической силой, критической нагрузкой и критическим напряже- нием.

Продольный изгиб

Потерю устойчивости прямолинейной формы равновесия центрально сжатого прямого стержня часто называют продольным изгибом, так как она влечет за собой значительное искривление стержня под действием продольной силы.

2

Термин «проверка на продольный изгиб» является условным, так как здесь речь идет не о проверке на изгиб, а о проверке на устойчивость прямоли- нейной формы стержня.

Это наиболее простая и в то же время одна из наиболее важных инженер- ных задач, связанных с проблемой устойчивости.

Формула Эйлера

Рассмотрим прямой стержень постоянного сечения с шарнирно закреп- ленными концами, нагруженный на верхнем конце центрально приложенной сжимающей силой F (рис. 10.1, а).

Наименьшее значение центрально приложенной сжимающей силой F , при котором прямолинейная форма равновесия стержня становится неустойчи-

вой, называется критической силой ( Fкр ).

Для ее определения отклоним стержень в положение, показанное пункти- ром, и установим, при каком наименьшем значении силы F = Fкр стержень мо-

жет не вернуться в прежнее положение (рис. 10.1, б или рис. 10.1, в). Т.е. рас- смотрим условия, при которых возможно равновесие стержня с изогнутой осью.

Заметим, что сама постановка задачи иная, чем во всех ранее рассмотрен- ных отделах курса. Если раньше мы определяли деформацию стержня при заданных внешних нагрузках, то здесь ставится обратная задача: задавшись искривлением оси сжатого стержня, следует определить, при каком значении осевой сжимающей силы F такое искривление возможно.

Координаты точек упругой линии стержня обозначим через z и w (рис. 10.1, в). Начало координат считаем расположенным у нижнего конца стержня, а ось z направленной вверх (рис. 10.1, б).

При малых прогибах, приближенное дифференциальное уравнение упру- гой линии имеет вид

EI d 2 w = M . dz 2

Изгиб стержня происходит в плоскости минимальной жесткости, и поэто- му под величиной I понимается минимальный момент инерции сечения.

Изгибающий момент в сечении с абсциссой z равен

M = −Fкр w

Подставим выражение M в уравнение упругой линии

	d 2 w	+	Fкр w	= 0	или	d 2 w	+ k 2 w = 0 , где	k 2 =	Fкр	.
	dz 2		EI min			dz 2			EI min
Интеграл полученного дифференциального уравнения имеет вид
				w = C1 sin kz + C2 cos kz .
Это решение заключает в себе три неизвестных: постоянные интегриро-
вания C1 и C2 и значение k ,					так как величина критической силы пока нам
неизвестна.

	3
Произвольные постоянные C1	и C2 подбираются так, чтобы были удов-
летворены граничные условия: при	z = 0 w = 0 и при z = L и w = 0 . Из

первого условия вытекает, что C2 = 0 .

Таким образом, изогнутая ось стержня является синусоидой с уравне- нием w = C1 sin kz .

Второе условие дает

C1 sin kL = 0 .

Это уравнение имеет два возможных решения: либо C1 = 0 , либо же sin kL = 0 .

Если C1 = 0 , то перемещения w обращаются тождественно в нуль, и стержень, следовательно, имеет прямолинейную форму. Это противоречит ис- ходным предпосылкам нашего вывода. Следовательно, sin kL = 0 , и величина kL может иметь следующий бесконечный ряд значений:

kL = 0 , π , 2π , 3π , … , π n ,

где n – произвольное целое число.
Таким образом, имеем kL = π n или k = π n L . С учетом k 2 = Fкр		EI	min
получаем
F = π 2 EI min n2 .
кр	L2

Иначе говоря, нагрузка, способная удержать слегка искривленный стер- жень в равновесии, теоретически может иметь целый ряд значений. Наимень- шее значение осевой сжимающей силы, при которой становится возможным продольный изгиб, будет при n = 1. Тогда

F = π 2 EI min .

кр L2

Эта формула впервые была получена академиком Петербургской Акаде- мии наук Л. Эйлером в 1744 году, поэтому первую критическую силу Fкр назы-

вают также эйлеровой критической силой для сжатого стержня с шарнирно- опертыми концами.

Анализ формулы Эйлера

Значению этой критической силы соответствует изгиб стержня по сину-

соиде

w = C1 sinπ zL .

Здесь мы видим, что константа C1 в выражении для упругой линии оста- лась неопределенной. Перемещения найдены, как говорят, с точностью до по- стоянного множителя. Физическое значение ее выяснится, если в уравнение синусоиды положить z = L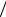2 , тогда w = C1 . Значит, C1 – это прогиб стержня в сечении посредине его длины (рис. 10.1, б).

Так как при критическом значении силы F равновесие изогнутого стерж- ня возможно при различных отклонениях его от прямолинейной формы, лишь

4

бы эти отклонения были малыми, то естественно что, прогиб w = C1 остается неопределенным.

Значениям критической силы высших порядков Fкр = π 2 n2 EI min L2 со-

ответствуют искривления по синусоидам с двумя, тремя и т.д. полуволнами – w = C1 sinπ n zL (табл. 10.1).

Таким образом, чем больше точек перегиба будет иметь синусоидально- искривленная ось стержня, тем больше должна быть критическая сила.

						Табл. 10.1
n	Fкр			w		форма равновесия
1	π 2 EImin	L2	C1	sinπ z L
2	4π 2 EImin	L2	C1	sin 2π z L
3	9π 2 EImin	L2	C1	sin 3π z L

Считается, что формы равновесия при n ≥ 2 неустойчивы и возможны лишь при наличии промежуточных опор в сечениях с нулевым прогибом.

Влияние способа закрепления концов стержня

Найденное значение критической силы справедливо лишь для стержня с шарнирно-опертыми концами и изменится при других условиях закрепления концов стержня.

Закрепление сжатого стержня с шарнирно-опертыми концами мы будем называть основным случаем закрепления. Другие виды закрепления будем при- водить к основному случаю.

Если повторить весь ход вывода для стержня, имеющего другие условия закрепления концов стержня, то полученные другие значения критической силы можно объединить с формулой для критической силы основного случая и записать их в следующем виде:

F =	π 2	EI	min .
кр	(µ L)2
Здесь – так называемый коэффициент приведения длины, (µ L) – приведен-
ная длина стержня. Можно сказать, что –		число, показывающее, во сколько

следует увеличить длину шарнирно-опертого стержня, чтобы критическая сила для него равнялась критической силе стержня длиной L в рассматриваемых условиях закрепления.

Понятие о приведенной длине было впервые введено профессором Петербургского института инженеров путей сообщения Ф. Ясинским.

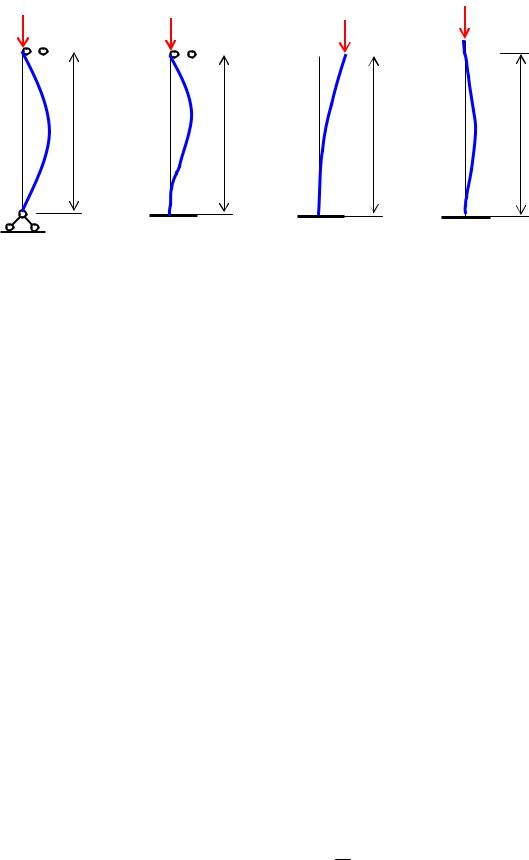
На рис 10.2 показаны четыре наиболее часто встречающиеся случая закре-пления стержня и указаны соответствующие значения коэффициента приведе-ния длины. В двух последних случаях значение легко определяется

5

путем простого сопоставления упругой линии изогнутого стержня с длиной полу-волны синусоиды при шарнирном закреплении.

Fкр

Fк

Fкр

Fкр

р

L

L

L

L

= 1,0

= 0,7

= 2,0

= 0,5

Рис. 10.2

На практике, однако, почти никогда не встречаются в чистом виде те закрепления концов стержня, которые мы имеем на наших расчетных схемах.

Так в конструкциях очень часто встречаются сжатые стержни, концы которых приклепаны или приварены к другим элементам. Такое закрепление, однако, трудно считать защемлением, так как части конструкции, к которым прикреплены эти стержни, не являются абсолютно жесткими. Достаточно возможности уже небольшого поворота опорного сечения в защемлении, чтобы оно оказалось в условиях, очень близких к шарнирному опиранию. Поэтому на практике недопустимо рассчитывать такие стержни, как стойки с абсолютно защемленными концами.

Коэффициент запаса устойчивости

Допускаемой нагрузкой называется нагрузка, определяемая по формуле

	F = [F ] =	Fкр	,
		nу
	доп

где nу – коэффициент запаса устойчивости, который принимается таким, чтобы была обеспечена надежная работа стержня.

Условие устойчивости

Критическая сила Fкр вызывает в сжатом стержне критические напряже-

ния σ кр , которые являются опасными для него. Поэтому, чтобы обеспечить

устойчивость прямолинейной формы стержня, сжатого силой F , необходимо к условию прочности

σ ≤ [σ ] или FA ≤ [σ ] добавить еще условие устойчивости:

6

σ ≤ [σ у ] или	F	≤ [σ у ] , где [σ у ] =	σ кр		, где σ		=	Fкр	(или Fкр = σ кр A ).
	A					кр		А
			n	у

Для возможности осуществить проверку на устойчивость мы должны показать, как определять σ кр и как выбрать коэффициент запаса nу .

Заметим, что при составлении условия устойчивости, вводится в расчет площадь брутто, т.е. без учета его ослаблений ( A = Aбр ).

Это объясняется тем, что ослабление сечения стержня заклепками или болтами в металлических конструкциях, врубками в деревянных происходит не по всей его длине, а лишь на отдельных небольших участках. Сопротивление же стержня выпучиванию зависит от жесткости стержня на всем его протяже- нии. Поэтому местные ослабления практически не влияют на величину крити- ческой силы.

Критические напряжения

Критические напряжения можно представить в следующем виде:

σ кр =	Fкр	=	π 2 EI min	,
			(µ L)2 A
	A

	где с учетом imin2 =	I min	и λ = L получаем
		A
			imin		π 2 E .
			σ кр	=
					λ2

Здесь imin – наименьший радиус инерции сечения, λ – гибкость сжатого стерж- ня.

Безразмерная величина λ играет весьма важную роль во всех проверках сжатых стержней на устойчивость. Она учитывает одновременно четыре характеристики сжатого стержня:

1) длину стержня; 2) величину площади сечения: 3) способ закрепления его концов, 4) форму сечения, зависящую от imin .

Вид графической зависимости σ кр от λ показан на рис. 10.3. Эта зави-

симость представляется гиперболической кривой, так называемой «гиперболой Эйлера».

σ кр

Гипербола

Эйлера

λ = L

imin

Рис. 10.3