Контрольная работа ОДМиТА вариант 10

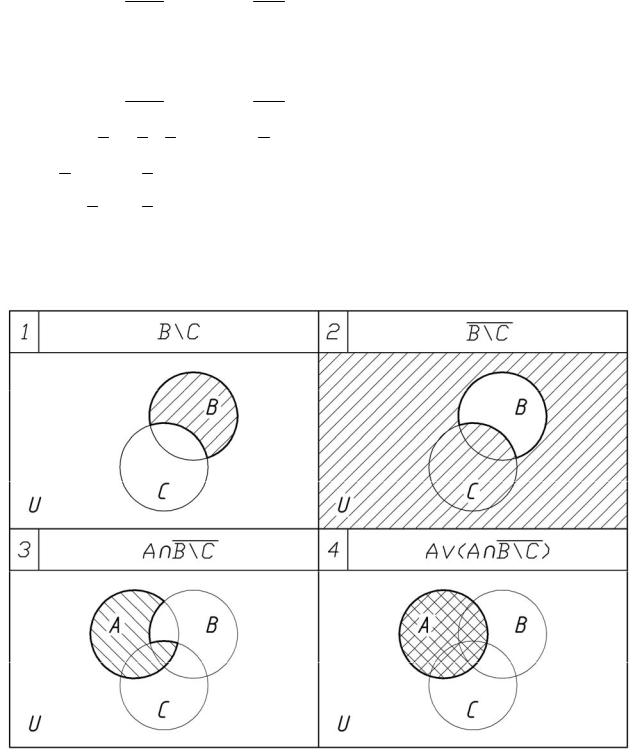
Контрольная работа №1 Вариант №10

Задание №1

Докажите тождество через тождественные преобразования и с помощью диаграмм Эйлера-Венна.

((A \ C) A C) ∩ (A (A ∩ B \ C)) = A \ C

Решение:

((A \ C) A C) ∩ (A (A ∩ B \ C)) = A \ C

((A ∩ C) ( A ∩ C)) ∩ A = A ∩ C

C ∩ A = A ∩ C

A ∩ C = A ∩ C , что и требовалось доказать.

Иллюстрация справедливости равенства на диаграммах Эйлера-Венна

2

3

Задание №2

Получить СДНФ, СКНФ, используя таблицу истинности. Построить ДНФ, КНФ, упростив выражение S = A → B C ↔ B C → A C .

Решение:

Построим таблицу истинности высказывания, заданного формулой:

A	B	C	B C		A	→ B C	B	C		A C	B	C	→ A C	S
0	0	0	0		0		1			0	0			1
0	0	1	0		0		0			0	1			0
0	1	0	0		0		1			0	0			1
0	1	1	1		1		1			0	0			0
1	0	0	0		1		1			0	0			0
1	0	1	0		1		0			1	1			1
1	1	0	0		1		1			0	0			0
1	1	1	1		1		1			1	1			1

Согласно алгоритмам построения СДНФ и СКНФ по таблице истинности получим следующие результаты:

СДНФ = ABC ABC ABC ABC

СКНФ = (A B C )(A B C )(A B C )(A B C )

Построим булево выражение, эквивалентное заданной формуле и найдем ДНФ и КНФ:

A → B C = A (B C ) = A (B C ) = ( A B) ( A C )

B C → A C = (B C ) ( A C ) = (B C ) ( A C ) = (B C ) ( A C ) = = (C A) (C B) = C (A B)

4

(

)

( A

B) ( A C )

↔ C

A

B

=

{

}

{

(

) }

(

)

=

( A B) ( A C )

C

A

B

( A B) ( A C )

C

A

B

=

={( A B) ( A C ) C (A B)} { ( A B) ( A C ) C (A B) }=

={( A B) (A B) C (C A)} { (A B) (A C ) C (A B) }=

={A C} { A (B C ) (C A) (C B) }=

={A C} {A (B C ) (A C ) (B C )}=

={A C} {A (A C ) (B C ) (B C )}=

={A C} {A C}

ДНФ = ( A C ) (A C )

КНФ = ( A C ) (A C ) = ( A C ) A ( A C ) C = (A C ) (A C )

5

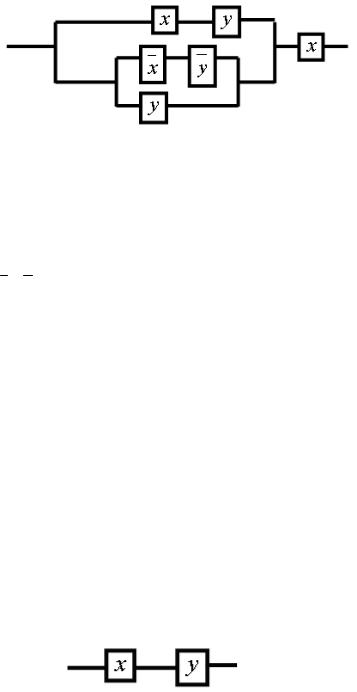
Задание №3

Упростить схему:

Решение:

Построим функцию проводимости данной схемы, которая будет задаваться таблицей истинности для релейно-контактной схемы:

f = (x y) (x y) y x

x	y	(x y)	(				)	(x y) (				)	(x y) (				) y	f
				x		y			x		y			x		y
0	0	0	1					1					1					0
0	1	0	0					0					1					0
1	0	0	0					0					0					0
1	1	1	0					1					1					1

По данной логической функции построим СДНФ:

СДНФ = xy

Построим более простую схему, имеющую ту же функцию проводимости, что и исходная:

6

Задание №4
Выяснить,	каким		из		пяти		замкнутых	классов
(T0 ,T1 , L, S, M ) принадлежит функция, заданная своим характеристическим
множествомM0 = {001, 011, 111} . Построить полином Жегалкина.
Решение:
Строим таблицу истинности для заданной функции:
		x	y	z	f
		0	0	0	1
		0	0	1	0
		0	1	0	1
		0	1	1	0
		1	0	0	1
		1	0	1	1
		1	1	0	1
		1	1	1	0

Исходя из определения функций, сохраняющих константу 0, выясняем, что f T0 .

Исходя из определения функций, сохраняющих константу 1, выясняем, что f T1 .

Построим для функции f полином Жегалкина:

f = x yz xyz x yz x yz xyz = xz x y xyz =

=(x 1)(z 1) x( y 1) xy(z 1) = (x 1)(z 1) x( y 1) xy(z 1) =

=xz x z 1 xy x xyz xy = z xz xyz

Он имеет нелинейный	вид. Следовательно, f L , где L - класс
линейных функций.
Поскольку условие f (x1	,..., xn)=		(		1 ,...,		n) не выполняется, f S , где S -
		f				x
				x

класс самодвойственных функций.

Исходя из определения монотонности функций, следует, что функция f M , где М - класс монотонных функций.

Ответ: f (M )

7

Задание №5

Найти методом Квайна–Мак-Класски минимальную ДНФ функции, заданной своим характеристическим множеством:

M0 = {0000, 0001,1001, 1000, 0101, 1010, 1101, 1011, 1111, 1110}

Решение:

Строим таблицу истинности для заданной функции:

x1	x2	x3	x4	f
0	0	0	0	0
0	0	0	1	0
0	0	1	0	1
0	0	1	1	1
0	1	0	0	1
0	1	0	1	0
0	1	1	0	1
0	1	1	1	1
1	0	0	0	0
1	0	0	1	0
1	0	1	0	0
1	0	1	1	0
1	1	0	0	1
1	1	0	1	0
1	1	1	0	0
1	1	1	1	0

В СДНФ функции f заменим все конституенты единицы их двоичными номерами:

f = 0010 0011 0100 0110 0111 1100

Образуем группы двоичных номеров. Признаком образования i-й группы является i единиц в двоичном номере конституенты единицы:

Номер группы

Двоичные номера конституент единицы

0---

10010 0100

2 0011 0110 1100

30111

4---

Склеим номера из соседних групп. Склеиваемые номера вычеркнем:

Номер группы		Двоичные номера конституент единицы
0	---
1	001-	0-10	01-0 -100
2	0-11	011-

3----

4----

8

Склеим номера из соседних групп. Склеиваться могут только номера, имеющие звездочки в одинаковых позициях. Склеиваемые номера вычеркнем:

Номер группы	Двоичные номера конституент единицы
0	---
1	0-1- 01-0 -100
2	---
3	---
4	---

Имеем три простых импликанты: 0-1-, 01-0, -100 Строим импликантную матрицу.

Простые		Конституенты единицы
импликанты	0010	0011	0100	0110	0111	1100
0-1-	X	X		X	X
01-0			X	X
-100			X			X

По таблице определяем совокупность простых импликант: 0-1-, 01-0, -100, соответствующих минимальной ДНФ.

Таким образом, минимальная ДНФ имеет характеристическое множество {0-1-, 01-0, -100}, то есть имеет вид:

x1x3 x1x2 x4 x2 x3 x4

9

Задание №6

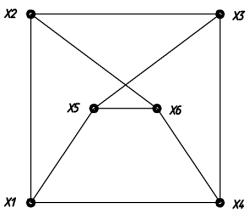
Найти инварианты неориентированного графа, заданного матрицей смежности:

	x1	x2	x3	x4	x5	x6
x1		1		1	1
x2	1		1			1
x3		1		1	1
x4	1		1			1
x5	1		1			1
x6		1		1	1

Решение:

Изобразим граф по заданной матрице смежности:

Инварианты графа: Количество вершин n=6; Количество ребер r=9;

Количество граней f определить невозможно, поскольку граф не является плоским;

Число связности k=2;

Толщина графа для данного графа t(G)=2;

Количество вершин максимальной клики в данном графе равно 2 и поэтому плотность графа q(G)=2.

Найдем наибольшее независимое множество вершин графа. Найдем вершину с наименьшей степенью – х1 (ρ(х1) = 3) и включим ее в независимое множество. Удалим из графа саму вершину х1, смежные ей вершины х2, х4 и

10

х5 а так же инцидентные им ребра х1х2, х1х4, х1х5, х2х3, х2х6, х3х4, х4х6, х3х5, х5х6. В итоге получим граф вида:

Таким образом, мы получили наибольшее независимое подмножество {х1, х3, х6} и соответственно число независимости графа α0 (G) = 3.

Найдем наименьшее вершинное покрытие. Строим матрицу инцидентности графа:

	x1x2	x1x4	x1x5	x2x3	x2x6	x3x4	x3x5	x4x6	x5x6
x1	1	1	1
x2	1			1	1
x3				1		1	1
x4		1				1		1
x5			1				1		1
x6					1			1	1

Столбец, содержащий наименьшее число единиц (х1х2), покрывает две строки — х1 и х2. Среди них выбираем строку с максимальным числом единиц и включаем в искомое покрытие – это строка х1. Исключаем из матрицы строку х1 и столбцы, которые она покрывает. В результате получаем преобразованную матрицу инцидентности и повторяем заново шаги алгоритма:

	x2x3	x2x6	x3x4	x3x5	x4x6	x5x6
x2	1	1
x3	1		1	1
x4			1		1
x5				1		1
x6		1			1	1

На этом этапе столбец х2х3 задает следующую строку искомого покрытия – х3. Переходим к упрощенной матрице инцидентности:

11