КР 1 ОДМиТА 2012

Министерство образования Республики Беларусь

Учреждение образования

«БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ»

Институт информационных технологий

Специальность: Информационные системы и технологии в экономике. КОНТРОЛЬНАЯ РАБОТА

По курсу «Основы дискретной математики и теории алгоритмов»

Вариант 5

Студент-заочник 1 курса

Группы

№ зачётки:

ФИО:

Адрес:

Тел. моб:

Дата выполнения: 11.12.12

Минск, 2012

Задание 1.

Используя диаграммы Эйлера-Венна, решить задачу:

На кафедре иностранных языков работают 18 преподавателей, из них 12 преподают английский язык, 11 – немецкий, 9-французский; 5 преподавателей преподают английский и немецкий языки, 4 - английский и французский, 3 –немецкий и французский. Сколько преподавателей преподают все три языка? Только два языка?

Решение:

Для решения задачи используются следующие обозначения:

А – множество преподавателей английского языка;

В – множество преподавателей немецкого языка;

С – множество преподавателей французского языка;

U – множество преподавателей.

Диаграмма Эйлера-Венна с учетом введенных обозначений примет следующий вид:

Мощности множеств А, В, С и U равны:

m(A) = m(A B С)+m(A  С)+m(A  B C)+m(A  B C)=12;

m(B) = m(A  B C)+m(A  B С)+ m(A  B C)+ m(A  B C)=11;

m(C) = m(A  С)+ m(A  С)+m(A  B  С)+ m(A  B C)=9;

m(U) = m(A B С)+m(A  B С)+m(A  С)+ m(A  B C)+

+ m(A B  С)+ m(A  B С)+ m(A  B С)=18

Мощности множеств преподавателей двух языков:

m(A B)=m(A  B C)+m(A B C)=5;

m(A C)=m(A   C)+ m(A B C)=4;

m(B C)=(A C)+ m(A B C)=3

С учетом предыдущих формул можно записать:

m(U) = m(A B С)+m(A  B С)+m(A  С)+

m(A  B C)+ m(A B  С)+ m(A  B С)+ m(A B C)=

=m(A)- m(A B  С)- m(A  B C)- m(A B C)+

m(B)- m(A  B С) - m(A  B C)+ m(A B C)+

m(C)- m(A B  С) - m(A  B С) - m(A B C)+

+ m(A  B C)+ m(A B  С) + m(A  B С) + m(A B C)=

=m(A)+m(B)+m(C)-m(A B  C)- m(A B  С)- m(A B  С)-

-2* m(A B C)= m(A)+m(B)+m(C)-[m(A  B) - m(A B C)]-[ m(A  C - m(A B C)]-[m(B  С) - m(A B C)]- 2* m(A B C)=

= m(A)+m(B)+m(C)-m(A  B)-m(A  C) – m(B C)+ m(A B C)=

=12+11+9-5-4-3+m(A  C)=20+m(A  B  С).

Следовательно:

m(U)=20+m(A  B  С)=28m(A  B  С)= -2

Ответ: Задача не имеет решения.

Задание 2

Упростить выражение: A A \B\B

Решение:

A A \B\B

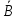  (U  )=U

Ответ:

Задание 3

С помощью ДНФ и КНФ установить выполнимость формулы:

(AB)()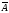

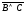Решение:

Разложение формулы:

Ответ: Поскольку полученная формула не удовлетворяет условию теорем 3 и 4, то можно сделать вывод о ее выполнимости.

Задание 4

С помощью совершенных нормальных форм установить, равносильны ли

формулы α и β:

 = A();

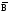
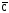 = A.

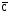
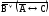Решение:

Построение СДНФ:

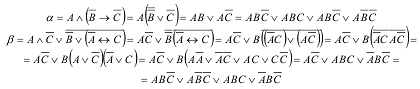
Ответ: Поскольку СДНФ не равны, то формулы α и β не равносильны.

Задание 5

Проверить правильность рассуждения тремя способами:

Если функция непрерывна на данном интервале и внутри его не обращается в ноль, то функция имеет одинаковые знаки на концах данного интервала. Функция имеет одинаковые знаки на концах интервала, но обращается в ноль внутри его. Следовательно, функция разрывна.

Решение:

Посылки и заключения в рассуждении состоят из следующих элементарных высказываний:

А – «Функция непрерывна на данном интервале»;

В – «Функция не обращается в ноль внутри данного интервала»;

С – «Функция имеет одинаковые знаки на концах интервала».

Посылки и заключения:

− A ∧ B → C (посылка Р1);

− C ∧ B (посылка Р2);

− A (заключение Q).

Рассуждение верно, если импликация (A∧ B →C)∧(C ∧ B)→ A тождественно истинна. Для проверки правильности рассуждения строится таблица истины:

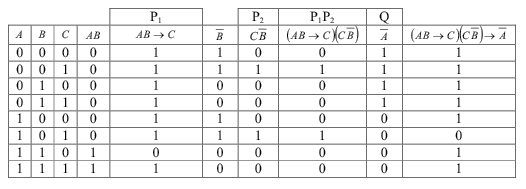
Рассуждение не верно, т.к. полученное значение не является тождественно истинным.

Проверим правильность рассуждения, методом от противного. Для этого заключения Q полагается ложным, т.е. Q = A = 0 , а посылка Р₂ истинной, т.е. P₂= C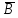= 1. Тогда A =1, C =1, B =1⇒ B = 0. В этом случае посылка Р₁ равна

P₁= A ∧ B → С = 1 ∧ 0 →1=0→1=1. Поскольку ни одна из посылок не приняла значение ложно, то можно сделать вывод, что рассуждение не верно.

Преобразование к равносильной формуле:

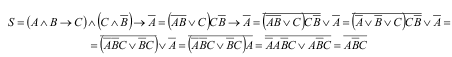
Ответ: Поскольку полученная формула не является тождественно истинной, то рассуждение не верно.

Задание 6

По заданной функции проводимости построить наиболее простую схему:

f(0,1,0)=f(1,1,0)=f(1,1,1)=0

Решение:

Формула алгебры высказываний, имеющую заданную логическую функцию – СДНФ:

Упрощения выражения:

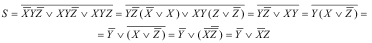
Ответ:

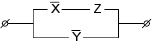
Задание 7

Упростить схему:

Решение:

Соответствующая схеме формула:

Упрощение выражения:

Ответ:

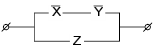
Задание 8

Для заданного графа построить:

1. Матрицу смежности;

2. Матрицу инциденций;

3. Матрицу достижимостей;

4. Найти число внутренней устойчивости, полагая граф неориентированным;

5. Найти число внешней устойчивости, полагая граф неориентированным.

Решение:

Обозначение графа:

Для заданного графа G=(X, Г(X)) множество вершин:

X={X₁, X₂, X₃, X₄, X₅, X₆,}; Г(X₁)={X₂,X₃,X₆}; Г(X₂)={X₃}; Г{X₃}={X₄,X₆}; Г(X₄)={X₅}; Г(X₅)={X₆}; Г(X₆)=.

Матрица смежности:

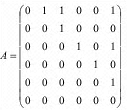
Матрица инциденций:

Поскольку граф не имеет петель, то каждый столбец матрицы В содержит единственный элемент, равный 1 (начало дуги) и единственный элемент равный -1 (конец дуги):

Матрица достижимостей:

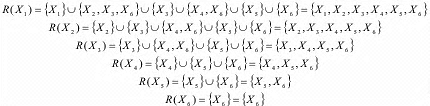
Число внутренней устойчивости:

Внутренне устойчивые множества для заданного графа:

S₁={X₁, X₄};S₂={X₁, X₅}; S₃={X₂, X₄}; S₄={X₂, X₅}; S₅={X₂, X₆};

S₆={X₃, X₅}; S₇={X₄, X₆}; S₈={X₂, X₄, X₆}.

Из них максимальными являются: S₁, S₂, S₄, S₆, S_8.

Следовательно, число внутренней устойчивости равно:

Число внешней устойчивости :

Внешне устойчивые множества для заданного графа

R₁={X₁, X₄, X₆};R₂={X₁, X₃, X₅}; R₃={X₁,X₂,X₄};

R₄={X₁,X₄,X₅}; R₅={X₁,X₄}.

Из них минимальными являются: R₂, R₅. Следовательно, число внешней устойчивости графа равно:

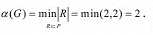
Задание 9

Для графов G₁ и G₂ найти G₁  G₂; G₁  G₂; G₁  G₂.

Решение:

Обозначение графов:

Для заданного графа G₁ = (X₁,Г_I(X)) множество вершин:

X_I= {X₁,X₂,X₃};Г_I(X₁)={X₂}; Г_I(X₂)={X₃}; Г_I(X₃)={X₁}.

Для заданного графа G₂=(X_II, Г_II(X)) множество вершин:

X_II= {X₁,X₂,X₃}; Г_II (X₁)={X₂}; Г_II (X₂)={X₃}; Г_II (X₃)={X₃}.

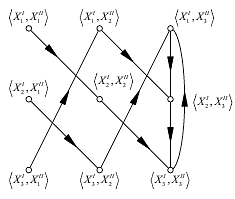
Объединение графов G₁  G₂:

Пересечение графов G₁  G₂:

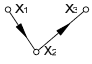
Декартово пересечение графов G₁  G₂: