К.р. ОДМиТА 20 вариант / Sol20

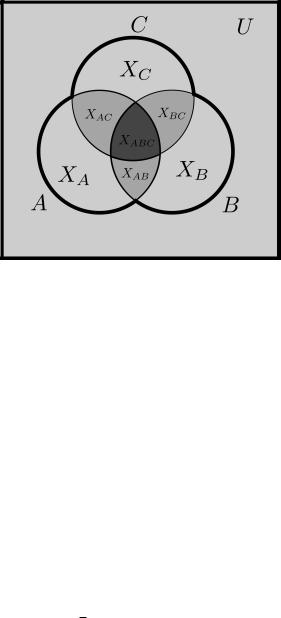
1.20 Прежде чем приступить к решению задачи условимся считать, что княгиня Ростовская не является фрейлиной и соответственно не входит в число ста пятнадцати прибывших на бал фрейлин. Также будем предполагать, что фрейлина не надела никаких подвесок, серьг и колец таких же как у Ростовской тогда и только тогда, когда эта фрейлина не знает о приезде на бал Ростовской.

Пусть универсальным множество U является множество всех приехавших на бал фрейлин. Тогда jUj = 115: Пусть также множество A — это множество всех фрейлин на балу, которые одели подвески а-ля Ростовская, множество B — это множество всех фрейлин одевших серьги от Ростовской и, наконец, множество C — это множество фрейлин на балу, которые носят кольца такие же как у графини.

Рассмотрим диаграмму Эйлера–Венна (рис. 1). Введем следующие обозначения. Пусть множество XA состоит из элементов из U, которые являются элементами множества A и не являются элементами множеств B и C: Пусть множество XB состоит из элементов, которые принадлежат множеству Bn(A[C)

имножество XC = C n (A [ B): Пусть также XAB = (A \ B) n (A \ B \ C); XBC = (B \ C) n (A \ B \ C)

иXAC = (A \ C) n (A \ B \ C):

Рис. 1: Диаграмма Эйлера–Венна

И наконец, пусть XABC = A \ B \ C: По условию задачи jAj = 61; jBj = 65; jCj = 50; jA \ Bj = 36; jA \ Cj = 23; jB \ Cj = 27 и jXABCj = jA \ B \ Cj = 15. Так как jA \ Bj = 36 и jXABCj = 15; то jXABj = jA\Bj jXABCj = 36 15 = 21: По такому же принципу найдем, что jXBCj = jB\Cj jXABCj = 27 15 = 12 и jXACj = jA \ Cj jXABCj = 23 15 = 8:

Затем найдем jXAj; jXBj; jXCj следующим образом:

jXAj = jAj jXABj jXACj jXABCj = 61 21 8		15	= 17	(1)
jXBj = jBj jXABj jXBCj jXABCj = 65 21	12	15	= 17	(2)
jXCj = jCj jXACj jXBCj jXABCj = 50 8	12	15	= 15	(3)
Найдем количество фрейлин jA [ B [ Cj, которые знали, что Ростовская прийдет.
jA [ B [ Cj = jXAj + jXBj + jXCj + jXABj + jXBCj + jXACj + jXABCj =				(4)
= 17 + 17 + 15 + 21 + 12 + 8 + 15 = 97:				(5)

Соответственно множеством фрейлин которые не знали, что Ростовская прийдет является множество

Un (A [ B [ C) и jU n (A [ B [ C)j = 115 97 = 18:

Ответ: 18

2.20 Пусть S = (x ! y) $ (z ! (x $ z)):

Приведем таблицу истинности:

1

x y z	x ! y		z		x $	z		z ! (x $	z	)	S
0 0 0	1	1			0			1			1
0 0 1	1	0			1			1			1
0 1 0	1	1			0			1			1
0 1 1	1	0			1			1			1
1 0 0	0	1			1			1			0
1 0 1	0	0			0			0			1
1 1 0	1	1			1			1			1
1 1 1	1	0			0			0			0

Построим СКНФ по таблице истинности. Функция принимает значения 0 только на двух наборах значений переменных.Составим конституенты нуля: (x _ y _ z) и (x _ y _ z): Следовательно СКНФ имеет вид (x _ y _ z) ^ (x _ y _ z): В свою очередь СДНФ имеет вид (x ^ y ^ z) _ (x ^ y ^ z) _ (x ^ y ^ z) _ (x ^ y ^ z) _ (x ^ y ^ z) _ (x ^ y ^ z):

Найдем ДНФ. Приведем равносильности, которые будут использованы при приведении формулы к ДНФ.

x ! y =					_ y	(6)
				x
x $ y =				_ xy		(7)
	x		y
x _ x y = x						(8)

(x ! y) $ (z ! (x $ z) = (6); (7) = (x ! y) $ (z _ x z _ x z) = (7) =

=(x _ y) (z _ x z _ xz) _ (x _ y)(z _ x z _ xz) = Закон де Моргана и дистрибутивность =

=(x ^ y)(z ^ (x _ z) ^ (x _ z)) _ (x z _ x z _ x x z _ y z _ y xz _ y x z) = (8) =

= x y z(x _ z)(x _ z) _ (x z _ xz _ y z _ y x z) = дистрибутивность =

= x x y z _ xy z z x _ x y z _ x y z z _ (x z _ x z _ y z) = 0 _ 0 _ x y z _ 0 _ x z _ x z _ y z =

= x _ y z _ yz (9)

Построим КНФ:

_

(10)

x

y

z _ yz

= x _ (y _ z) (y _ z) = (y _ z _ x)(y _ z _ x)

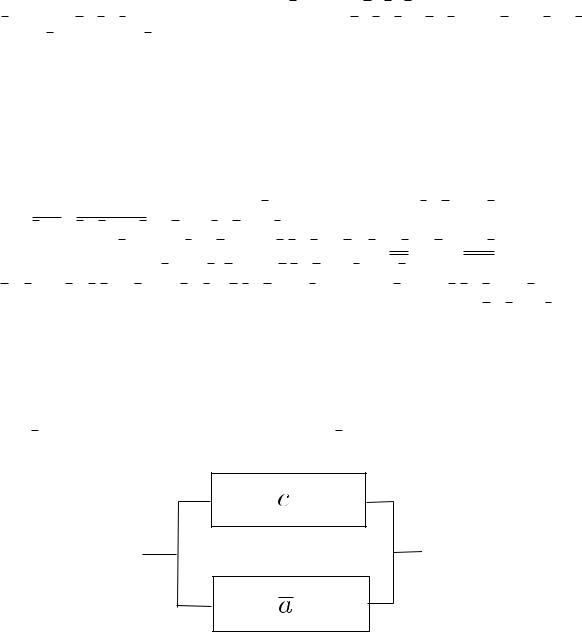
3.20 Учитывая, что дизъюнкция моделируется параллельными соединениями проводников, конъюнкция - последовательным, то формула реализованная этой релейно-контактной схемой запишется как (a _ b)c _ a _ c: Упростим ее и получим эквивалентную c _ a: На рис. 2 изображена соответствующая упрощенная схема.

Рис. 2: Схема

4.20 Построим СДНФ: x y z: Очевидно СДНФ будет полиномом Жегалкина для функции. Отметим, что полином Жегалкина не линеен.

2

Очевидно заданная функция f 2 T0 \ T1 \ M и f 2= S [ L:

1.f 2 T0, поскольку f(0; 0; 0) = 0:

2.f 2 T1; так как f(1; 1; 1) = 1:

3.f 2= L; так как соответствующий полином Жегалкина не линеен.

4.f 2= S; поскольку функция f не самодвойственна. Это видно на примере f(0; 0; 1) 6= f(1; 1; 0): 5.20 Выпишем таблицу истинности функции

	f
0 0 0 0	1
0 0 0 1	0
0 0 1 0	1
0 0 1 1	1
0 1 0 0	1
0 1 0 1	0
0 1 1 0	1
0 1 1 1	1
1 0 0 0	0
1 0 0 1	0
1 0 1 0	0
1 0 1 1	0
1 1 0 0	1
1 1 0 1	1
1 1 1 0	0
1 1 1 1	0

Знаком (*) отметим конъюнкции, которые склеиваются в процессе решения:

0.	0000	00 0	0 0
1.	0010 , 0100	001 ; 0 10 ; 01 0 ; 100	0 1
2.	0011 ; 0110 ; 1100	0 11 ; 011 ; 110
3.	0111 ; 1101

В итоге имеем 4 импликанты: 0 0; 0 1 ; 110 ; 100: Строим импликантную матрицу:

	0000	0010	0100	0011	0110	1100	0111	1101
0 0	1	1	1		1
0 1		1		1	1		1
110						1		1
100			1			1

Следовательно характеристическое множество минимальной ДНФ — f0 0; 0 1 ; 110g и соотвественно минимальной ДНФ является x1 x4 _ x1 x3 _ x1 x2 x3

6.20 Граф G задан матрицей смежности. Изобразим данный граф (рис. 3).

01

	0	1	1	0	1	0	C
B 1		0	1	0	1	0
B	1	1	0	0	1	1	C
B							C
B	0	0	0	0	1	1	C
B							C

BC

@	1	1	1	1	0	1	A
	0	0	1	1	1	0

Рис. 3: Заданный граф G

1. Число вершин n в графе G равно 6.

3

2.Количество ребер m в графе G равно 10.

3.Так как граф G является связным и плоским, то для него справедлива формула Эйлера n m+ f = 2; где n — это число вершин в графе, m число ребер и f число граней. Из формулы следует, что число граней в графе G равно f = m n + 2 = 6:

4.Граф G является связным и следовательно число связности k = 1:

5.Граф G является связным и плоским, поэтому толщина t графа G равна 1.

6.Наибольшую клику в графе G порождает множество вершин fx1; x2; x3; x5g: Cледовательно плотность q(G) графа G равна 4.

7.В графе G множество вершин fx1; x2; x3; x5g порождает клику, поэтому никакие две их них не могут одновременно входить в независимое множество. Множество fx4; x6g также порождает клику, следовательно только одна из вершин x4 или x6 может входить в наибольшее независимое множество.

Следовательно 0(G) = 2:

8.Число вершинного покрытия 0(G) = n 0(G) = 6 2 = 4:

9.Паросочетание которое состоит из ребер fx4; x6g; fx3; x5g; fx1; x2g графа G является наибольшим, так как покрывает все вершины графа G: Следовательно число парасочетания 1(G) = 3:

10.Учитывая, что 1(G) + 1(G) = n; то число реберного покрытия 1(G) = 3:

11.Дополним главную диагональ матрицы смежности графа G единицами. Строка 5 содержит максимальное число единиц и покрывает все столбцы матрицы. Поэтому наименьшее доминирующее множество графа G состоит из одной вершины x5 и следовательно (G) = 1:

12.Плотность графа G равна 4, следовательно (G) 4: На рис. 4 приведена раскраска вершин графа G в четыре цвета a; b; c; d и поэтому (G) = 4:

Рис. 4: Раскраска вершин в 4 цвета

13. Реберно–хроматическое число равно либо (G) либо (G) + 1; где (G) максимальная степень вершин графа G: Заметим, что в нашем случае (G) = 5: На рис. 5 представлена реберная раскраска в 5 цветов a; b; c; d; e. Следовательно реберно–хроматическое число графа G равно 5.

Рис. 5: Реберная раскраска в пять цветов

14. Коцикломатическое число графа (G) — количество ребер любого остовного дерева графа G: Так как (G) = n 1; то (G) = 5:

4

15. Цикломатическое число (G) – это количество ребер, которые необходимо удалить, чтобы получить остовное дерево графа G: Так как (G) = m n + 1; то (G) = 10 6 + 1 = 5:

5