
контрольная по Геометрии и Алгебре №1
.docx
Контрольная работа по Геометрии и алгебре №1
Факультет
НиДо
Специальность
Информатика
Выполнил
студент группы 002021-02
Ефимчик Константин Геннадьевич
Минск 2010
Задача №1
Написать разложение вектора x по трем указанным векторам p, q, r, предварительно проверив, что они образуют базис трехмерного пространства. Координаты векторов:

Решение
Посчитаем
смешанное произведение векторов
 :
:

Следовательно, векторы p,q и r некомпланарные, значит они линейно независимы и образуют базис.
Вектор х можно представить в виде
 или
или
 или
или

Решим полученную систему методом Гаусса:
Ã
=


Последней матрице соответствует следующая система уравнений:

13х3=
– 13
 х3
= -1;
х3
= -1;
х2 = -1 – 2х3 = -1 + 2 = 1;
х1 = 6 – 2х2 = 6 - 2 = 4.
Тогда

Ответ
:

Задача №2
Коллинеарны ли векторы c1 и c2, построенные по двум заданным векторам a и b? Координаты векторов a и b и выражения c1 и c2 через них:
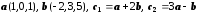 .
.
Решение.
Найдем
координаты векторов
 и
и
 :
:

Векторы
коллинеарны, если пропорциональны
соответствующие координаты. Так как
 ,
то векторы
,
то векторы
 и
и
 неколлинеарны.
неколлинеарны.
Ответ:
векторы
 и
и
 неколлинеарны.
неколлинеарны.
Задача №3
Найти
косинус угла между векторами
 и
и
 .
Координаты точек A,
B
и C:
.
Координаты точек A,
B
и C:
 .
.
Решение
Находим
координаты векторов
 и
и
 :
:

 .
.
Косинус
угла между векторами
 и
и
 найдем
по формуле:
найдем
по формуле:

Ответ:
косинус угла между векторами
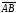 и
и
 0,96
0,96
Задача №4
Вычислить площадь параллелограмма, построенного на векторах a и b. Выражения a и b через векторы p и q:
 .
.
Решение
Площадь
параллелограмма, построенного на
векторах
 и
и
 находится по формуле:
находится по формуле:
 .
.
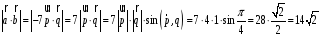
Следовательно,
S
= 14 (квадратных единиц)
(квадратных единиц)
Ответ:
S
= 14 (квадратных единиц).
(квадратных единиц).
Задача №5
Компланарны
ли векторы a,
b
и c?
Координаты векторов a,
b
и c:
 .
.
Решение
Векторы
 компланарны, если их смешанное произведение
равно нулю. Проверим это условие.
компланарны, если их смешанное произведение
равно нулю. Проверим это условие.
 Следовательно,
векторы
Следовательно,
векторы
 компланарны.
компланарны.
Ответ:
векторы
 компланарны.
компланарны.
Задача №6
Исследовать систему
линейных алгебраических уравнений на
совместность и решить 1) методом Гаусса,
2) по правилу Крамера
в случае единственности решения, 3)
матричным методом в случае единственности
решения. Системы уравнений:

1). Решим данную систему методом Гаусса.
Запишем рассмотренную матрицу и с помощью элементарных преобразований над строками матрицы упростим её:

из 2-й строки вычтем 1-ю, умноженную на 2; из 3-й строки вычтем 1-ю, умноженную на 3:

из 3-й строки, умноженной на 7, вычтем 2-ю строку, умноженную на 4:

Последней матрице соответствует следующая система уравнений, эквивалентная исходной:

Из 3-го уравнения получим:

Из 2-го уравнения:

Из 1-го уравнения:

Решение системы:
x1=8; x2=4; x3=2.
2). Решим систему по формулам Крамера:
 ,
,
 и
и
 .
.
Посчитаем определитель системы:

Так как определитель системы Δ отличен от нуля, то система совместна и имеет единственное решение.
Находим
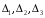 :
:



Тогда,

3). Запишем систему в матричном виде:
АХ=В, где

Решение системы будет:
 где
где
 –
матрица обратная матрице А
–
матрица обратная матрице А
 где
Аij
– алгебраические дополнения элементов
aij
матрицы А.
где
Аij
– алгебраические дополнения элементов
aij
матрицы А.
 из
пункта 2) равно -58.
из
пункта 2) равно -58.
Находим алгебраическое дополнения:

Тогда,

Следовательно,

Решение системы: х1 = 8, х2 = 4, х3 = 2.
Ответ: х1 = 8, х2 = 4, х3 = 2.
Задача №7
На плоскости OXY найти общие уравнения прямых, проходящих через точку пересечения двух прямых перпендикулярно первой и параллельно третьей соответственно. Общие уравнения трех прямых на плоскости OXY даны ниже в соответствии с вариантом. Уравнения двух первых прямых объединены в систему:
 x – 2y – 2 = 0.
x – 2y – 2 = 0.
Решение.
Сначала находим точку пересечения прямых:
 – это
точка пересечения прямых.
– это
точка пересечения прямых.
Запишем
уравнение первой прямой: x+y+1=0.
Уравнение прямой перпендикулярной
первой, имеет вид: x-y+c=0.
Точка М лежит на этой прямой, значит её координаты
должны удовлетворять этому уравнению:
лежит на этой прямой, значит её координаты
должны удовлетворять этому уравнению:
 .
.
Уравнение
прямой принимает вид: x
– y
–
 =
0
=
0
Уравнение прямой, параллельной прямой x – 2y – 2 =0 имеет вид:
x – 2y + C = 0.
Для определения С подставим координаты точки М:

Уравнение прямой принимает вид x – 2y – 1 = 0.
Ответ: Уравнение x – 2y – 1 = 0.
Задача №8
Приведением уравнения к каноническому виду установить, что оно определяет эллипс, гиперболу или параболу. Построить соответствующую кривую 2-го порядка на плоскости OXY. Для эллипса и гиперболы найти полуоси, координаты фокусов, эксцентриситет, уравнения директрис. Найти уравнения асимптот гиперболы. Для параболы найти параметр, координаты фокуса, уравнение директрисы. Уравнения кривых:
3x2 + 4y2 = 12.
Решение.
 ,
разделим на 12:
,
разделим на 12:

 –
каноническое
уравнение эллипса.
–
каноническое
уравнение эллипса.
Большая
полуось а
= 2, малая полуось b
=
 .
.
Координаты
фокусов: F1
(-c;0),
F2
(c;0),
где

Эксцентриситет эллипса равен:

Директрисы эллипса это прямые, уравнения которых

Построим данный эллипс:

Ответ:
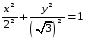 –
каноническое уравнение эллипса;
–
каноническое уравнение эллипса;
большая
полуось а
= 2, малая полуось b
=
 ;
;
эксцентриситет эллипса равен:

директрисы
эллипса:

координаты
фокусов:
 .
.
Задача №9
Найти общее уравнение плоскости, проходящей через точки M1, M2 и M3, и расстояние от точки M0 до этой плоскости. Координаты точек M1, M2, M3 и M0:
M1 (– 1, 2, – 3), M2 (4, – 1, 0), M3 (2, 1, – 2), M0 (1, – 6, – 5).
Решение.
Уравнение плоскости, проходящей через точки М1 (-1,2,-3), М2 (4,-1,0), М3 (2,1,-2), запишется так:

или

Найдем расстояние от точки М0 (1,-6,-5) до плоскости y + z +1 = 0:

Ответ:
уравнение плоскости

Расстояние
от точки М0
до плоскости:
d
=

Задача №10
Найти
канонические и параметрические уравнения
прямой, заданной как пересечение двух
плоскостей. Общие уравнения плоскостей,
объединенные в систему:
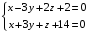
Решение.
В
качестве направляющего вектора прямой
возьмем векторное произведение нормалей
данных плоскостей, т.е. ,
где
,
где
 .
.
Тогда,

 .
.
Возьмем какую-нибудь точку данной прямой. Полагаем z ≠ 0, значения x и y определяем из системы уравнений:
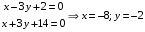
На прямой зафиксировали точку М0 (-8;-2;0).
Уравнения прямой запишутся так:
 – каноническое
уравнение прямой;
– каноническое
уравнение прямой;
 – параметрические
уравнения прямой.
– параметрические
уравнения прямой.
Ответ:
каноническое уравнение прямой –
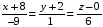 ;
;
параметрические
уравнения прямой –
 .
.
Задача №11
Найти угол между прямой и плоскостью. Если прямая и плоскость не параллельны, то найти точку их пересечения. Канонические уравнения прямых и общие уравнения плоскостей:
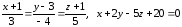 .
.
Решение.
Направляющий
вектор данной прямой:

Нормальный
вектор данной
плоскости:

Синус угла между прямой и плоскостью найдем по формуле:
 Тогда
Тогда

Найдем точку пресечения прямой и плоскости.
Запишем уравнение прямой в параметрическом виде:
 Подставим
выражения для x,
y,
z
в уравнение плоскости:
Подставим
выражения для x,
y,
z
в уравнение плоскости:

Из уравнения прямой получим координаты точки пересечения:

Точка М0 (2; -1; 4) – точка пересечения данных прямой и плоскости.
Ответ:
угол пересечения прямой и плоскости

 ;
;
точка пересечения – М0 (2; -1; 4).

