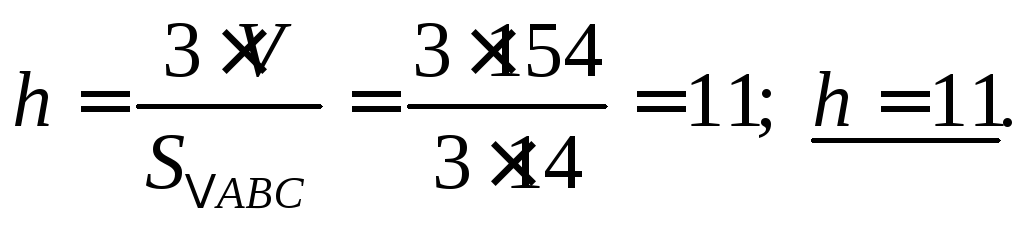Федеральное агентство по образованию

Государственное образовательное учреждение высшего

профессионального образования

«МАТИ» - Российский государственный технологический

университет им. К.Э.Циолковского

Кафедра «Высшая математика»

Практические указания

по векторной алгебре

(варианты курсовых работ)

Составители: Заварзина И. Ф.

Ионова А. С.

Кулакова Р. Д.

Москва 2006

Содержание.

1. Введение.

2. Основные понятия векторной алгебры, примеры решения задач.

3. Теоретические вопросы к защите курсовой работы

4. Варианты курсовых работ.

5. Список литературы.

Введение.

Методические указания по векторной алгебре предназначены для студентов 1 курса всех специальностей дневного и вечернего отделений. Методические указания по векторной алгебре содержат примеры решения некоторых задач векторной алгебры с необходимыми теоретическими обоснованиями этих решений, а также варианты курсовых работ и теоретические вопросы к защите курсовых работ.

1. Основные понятия векторной алгебры; примеры решения задач.

Основные понятия включают в себя: понятие вектора, разложение вектора по другим векторам, модуль вектора, скалярное произведение, векторное произведение и смешанное произведение, а также их приложения для решения задач.

Пример 1. Задание. Разложить вектор по векторам

Прежде чем привести решение задачи напомним понятие линейной зависимости системы векторов.

Рассмотрим систему векторов и составим равенство вида:

–постоянные величины. Если это равенство выполняется только при одновременном равенстве нулю всех ,

, тогда система векторов называется линейно независимой , в противном случае – система векторов линейно зависима, то есть один вектор можно представить в виде линейной комбинации других векторов.

. Разделим левую и правую части равенства на , получим:

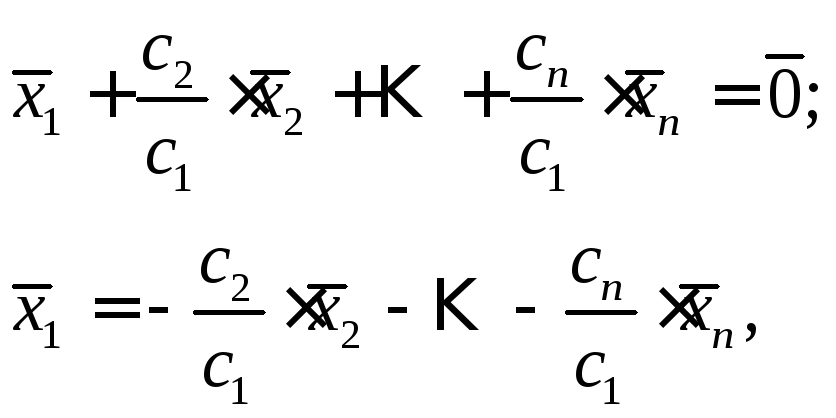
то есть вектор представлен в виде линейной комбинации.

Решение.

Разложить вектор по векторамэто значит представить его в виде линейной комбинации– искомые числа.

Представим линейную комбинацию в координатной форме

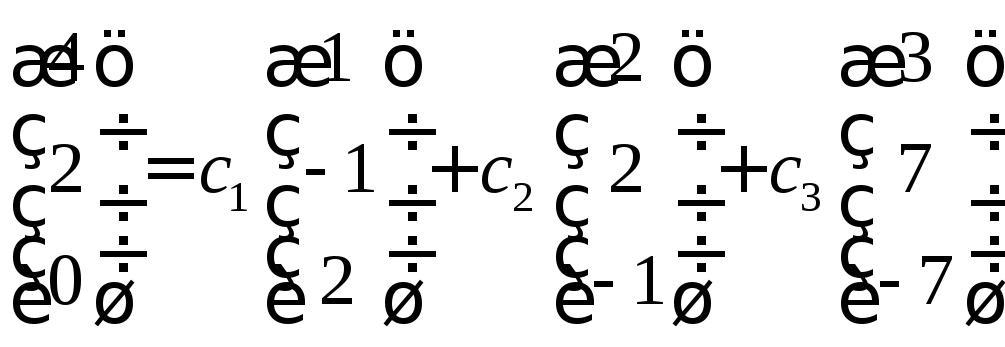
И получим систему линейных уравнений

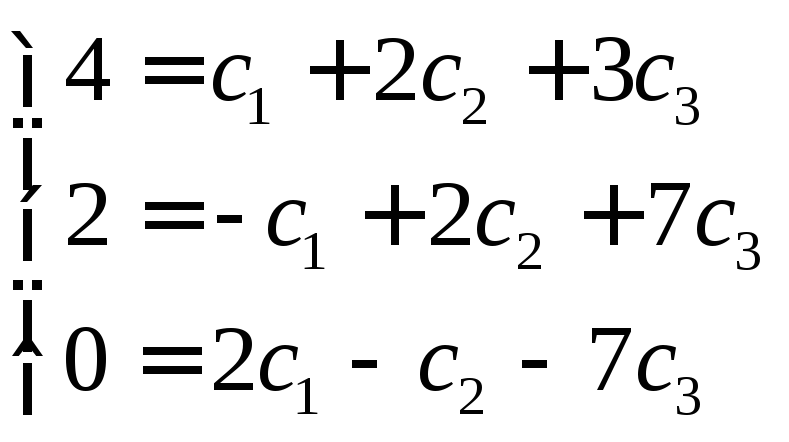
Решение системы имеет вид:

Следовательно:

Пример 2.

Напомним понятие длины вектора (модуля вектора)

Если , то

–называется длиной вектора.

Рассмотрим свойство скалярного произведения: , то есть.

Задание.

Найти длину вектора , если

Решение. Имеем

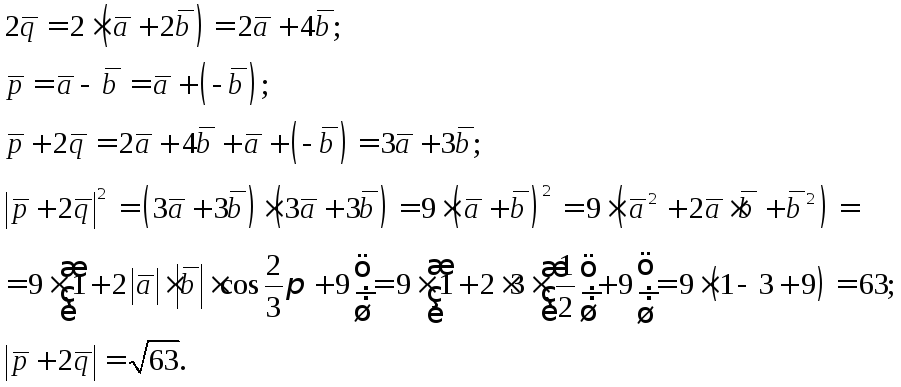
Пример 3.

Напомним определение коллинеарности двух векторов отличных от нуля: два вектораназываются коллинеарными, если, где– некоторый постоянный множитель.

Задание.

Найти вектор , коллинеарный векторуи удовлетворяющий условию: скалярное произведение векторов.

Решение.

Запишем условие коллинеарности двух векторов и полученный векторподставим в условие

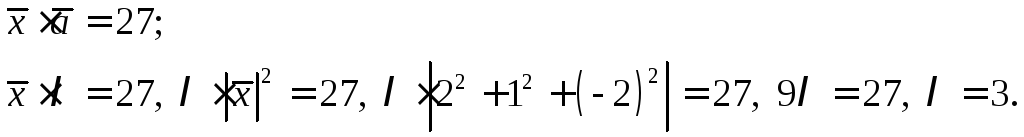
Следовательно .

Пример 4.

Напомним определение скалярного произведения векторов:

.

Задание.

Вычислить проекцию вектора на направление вектора, если

Решение.

Обозначим , тогда

, отсюда

Ответ:

Пример 5.

Пусть . Напомним, что векторное произведение двух векторовиравно: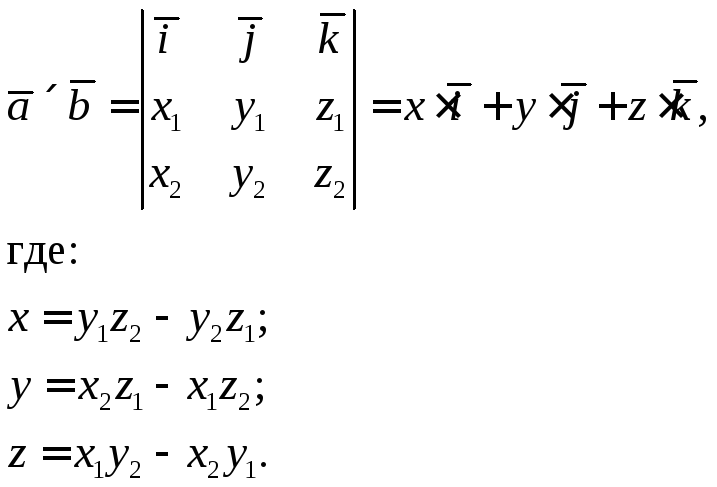

Модуль векторного произведения равен площади параллелограмма, построенного на этих векторах.

Задание.

Найти площадь треугольника

Решение.

Построим параллелограмм на векторах(рис. 1):

рис. 1

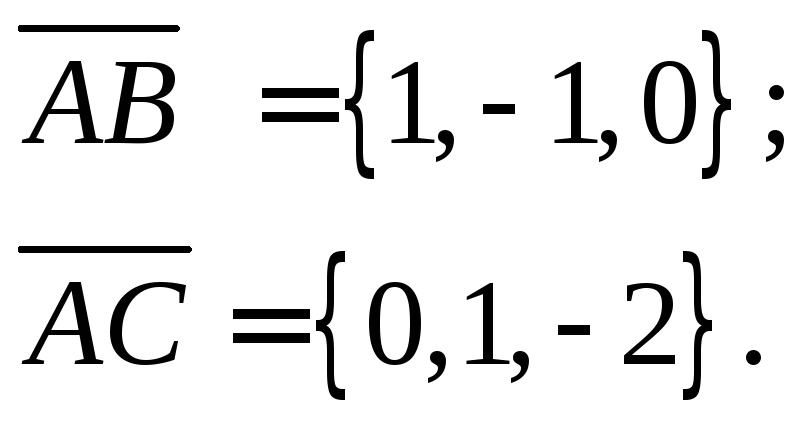
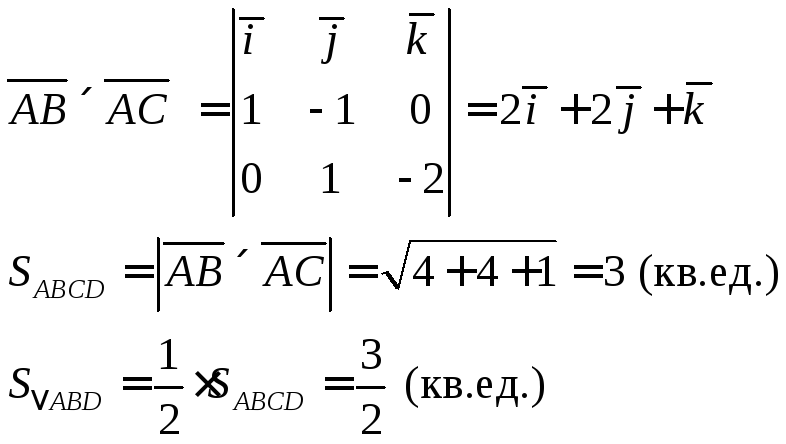
Пример 6.

Задание.

Найти вектор , перпендикулярный векторами образующий с осьютупой угол, если.

Решение.

Если , тогда векторперпендикулярен векторам.

Найдем вектор :

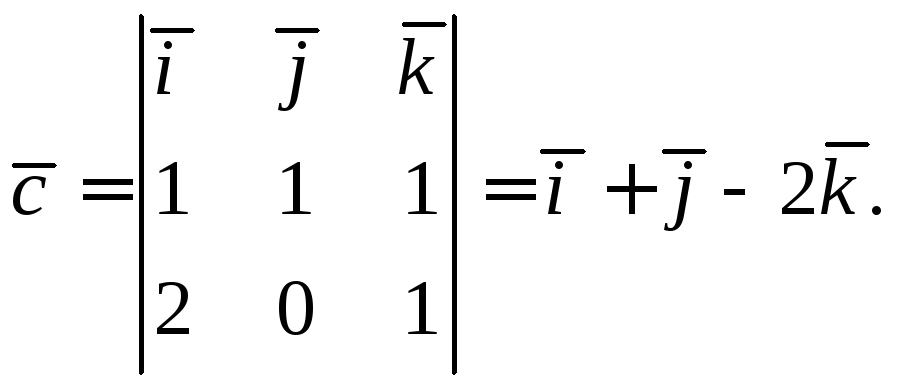
Так как тоже перпендикулярен, следовательно вектораи- коллинеарны. Запишем условие коллинеарности векторов:,

По условию , то есть

Так как вектор образует с осьютупой угол, то его проекция на осьдолжна быть отрицательной.

Отсюда

Пример 7.

Рассмотрим вектор . Векторобразует с осями координат углы, аназываются направляющими косинусами, при этом

Задание.

Найти направляющие косинусы вектора силы , приложенной в точке, и момент этой силы относительно точки.

Решение.

Найдем направляющие косинусы вектора силы:

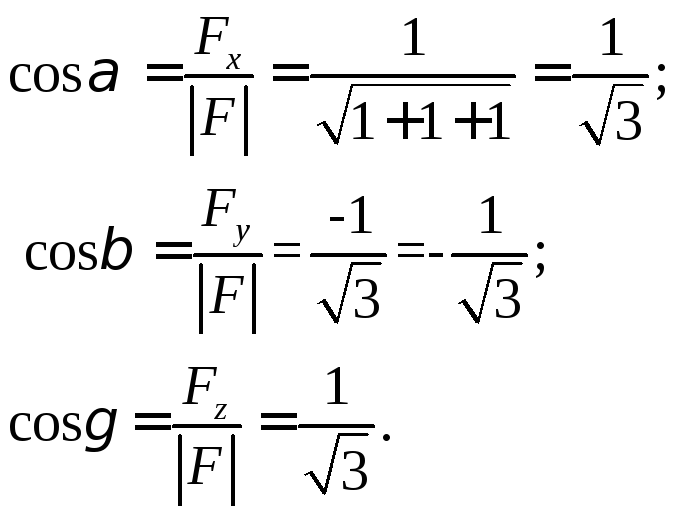
Момент силы определим как векторное произведение вектора на вектор. Имеем

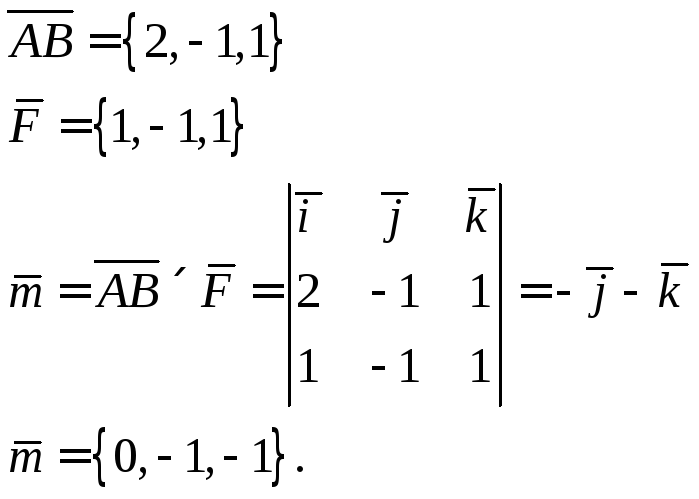
Пример 8.

Напомним формулу смешанного произведения трех векторов

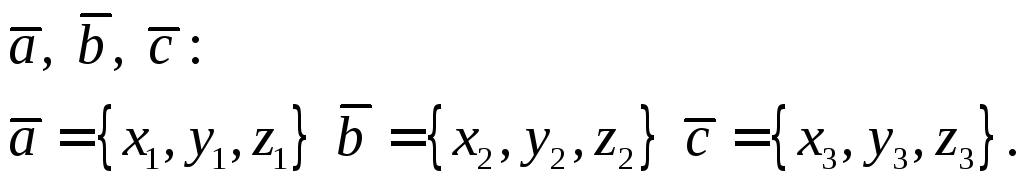
Известно, что модуль смешанного произведения равен объему параллелепипеда, построенного на этих векторах.

Задача.

Найти длину высоты пирамиды, опущенной из вершины (рис. 2), если ее вершины

Решение.

рис. 2

Найдем векторы:

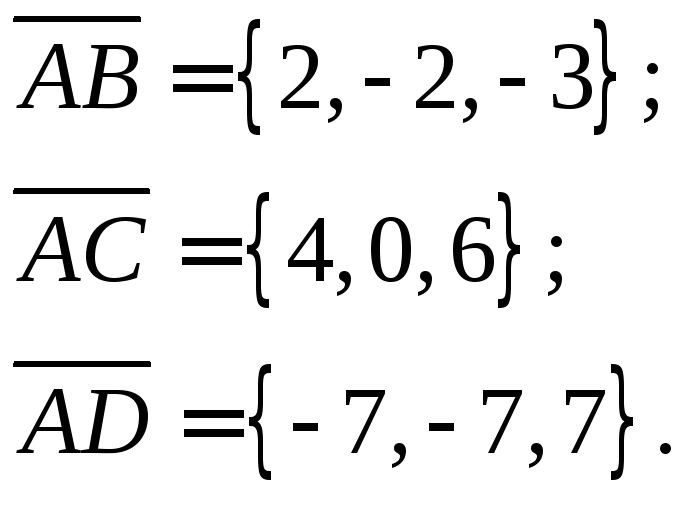
Объем пирамиды, построенной на векторах , равен одной шестой модуля смешанного произведения этих векторов.

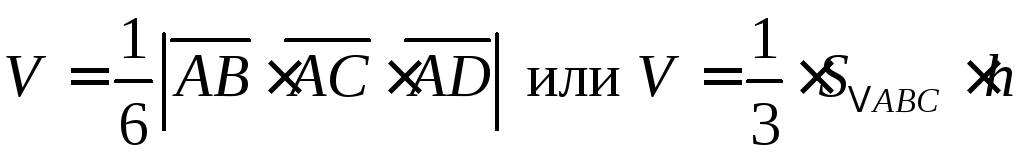, где – высота пирамиды, а площадь прямоугольника, построенного на векторахравна одной второй векторного произведения.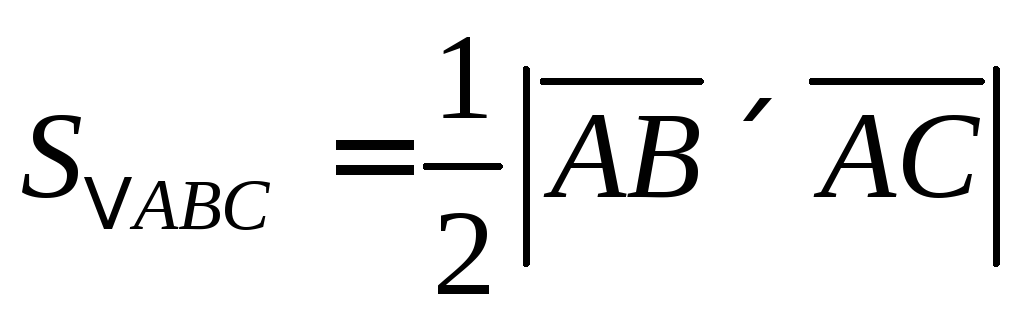

Вычислим смешанное произведение векторов

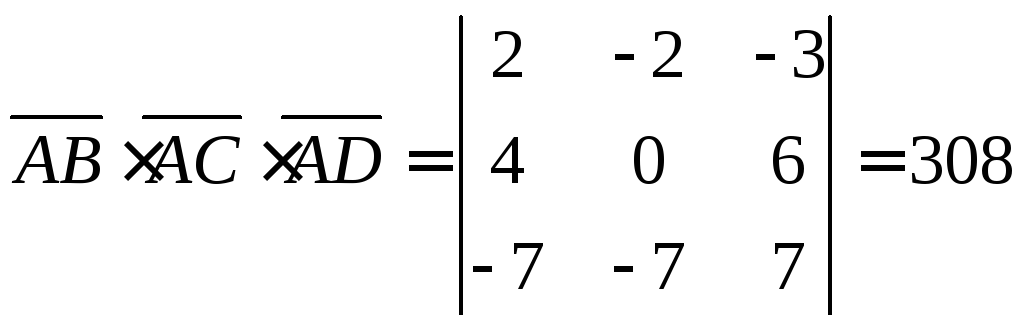
Отсюда пирамиды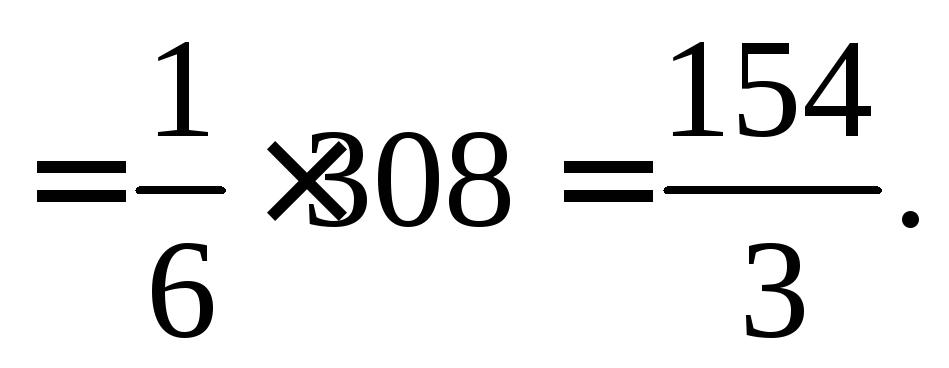

Вычислим векторное произведение векторов:

Найдем высоту пирамиды: