Лекция №14 Свойства предельной функции и сумма функционального ряда в случае равномерной сходимости

Теорема 1. Если

Доказательство. Будем исходить из следующей оценки:

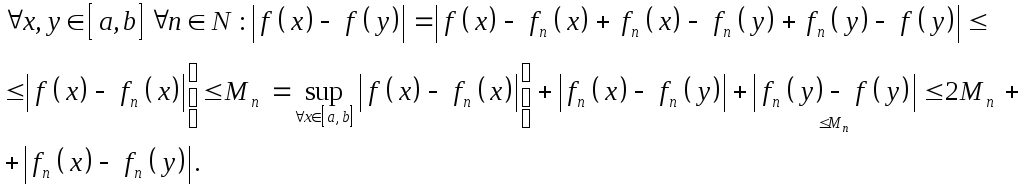
Итак,

Зафиксируем функция

равномерно непрерывна на [a, b]

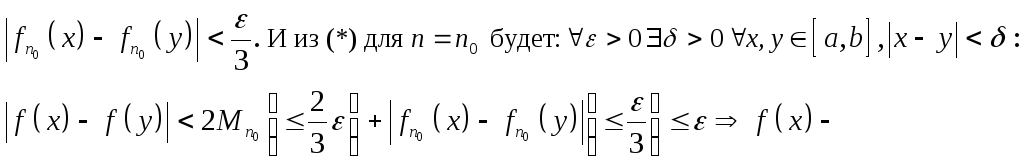
равномерно непрерывна на [a, b].

Доказано.

Теорема 1. Если непрерывна, функциональный рядсходится кто

Доказательство. Если частичные суммы, тотакже непрерывна и равномерно сходится к

Утверждение теоремы 1 вытекает из теоремы 1.

Доказано.

Теорема 2. Если

Доказательство. Будем пользоваться следующим критерием интегрируемости функции по Риману (критерий Римана):

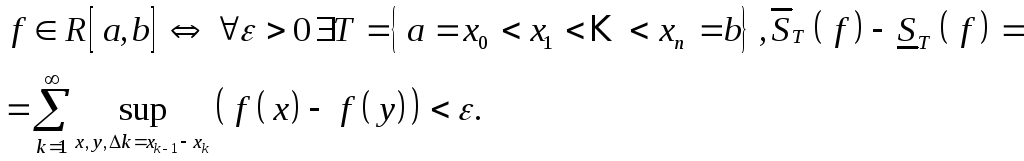
Пустьпроизвольное разбиение, тогда:

Итак,

Опять а из

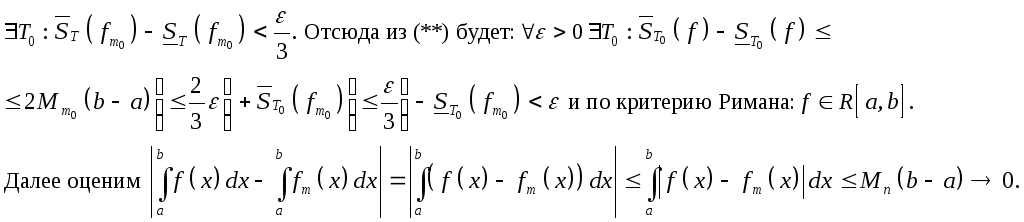
Это и означает справедливость второй части теоремы 2.

Доказано.

Теорема 2. Если , и функциональный рядсходится кто

Доказательство. Если По теореме 2(по теореме 2) =

Доказано.

Теорема 3. Если

1. 

2. 

3. 

то также равномерно сходится к

.

Доказательство. Будем пользоваться следующими критерием:

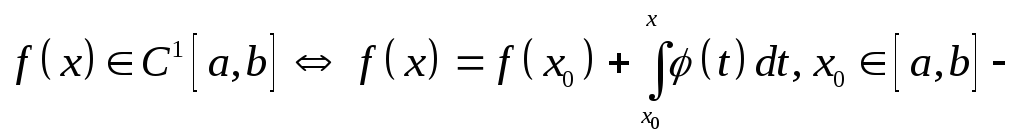произвольное, а Далее пользуясь критерием Коши, покажем равномерную сходимость последовательности

равномерно по Далее:

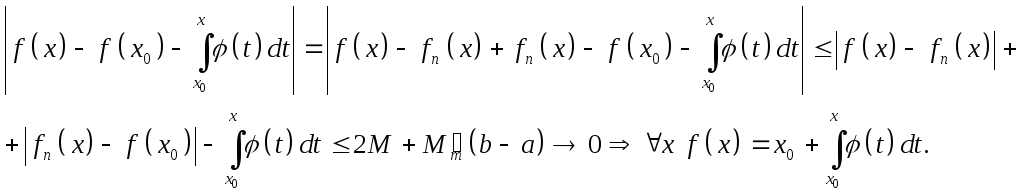
Доказано.

Пример 1. Исследовать сходимость функционального ряда

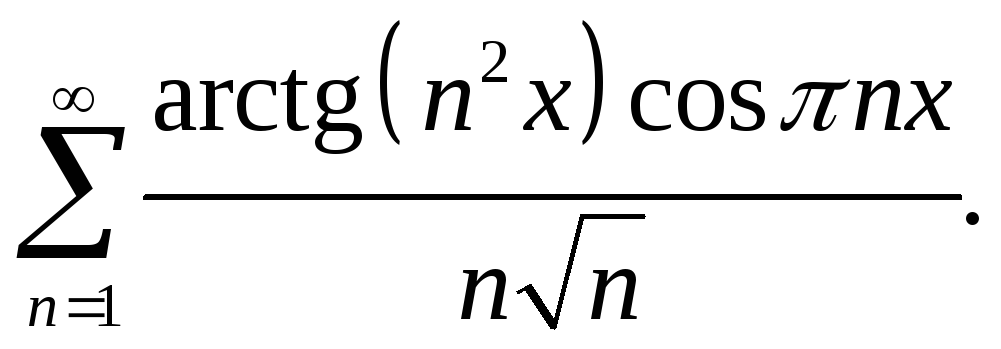
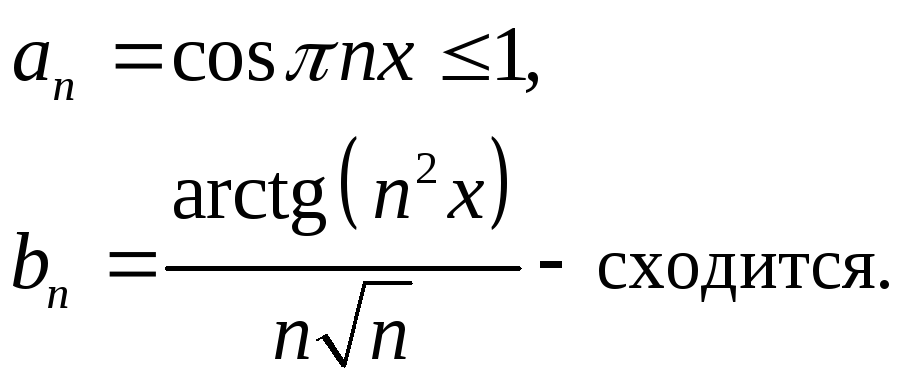
Пример 2. Исследовать сходимость функционального ряда

Пример 3. Исследовать сходимость функционального ряда

Теорема 3. Если

1. 

2. 

3. 

Доказательство. Если то

1. 

2. 

3. 

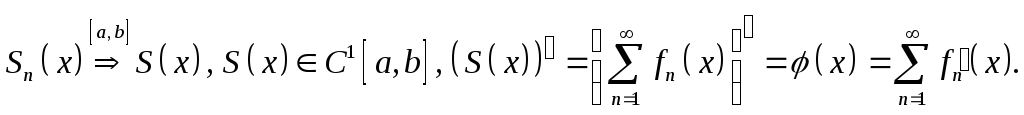
Доказано.

Лекция №15 Пространства и сходимость в них

1. Случай .

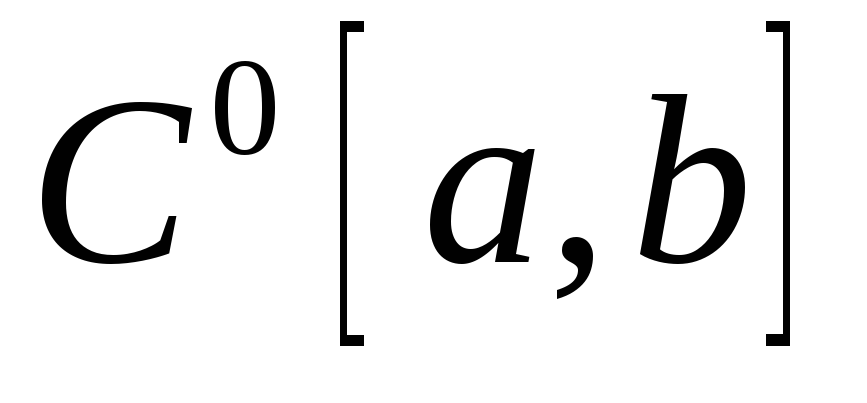В этом случае - линейное пространство бесконечной размерности, в котором можно ввести норму для которой выполнены свойства:

1. 

2. 

3. 

Линейное пространство с нормой называется нормированным пространством.

Норма позволяет определить сходимость [a, b]:

Последовательность функции называется фундаментальной, если Нормированное пространство, в котором всякая фундаментальная последовательность является сходящейся, называетсяполным, или банаховым пространством (по имени С. Банаха).

Отметим, что всякая сходящаяся последовательность является фундаментальной, т.е. в полном пространстве сходимость эквивалентна фундаментальности, или в полном пространстве выполнен критерий Коши.

Покажем, что нормированное пространство является полным. Для этого рассмотрим сходимость в нём:

Итак, сходимость по норме пространства эквивалентна равномерной сходимости.

Известно, что для равномерной сходимости выполнен критерий Коши. Это и означает, что пространство - полное.

Пример. В пространстве введём норму. Полученное пространство будет нормированным, но не полным, например, в нём будет фундаментальная следующая система функций.

Можно указать фундаментальную последовательность , но не сходящуюся к непрерывной функции. Это нормированное пространство можно пополнить, и элементами этого пополнения будут функции, интегрируемые на [0, 1] по Лебегу.

2. Пространство

Это линейное пространство, в котором можно ввести норму

Охарактеризуем сходимость в этом пространстве:

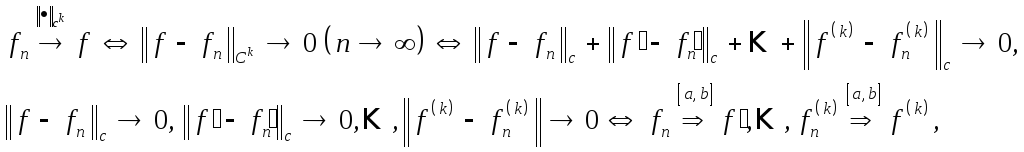
т.е. сходимость по норме пространства эквивалентна равномерной сходимости самой последовательности и последовательности её производных порядкаk включительно.

Отметим, что пространство также является полным.

Пространство с нормойне будет полным и его пополнение – это так называемоепространство Соболева .