ЛАБОРАТОРНАЯ РАБОТА 1-1.

ИССЛЕДОВАНИЕ СВОБОДНЫХ КОЛЕБАНИЙ

ПРУЖИННОГО И МАТЕМАТИЧЕСКОГО МАЯТНИКОВ.

1. ЦЕЛЬ РАБОТЫ: исследование свободных колебаний пружинного и математического маятников.

2. ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: математический и пружинный маятники, секундомер, грузы, масштабная линейка.

3. МЕТОД ИЗМЕРЕНИЙ: прямые измерения числа колебаний за определенный промежуток времени, а также измерение амплитуды колебания позволяют определить основные характеристики свободных колебаний.

4. ВВЕДЕНИЕ

В данной работе исследуются линейные свободные колебания, описываемые линейными дифференциальными уравнениями вида:

ä + ₀² = 0 (1.1.1)

ä + á +₀² = 0 (1.1.2)

где  - осциллирующая (колеблющаяся) величина;

₀ – собственная циклическая частота колебаний системы;

r – обобщенный коэффициент сопротивления;

m – масса колеблющейся материальной точки.

Физическая система, в которой закон движения подчиняется уравнению (1.1.1), называется гармоническим осциллятором. К нему, в частности, относятся пружинный и математический маятники. Гармонические колебания системы реализуются лишь тогда, когда в них действуют силы, стремящиеся вернуть систему в ее первоначальное положение равновесия и пропорциональные отклонению системы от положения равновесия. Такие силы иногда называются восстанавливающими.

(1.1.3)

Примером таких сил служат силы упругости. Свободные колебания – это колебания, которые происходят под действием восстанавливающей силы.

В реальных осцилляторах происходит рассеяние (диссипация) колебательной энергии и свободные колебания со временем затухают. Уравнение (1.1.2) учитывает процесс диссипации энергии. В нем имеется слагаемое, которое характеризует силу сопротивления движению F_тр. Эта сила при небольших скоростях движения пропорциональна скорости изменения осциллирующей величины

F_тр = - rá (1.1.4)

Решением уравнения (1.1.1) является функция

(1.1.5)

где _max – амплитуда колеблющейся величины;

₀ – начальная фаза колебания;

t – время.

Периоды гармонических колебаний пружинного и математического маятников соответственно равны

(1.1.6)

(1.1.7)

где l – длина математического маятника.

Решение уравнений (1.1.2) при n  k (n = , k = m₀²) имеет вид:

 = A₀e^-tn cos (_rt+₀) (1.1.8)

где A₀ – начальное отклонение системы от положения равновесия

(начальная амплитуда колебаний);

_r – частота затухающих колебаний; она равна

_r = (1.1.9)

С увеличением трения коэффициент n увеличивается, и при n  ₀ частота оказывается мнимой, колебания прекращаются и движение становится апериодичным.

Энергия колебания, равная максимальным значениям потенциальной или кинетическойэнергии, для затухающих колебаний изменяется по закону

E(t) = E₀e^-2tn (1.1.10)

где E₀ – есть начальная энергия колебаний.

Энергия осциллятора не сохраняется, она расходуется на работу против диссипативных сил и превращается во внутреннюю энергию. Скорость рассеяния энергии, т.е. мощность потерь P_n, равна

или P_n = 2nE (1.1.11)

Характеристикой качества колебательной системы, ее способностью сохранять запасенную энергию служит добротность Q^*, определяемая как отношение запасенной энергии к потерям за время

t =

Q^* = (1.1.12)

Таким образом, Q^* равна числу колебаний за время t = /n. За это время амплитуда уменьшается в 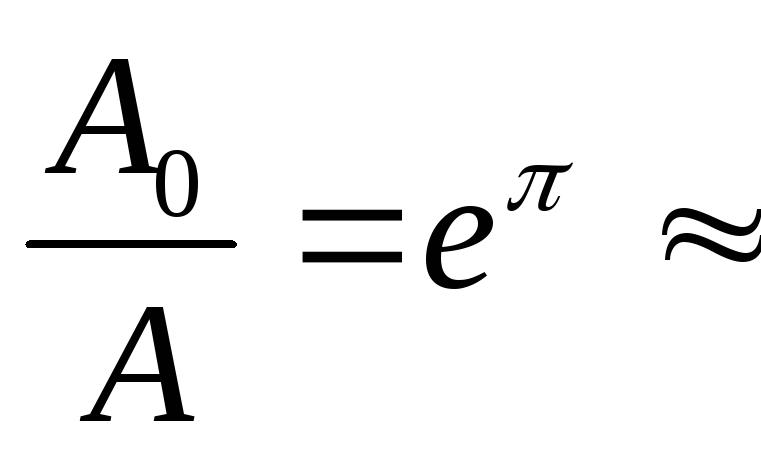23 раза, а энергия в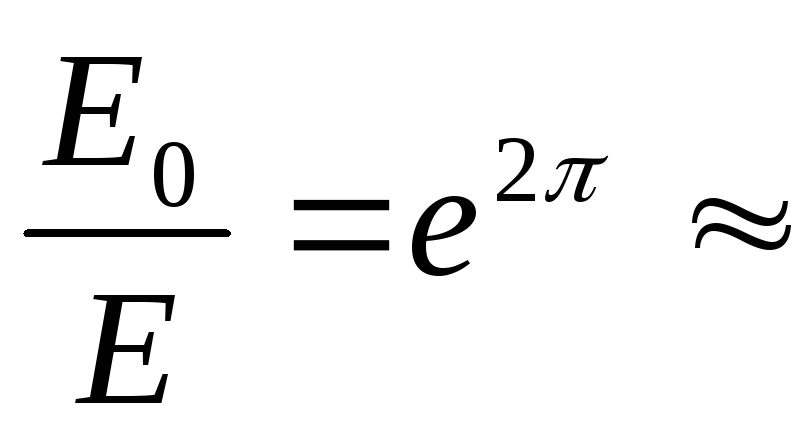535 раз. Коэффициентn носит название коэффициента затухания колебаний. Затухание колебаний принято характеризовать логарифмическим декрементом затухания :

 = ln (1.1.13)

5. Изучение колебаний пружинного маятника.

5.1.ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: пружинный маятник, вертикальная стойка с масштабной линейкой, грузы, секундомер.

5.2.МЕТОД ИЗМЕРЕНИЙ.

Для определения основных характеристик свободных или затухающих колебаний пружинного маятника необходимо найти его коэффициент упругости, период гармонических колебаний, начальную амплитуду (для затухающих колебаний).

5.3. Проведение эксперимента и обработка опытных данных по изучению гармонических колебаний.

5.3.1. Для определения коэффициента упругости (жесткости) пружины подвесить к пружине груз массой m и определить ее удлинение l. Этот опыт осуществить для грузов массами m₁, m₂, m₃.

5.3.2. Вычислить коэффициент пружины k₁ в каждом опыте по формулам:

k₁ = ; k₂ = ; k₃ = (1.1.14)

Найти среднее значение величины k:

k = (1.1.15)

5.3.3. Определить расчетные значения периода гармонических колебаний маятника T_i для грузов массой m₁, m₂, m₃ по формуле (1.1.6).

5.3.4. Приподнять груз пружины от положения его равновесия и отпустить. Пружинный маятник придет в колебательное движение. Измерить время t его полных колебаний N(N30) и найти период T_i по формуле:

T_i = (1.1.16)

Этот опыт нужно проделать с тремя различными грузами и для каждого опыта вычислить коэффициент жёсткости по формуле

(1.1.17)

где m_i – масса груза при i = 1, 2, 3.

Затем рассчитать среднее значение коэффициента жесткости пружины k по формуле (1.1.15).

5.3.5. Вычислить энергию колебаний пружинного мятника по формуле:

(1.1.18)

где A_0i – наибольшее смещение груза относительно положения его равновесия.

Результаты измерений и вычислений занести в таблицу 1.

Таблица 1

№ опыта	m кг	li м	ki н/м	k= н/м	t c	N	Ti= c	ki= н/м	Ti=2 c	A0i м	Ei= Дж
1	m1
2	m2
3	m3

5.3.6. Определить погрешности однократного косвенного изменения периода колебаний T. Для этого нужно найти суммарную относительную погрешность измерений по формуле (1.1.19)

_= 1/2 m + 1/2 k_ (1.1.19)

где m - относительная погрешность массы груза; m = ;

m_ - суммарная относительная погрешность измерения;

k – коэффициент жесткости пружины.

k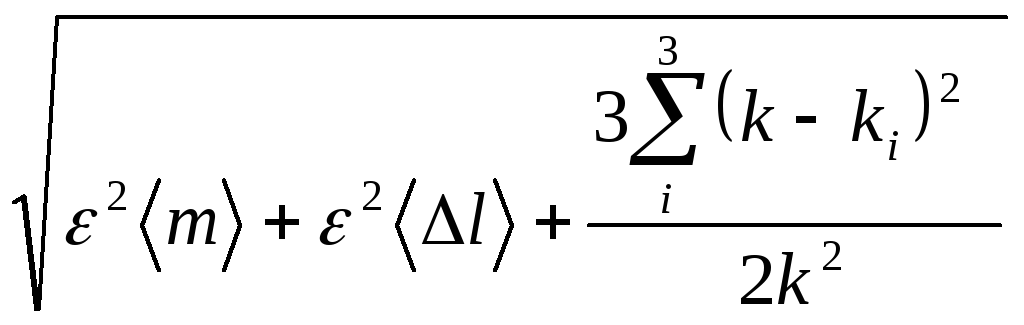_ = (1.1.20)

Абсолютная погрешность однократного измерения T равна

 = T T_

Тогда выражение для истинного значения периода колебаний T_u примет вид

T_u = T   (1.1.21)

5.4. Проведение эксперимента и обработка опытных данных по изучению свободных затухающих колебаний пружинного маятника.

5.4.1. Подвесить к пружине груз массой m = 0,6 кг, отклонив его от положения равновесия на величину A₀ = 8 см. Осторожно отпустить груз, и тогда система придет в колебательное движение.

5.4.2. Измерить время t, за которое начальная амплитуда колебания A₀ уменьшится в 10 раз и составит A_t = 0,1A₀, и подсчитать число полных колебаний системы N за это же время.

5.4.3. Вычислить логарифмический декремент затухания. Для этого нужно найти коэффициент затухания n.

B = =e^nt (1.1.22)

Прологарифмируем полученную величину

ln B = ln e^nt=nt (1.1.23)

Откуда

n = (1.1.24)

Затем по формуле (1.16) нужно найти период собственных колебаний T₀. Период затухающих колебаний вычислить по формуле

T = (1.1.24)

Окончательная формула для вычисления логарифмического декремента пружинного маятника будет:

 =

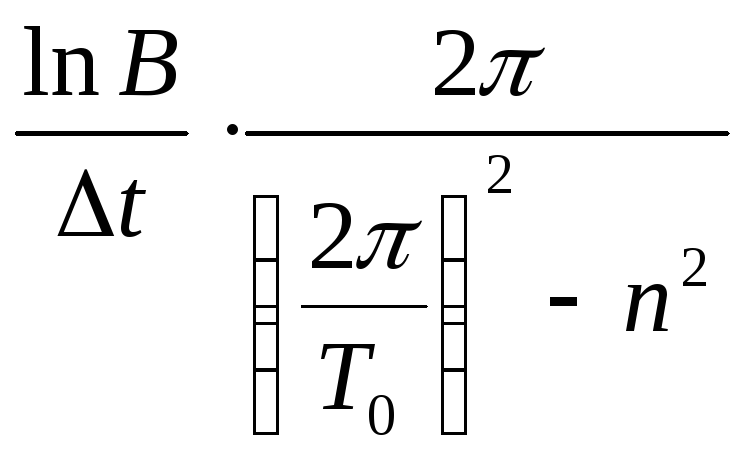
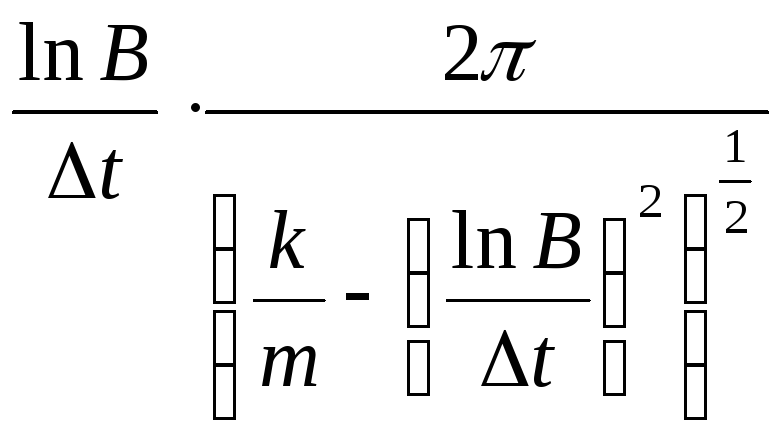=(1.1.25)

5.4.4. Найти добротность маятника

Q^ = (1.1.26)

5.4.5. Рассчитать обобщенный коэффициент трения r.

r = 2mn. (1.1.27)

Результаты измерений и вычислений занести в таблицу 2.

5.4.5. Определить погрешность косвенного измерения коэффициента затухания n по данным таблицы 2:

n = (1.1.28)