Физика ответы

vk.com/club152685050 | vk.com/id446425943

Вопрос 13

Полем сил называют область пространства, в каждой точке которого на помещенную туда частицу действует сила, закономерно меняющаяся от точки к точке (поле силы тяжести Земли). Если сила в каждой точке силового поля не зависит от времени, то такое поле называют стационарным. Ясно, что силовое поле, стационарное в одной системе отсчета, в другой системе может оказаться и нестационарным. В стационарном силовом поле сила зависит только от положения частицы.

Стационарное силовое поле, в котором работа силы поля на пути между двумя любыми точками не зависит от траектории, а зависит только от положения этих точек, называется потенциальным, а сами силы – консервативными (F тяж, F упр). Если это условие не выполняется, то силовое поле не является потенциальным, а силы поля называют неконсервативными (F трения).

Свойства консервативных сил:

1) работа, производимая консервативной силой, определяется только начальным и конечным положением точки её приложения и не зависит от выбора траектории, по которой перемещается тело.

2) работа консервативных сил по произвольному замкнутому контуру равна 0;

3) — ротор консервативных сил равен 0;

4) — консервативная сила является градиентом некой скалярной функции, называемой силовой. Эта функция равна потенциальной энергии, взятой с обратным знаком. Соотношение:

Таким образом, потенциальная сила всегда направлена в сторону уменьшения потенциальной энергии.

Вопрос 14

Потенциальная энергия частицы в поле.

В стационарном поле работа консервативных сил зависит только от начального и конечного положения частицы. Представим такое поле, где частица перемещается от разных точек Pi в точку О. Работа сил не зависит от пути, поэтому зависит только от положения точки Р.  Работа будет некоторой ф-ей радиусвектора r точки Р. Эта ф-я будет обозначатся как U(r):

Найдем работу при перемещении точки из 1 в 2. Т.к. она не зависит от пути, то выберем путь через точку О, тогда:

или

Выражение справа (U1-U2) есть убыль потенциальной энергии или разность значение Еп в начальной и конечной точках пути. Таким образом, работа сил на пути 1-2 равна убыли потенциальной энергии.

Связь между потенциальной энергией и силой.

Каждой точке потенциального поля соответствует, с одной стороны, некоторое значение вектора силы F, действующей на тело, и, с другой стороны, некоторое значение потенциальной энергии Eп.

Для установления связи вычислим элементарную работу dA, совершаемую силами поля при малом перемещении dr тела, происходящем вдоль произвольно выбранного направления в пространстве, которое обозначим буквой r. Эта работа равна

dA=Fdr= - dEп

где F- проекция силы на направление r. Поскольку в данном случае работа совершается за счет запаса потенциальной энергии Eп, она равна разности потенциальной энергии –dЕп на отрезке оси. А отсюда получаем:

F= -dEп/dr;

Если разложить F по осям, то:

11

vk.com/club152685050 | vk.com/id446425943

В векторном виде сила равна (grad – градиент):

Градиент – вектор, показывающий направление наибыстрейшего увеличения ф-и. “-“ показывает то, что вектор F направлен в сторону наибыстрейшего уменьшения Eп.

 Консервативная сила равна отрицательному градиенту Eп:

Билет 15

Полная механическая энергия частицы – энергия механического движения и взаимодействия, равная сумме кинетической и потенциальной энергий: E = Ek + Ep.

Док-во:

Приращение Ек или Т равно элементарно работе результирующей Fрез всех сил. В стационарном поле это консервативная сила этого поля Fконс и иные силы Fстор.  Fрез = Fконс + Fстор. Робота этих сил идет на приращение кинетической энергии частицы:

Т.к. работа равна убыли потенциальной энергии Аконс = - U, то подставив это в выражение, после преобразований получим:

Отсюда видно, что работа сторонних сил идет на приращение величины T+U, что и есть полная механическая энергия.

Закон сохранения.

Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только посредством сил тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком:

По теореме о кинетической энергии эта работа равна изменению кинетической энергии тел:

Следовательно:

Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой посредством сил тяготения и сил упругости, остается неизменной.

Билет 16

Кинетическая энергия механической системы - это энергия механического движения рассматриваемой системы. Обозначается как Ек или Т.

Теорема о кинетической энергии системы — одна из общих теорем динамики, является следствием законов Ньютона. Связывает кинетическую энергию механической системы с работой сил, действующих на тела, составляющие систему. В качестве системы, о которой идёт речь, может выступать любая механическая система, состоящая из любых тел.

Кинетической энергией системы называют сумму кинетических энергий всех тел, входящих в систему. Для определённой таким образом величины справедливо утверждение:

Изменение кинетической энергии системы равно работе всех внутренних и внешних сил, действующих на тела системы.

Док-во теоремы:

12

vk.com/club152685050 | vk.com/id446425943

Рассмотрим систему материальных точек с массами mi, скоростями vi и кинетическими энергиями Ti=1/2(mivi2). Для малого изменения кинетической энергии (дифференциала), происходящего в течение некоторого малого промежутка времени dt будет выполняться:

Учитывая, что dvi/dt представляет собой ускорение i-ой точки - ai, а dvi/dt— перемещение si той же точки за время dt, полученное выражение можно записать в виде:

Используя второй закон Ньютона и обозначая равнодействующую всех сил, действующих на точку, как Fi получаем:

, Fidsi есть работа А 

Суммирование всех уравнений такого вида, записанных для каждой из материальных точек, приводит к формуле для изменения полной кинетической энергии системы:

Данное равенство выражает утверждение теоремы об изменении кинетической энергии системы в дифференциальном виде.

Проинтегрировав обе части полученного равенства по произвольно взятому пром ежутку времени получим выражение теоремы об изменении кинетической энергии в интегральной форме:

где T2 и Т1 — значения кинетической энергии системы в моменты времени t2 и t1 cсоответственно.

Необходимо подчеркнуть, что здесь, в отличие от случаев теоремы об изменении количества движения системы и теоремы о движении центра масс системы, учитывается действие не только внешних, но внутренних сил.

Собственная потенциальная энергия системы - механическая энергия системы тел, которая определяется характером сил взаимодействия между телами этой системы и их взаимным расположением.

Рассмотрим систему, между частицами которой действуют лишь центральные силы. Центральные силы – силы, зависящие от расстояния между частицами и направленные по прямой, проходящий через эти частицы (граф. инт. в Вопросе 11).

Покажем, что независимо от системы отсчета работа внутренних сил при переходе системы частиц из одного положения в другое может быть представлена как убыль некоторой ф-и, которая зависит только от расположения частиц в системе , т.е.

от конфигурации. Эта ф-я и является собственной потенциальной энергией системы.

Сначала возьмем систему из двух частиц. Работа в К-системе отсчета за время dt будет выглядеть как:

Согласно Третьему закону Ньютона F2=-F1, тогда:

Величина в скобках представляет собой перемещение частицы 1 относительно частицы 2. Вспомним принцип относительности Галилея (вопрос 8), тогда частица 1 перемещается в K’ системе, которая жестко связана с частицей два и перемещается вместе с ней относительно исходной системы K.  dr1 = dr2+dr’1, dr1-dr2=dr’1 и:

 Алгебраическая сумма элементарных работ пары сил взаимодействия в произвольной К-системе оказывается равной элементарной работе, которую совершает сила, действующая на одну частицу, в к системе отсчета, где другая

покоится.  А1,2 не зависит от выбранной системы отсчета. F1 действующая на частицу 1 со стороны частицы 2 центральная, а значит консервативная. Поэтому является убылью потенциальной энергии 1 в поле частицы 2 или как:

Рассмотрим систему из 3-ех частиц. По тому же принципу:

т.к ,то

, где Uсоб – собственная потенциальная энергия системы. Uсоб будет завесить от конфигурации системы.

Данное утверждение абсолютно для любого числа частиц, поэтому каждой конфигурации системы частиц присуще свое значение Епсобст и работа всех внутренних центральных сил при изменении конфигурации есть убыль Епсобст:

13

vk.com/club152685050 | vk.com/id446425943

А теперь фокус-покус блять. Uсобст не является сумме собственных потенциальных энергий ее частей т.к.

Преобразуем представив каждое слагаемое в виде (Uik = Uik+Uki)/2 т.к Uik=Uki, тогда:

,а после группировки по индексам

, что есть ничто иное как

,а в общем виде

Классификация сил. По характеру взаимодействия:

Массовые (объёмные) силы обусловлены взаимодействием материальных тел на расстоянии, они приложены к каждой точке тела (распределены по всему его объёму). К массовым силам относятся силы гравитационного и электромагнитного взаимодействия. Обычно из чисто формальных соображений к ним добавляют силы инерции (для сил инерции невозможно указать конкретный материальный источник).

Поверхностные силы приложены к участкам поверхности и являются результатом взаимодействия материальных тел при непосредственном контакте. В зависимости от соотношения площади приложения нагрузки и общей площади поверхности рассматриваемого тела, поверхностные силы подразделяются на сосредоточенные и распределённые. К первым относятся нагрузки, площадь приложения которых несоизмеримо меньше площади поверхности тела. Таковыми являются, например, сила нормального давления P и сила трения T между колесом тележки и подкрановой балки, а также силы взаимодействия балки с опорами.

Билет 17

Преобразования Лоренца − преобразования координат и времени какого-либо события при переходе от одной инерциальной системы отсчёта к другой. (Инерциальная система отсчёта – система отсчёта, движущаяся прямолинейно с постоянной скоростью v).

Если инерциальная система отсчёта K' движется относительно инерциальной системы отсчёта K с пос тоянной скоростью v вдоль оси x, то преобразования Лоренца имеют вид

y = y', z =

z',

c - скорость света в вакууме, β = v/c. Формулы, выражающие x', y', z', t' через x, y, z, t получаются из соотношения (1) заменой v на -v.

Рис. Система координат K' движется относительно неподвижной системы координат K со скоростью v вдоль оси x.

При v < c преобразования Лоренца переходят в преобразования Галилея: x = x' + vt, y = y', z = z', t = t'.

Формулы преобразования скорости:

14

vk.com/club152685050 | vk.com/id446425943

Сложение скоростей

Тело движется в системе K’, которая сама движется относительно системы K. Скорость движения этого теля относительно неподвижной системы отсчёта K равна веЛакторной сумме скорости этого тела относительно подвижной системы отсчета K’ и скорости той точки подвижной системы отсчёта, в которой в данный момент времени находится тело (относительно неподвижной системы).

Длина стержня в системе К:

Из преобразований Лоренца:

,т.о.:

Линейные размеры тела наибольшие в той инерциальной системе отсчёта, относительно которой тело покоится.

Длительность событий в разных системах отсчёта.

Пусть в некоторой точке (с координатой х), покоящейся относительно системы К, происходит событие, длительность которого ,где индексы 1 и 2 соответствуют началу и концу события. Длительность этого же события в системе К’: ,причём началу и концу события, согласно преобразованиям Лоренца, соответствуют:

Представляя второе в первое получим:

Отсюда видно, что , т.е. длительность события, происходящего в некоторой точке, наименьшая в той инерциальной системе отсчёта, относительно которой эта точка неподвижна. Следовательно, часы, движущиеся относительно инерциальной системы отсчёта, идут медленнее покоящихся часов, т.е. ход часов замедляется в системе отсчёта,

относительно которой часы движутся. Из . следует, что замедление хода часов становиться заметным лишь при скоростях, близких к скорости света в вакууме.

Билет 18

v – скорость частицы, а m – Ньютоновская масса. В случае малых скоростей эти соотношения дают обычный результат

. Второй закон Ньютона – основное уравнение движения в классической механике. [V(t)= V0+at]

В опытах с телами, двигающимися быстрее скорости света этот закон не действует, он заменяется на

- уравнение в релятивистской механике.

Кинетическая энергия релятивистской частицы

Правила кинетической энергии, которые действовали в ньютоновской механике, верны также и для релятивистской частицы. Необходимо только видоизменить формулу кинетической энергии частицы и получить релятивистское выражение для кинетической энергии. Воспользуемся с этой целью формулой релятивистской массы Преобразовывая получаем:

Это и есть формула релятивистской кинетической энергии.

Билет 19

Релятивистское выражение для импульса. Найдем такое выражение для импульса, чтобы закон сохранения импульса был неизменным к преобразованиям Лоренца при любых скоростях (как мы уже говорили, уравнения Ньютона не неизменны к преобразованиям Лоренца и закон сохранения импульса в k выполняется, а в k' – нет). Ньютоновское выражение для импульса

15

vk.com/club152685050 | vk.com/id446425943

или	.
В выражении
m – постоянная величина	– масса частицы в системе k (собственная масса частицы), неизменная величина; dt –

интервал времени по часам неподвижного наблюдателя.

Если заменить dt на – собственное время частицы, тоже неизменную величину, то получим неизменное выражение для импульса . Преобразуем это выражение с учетом того, что:

или

Это и есть релятивистское выражение для импульса.

Следует, что никакое тело не может двигаться со скоростью большей или даже равной скорости света (при υ→c знаменатель стремится к нулю, тогда p→∞ , что невозможно в силу закона сохранения импульса).

Масса покоя.

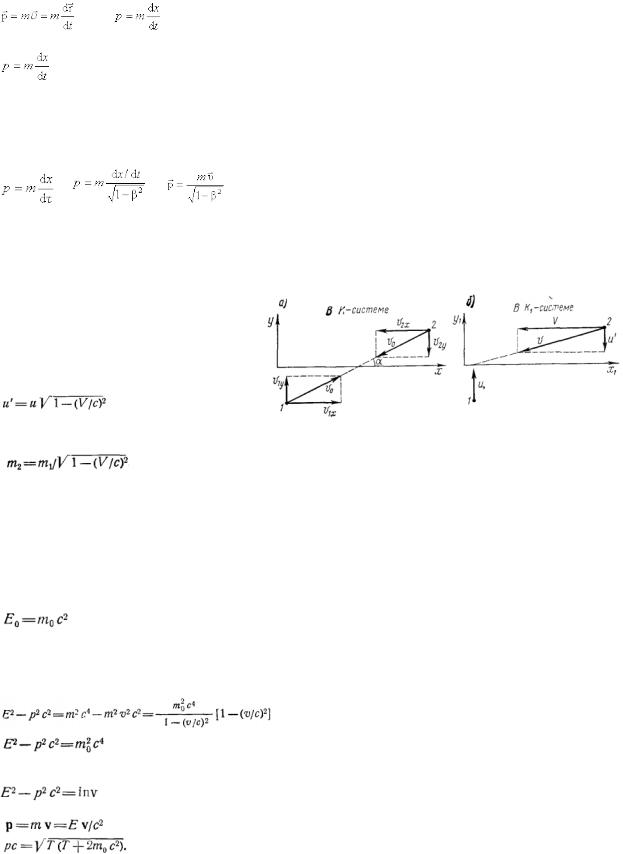
Представим, что есть две частицы с равной массой. Частица 1 движется в СО К1, а частица 2 в системе СО К2 только по осям OY. Сами системы движутся друг на друга с равной по модулю скоростью V. Рассмотрим картину столкновения частиц в системе К1. Согласно преобразованиям Лоренца, скорость частицы 2 по оси OY будет:

Выражения импульсов у-составляющих в системе

К1 для обоих частиц будет выглядеть как m1u и m2u’. Скорости частиц различаются и очевидно, что и закон сохранения импульса сохраняться не будет т.к. массы одинаковы. Потребуем, чтобы закон сохранения импульса выполнялся, тогда:

При a0 u и m1 представляет собой массу покоящейся частицы; ее и обозначают m0, то есть массой покоя. Скорость V в этом случая будет скоростью 2-ой частицы относительно первой, поэтому:

, m – релятивистская масса.

Закон взаимосвязи массы и энергии.

 это закон Е-полная энергия без учета потенциальной.

В другом виде: , т.к.

Тогда E0 будет энергией покоя или собственной энергией:

Связь между энергией и импульсом частицы.

Импульс и энергия различны в разных системах отсчета, однако есть некая инвариантная комбинация (неизменная). Эта комбинация есть E2-p2c2.

Док-во:

Воспользуемся формулами E=mc2 и p=mv, тогда:

, после сокращения

Тот факт, что скорость сократилась в правой части, говорит о том, что величина E2-p2c2 не зависит от скорости частицы, а, следовательно, и от системы отсчета.

Как следствие:

Вопрос 20

Колебательными называют движения, которые в точности или приблизительно повторяются через одинаковые промежутки времени.

16

vk.com/club152685050 | vk.com/id446425943

X(t)=Acos(w0t+µ), где А – амплитуда колебаний, µ - начальная фаза колебаний (определяется тем, ка тело вывели из состояния покоя), w0 – собственная частота колебаний. (w0t+µ) – фаза колебаний.

Свободные колебания — это колебания колебательной системы, совершаемые только благодаря первоначально сообщенной энергии при отсутствии внешних воздействий. (толкнули и отпустили).

Свободные колебания — это колебания колебательной системы, совершаемые благодаря периодическому внешнему воздействию. (постоянно толкают)

Автоколебания - незатухающие колебания, которые могут существовать в какой-либо системе при отсутствии переменного внешнего воздействия, причём амплитуда и период колебаний определяются свойствами самой системы. /Автоколебательные системы – системы, которые сами определяют периодичность внешнего воздействия (механические часы)/

Параметрическими называют колебания, при которых один из параметров физической системы периодически изменяется. /Параметрический резонанс – заключается в совершенном в такт с колебаниями периодическом изменении какого-либо параметра системы, вследствие чего само явление – параметрический резонанс.

Вопрос 21

Гармонические колебания - колебания, при которых смещение колеблющейся точки от положения равновесия изменяется с течением времени по закону синуса или косинуса.

Уравнение и его решение:

Допустим, что в колебательной системе действует только гармоническая сила –kx, F=ma, a=dx2dt2, тогда в дифференциальном виде ур-е будет выглядеть следующим образом:

Разделив на m, и обозначим k/m=w2 получим:

Решением этого ур-я, буду выражения виды:

где A - амплитуда колебаний, t - время, φ - фаза колебаний, w - угловая частота колебаний, w = 2pf = 2p /T, f - частота колебаний, T - период колебаний.

Пружинный маятник - механическая система, состоящая из пружины с коэффициентом упругости k, один конец которой жёстко закреплён, а на втором находится груз массы m.

Если грузик смещён из нулевого положения (в котором пружина не деформирована) на расстояние x, то на грузик со стороны пружины будет действовать сила -kx. На грузик действует сила тяжести mg. Согласно второму закону Ньютона, сумма всех сил, приложенных к грузику, равна ma, где a - ускорение. Дифференциальное уравнение для пружинного маятника будет иметь следующий вид:

md2x/dt2 = -kx + mg, где g - ускорение свободного падения в гравитационном поле, d2x/dt2 - вторая производная координаты x по времени t. Это уравнение имеет следующее решение:

где , Амплитуда колебаний A и фаза колебаний φ зависят от

начальных условий (в момент времени t=0): начального смещение грузика x0 и начальной скорости v0. В состоянии равновесия пружина растянута на величину mg/k.

Амплитуда колебания(А) - есть максимальное за период отклонение колеблющейся величины от среднего за период значения.Частота(ν) (– число колебаний, совершаемый за ед.времени. Фаза(φ) – показывает смещение, сдвиг. Период

17

vk.com/club152685050 | vk.com/id446425943

колебаний(Т) - это наименьший промежуток времени, через который система, соверша­ющая колебания, снова возвращается в то же состояние, в котором она находилась в начальный момент времени, выбранный произвольно.

Вопрос 22

Энергия гармонических колебаний

Кинетическая энергия тела, совершающего гармонические колебания:

Потенциальная энергия тела, совершающего гармонические колебания (под действием квазиупругой силы):

Учитывая, что

можно записать:

Полная энергия гармонических колебаний равна сумме кинетической энергии и потенциальной энергии:

При свободных колебаниях колебательная система получает энергию только в начальный момент времени, а далее энергия системы, а с ней и амплитуда колебаний не меняются. При движении тела кинетическая и потенциальная энергия переходят друг в друга. Когда отклонение системы от положения равновесия максимально, потенциальная энергия максимальна, а кинетическая равна нулю. При прохождении положения равновесия потенциальная энергия достигает минимума, а кинетическая энергия (а с ней и скорость, импульс тела) максимальна.

Вопрос 23

Представление гармонического колебания с помощью векторной диаграммы

Выберем ось Х. Из точки О, взятой на этой оси, отложим вектор длины х0, образующий с осью угол α. Если привести этот вектор во вращение с угловой скоростью w0, то проекция конца вектора на ось Х будет меняться со

временем по закону . Следовательно, проекция конца вектора на ось будет совершать гармонические колебания с амплитудой, равной длине вектора; с круговой частотой, равной угловой скорости вращения, и с начальной фазой, равной углу, образованному вектором с осью X в начальный момент времени.

Сложение гармонических колебаний одного направления

Рассмотрим сложение двух гармонических колебаний одинакового направления и одинаковой частоты, которые имеют следующий вид:

.

Представим оба колебания с помощью векторов х01 и х01. Построим по правилу сложения векторов результирующий вектор х0.

Легко увидеть, что проекция этого вектора на ось Х равна сумме проекций слагаемых векторов х=х1+х2. Следовательно, вектор х0 представляет собой результирующее колебание. Этот вектор вращается с той же угловой скоростью w0, что и векторы х1 и х2, так что результирующее движение будет гармоническим колебанием с частотой w0,

18

vk.com/club152685050 | vk.com/id446425943

амплитудой x0 и начальной фазой α. По теореме косинусов квадрат амплитуды результирующего колебания будет равен

.

Из рис. 7.5 видно, что начальная фаза результирующего колебания будет равна

Итак, представление гармонических колебаний посредством векторов дает возможность свести сложение нескольких колебаний к операции сложения векторов. Формулы можно, получить, сложив выражения для x1 x2 аналитически, но метод векторной диаграммы отличается большей простотой и наглядностью.

Вопрос 24

Найдем результат сложения двух гармонических колебаний одинаковой частоты ω, которые происходят во взаимно перпендикулярных направлениях вдоль осей х и у. Начальная фаза первого колебания равна нулю

где α — разность фаз обоих колебаний, А и В -амплитуды складываемых колебаний. Исключаем из формул t. Запишем складываемые колебания как:

и

Заменим на и на , найдем уравнение эллипса:

Размеры осей эллипса и его ориентация зависят от амплитуд складываемых колебаний и разности фаз α.

Если частоты складываемых взаимно перпендикулярных колебаний имеют различные значения, то замкнутая траектория результирующего колебания довольно сложна. Замкнутые траектории, прочерчиваемые точкой, которая совершает одновременно два взаимно перпендикулярных колебания, называются фигурами Лиссажу. Вид этих замкнутых кривых зависит от соотношения амплитуд, разности фаз и частот складываемых колебаний.

19

vk.com/club152685050 | vk.com/id446425943

Вопрос 25

Затухающие колебания - колебания с постоянно убывающей со временем амплитудой. (из-за потерь энергии в реальной колебательной системе).

Сила сопротивления	где r - коэффициент сопротивления среды.	Знак минус показывает,
что FC направлена в сторону	противоположную скорости. Запишем уравнение колебаний	в точке, колеблющийся в
среде. По второму закону Ньютона

где β - коэффициент затухания. Этот коэффициент характеризует скорость затухания колебаний. При наличии сил сопротивления энергия колеблющейся системы будет постепенно убывать, колебания будут затухать.

x''+βx’+ω02x=0 - дифференциальное уравнение затухающих колебаний.

- уравнение затухающих колебаний (решение).

ω – частота затухающих колебаний:

Период затухающих колебаний:

Коэффициента затухания недостаточна для характеристики затуханий колебаний. Поэтому необходимо ввести такую характеристику для затухания колебаний, в которую входит время одного колебаний. Такой характеристикой является декремент (по-русски: уменьшение) затухания D, который равен отношению амплитуд, отстоящих по времени на период

Логарифмический декремент затухания равен логарифму D:

Логарифмический декремент затухания обратно пропорционален числу колебаний, в результате которых амплитуда колебаний уменьшилась в е раз.

Еще одной характеристикой колебательной система является добротность Q.

Добротность Q колебательной системы называется число, показывающее во сколько раз сила упругости больше силы сопротивления.

Чем больше добротность, тем медленнее происходит затухание, тем затухающие колебания ближе к свободным гармоническим.

При приближении коэффициента затухания к W0 период колебаний становится = +∞ и колебания становятся апериодическими. Выведенная из положения равновесия система возвращается в положение равновесия, не совершая колебаний, запас энергии тела к моменту его возвращения полностью расходуется на преодоление трения.

При приближении коэффициента затухания к собственной частоте W0 период колебаний становится = +∞ и колебания становятся

апериодическими.

Вопрос 26

Если колебательная система подвергается воздействию внешней периодически изменяющейся силы, то возникают вынужденные колебания, имеющие незатухающий характер.

Чтобы в реальной колебательной системе получить незатухающие колебания, надо компенсировать потери энергии. Такая компенсация возможна с помощью какого-либо периодически действующего фактора X(t), изменяющего по гармоническому закону. Для механических колебаний это внешняя вынуждающая сила F=F0 cos wt.

С учетом этого закон движения для пружинного маятника запишется в виде:

Далее через дифференциалы получаем:

20