Введение в многомерный статистический анализ / page175-212 / part2 / part2

6.5. Классификация наблюдений в случае двух

многомерных нормальных генеральных совокупностей,

параметры которых оцениваются по выборке

6.5.1. Критерий классификации. До сих пор мы пред­полагали, что распределения обеих генеральных совокупно­стей известны точно. Но в большинстве приложений этой теории эти распределения являются неизвестными, но они могут быть получены из выборок, по одной из каждой генеральной совокупности. Сейчас мы рассмотрим случай, когда у нас есть выборка из каждой нормальной генераль­ной совокупности, и нам нужно использовать эту информа­цию для того, чтобы решить, над какой из этих двух гене­ральных совокупностей произведено другое наблюдение.

Пусть и — выборки из сово­купностей N() и соответственно. На основе этой информации нам нужно классифицировать на­блюдение х как наблюдение над , или над . Очевидно, наилучшими оценками и ⁽²⁾ являются соответственно и , а лучшей оценкой ма­трицы является матрица S, определяемая из условия

(1)

Подставив эти оценки параметров в (5) § 6.4, получим

. (2)

Первый член (2) является дискриминантной функцией, полученной по двум выборкам

[предложено Фишером [5]]. Это — линейная функция, имеющая наибольшую «дисперсию между выборками» относительно «дисперсии внутри выборок. Мы предлагаем использовать (2) в качестве критерия классификации таким же образом, как используется (5) § 6.4.

В случае, когда распределения, соответствующие гене­ральным совокупностям, известны, можно доказать, что кри­терий классификации является наилучшим в том смысле, что он дает минимум математического ожидания потерь в случае известных априорных вероятностей, и образует класс допу­стимых методов, когда априорные вероятности неизвестны. Использование (2) не может быть оправдано таким же обра­зом. Интуитивно, однако, кажется разумным, что (2) дает хороший результат. В § 6.5.5 предлагается другой критерий.

Предположим, что x₁ . . .,x_N есть выборка либо из , либо из ₂, и нам нужно классифицировать эту выборку как целое. Определим S уравнением

(3)

где

. (4)

Тогда величина, дающая критерий, будет такой:

. (5)

Можно показать, что чем больше N, тем меньше вероят­ности ошибочной классификации.

6.5.2. 0 распределении величины V. Пусть для слу­чайных X, , и S

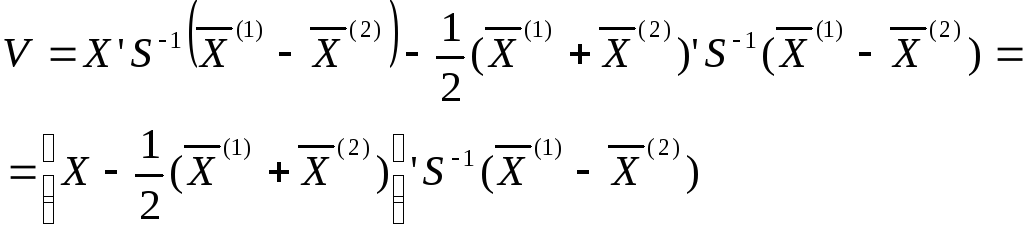. (6)

Распределение величины V слишком сложно. Оно зависит от объемов выборок и неизвестного параметра . Пусть

, (7)

Y =. (8)

Тогда

V = Z'S^-1Y. (9)

Математическое ожидание Y равно , а ковариа­ционная матрица есть [(1/N)+(1/N)]. Вектор Z распре­делен нормально со средним значением

, (10)

если X принадлежит генеральной совокупности , и

, (11)

если X принадлежит генеральной совокупности ₂. Ковариа­ционная матрица в любом случае равна [1+l/(4/N)+1/(4N₂)]. Ковариация между векторами Z и Y равна

(12)

Если = N₂, то эта ковариация равна нулю. Легко видеть, что в этом случае распределение V для X из совпадает с распределением — V для X из ₂. Поэтому, если V0 есть область классификации наблюдения как наблюдения над , то вероятность ошибочной классификации при условии, что X принадлежит , равна вероятности оши­бочной классификации при условии, что X принадлежит ₂.

Распределение V рассмотрено Андерсоном [4], Ситгривесом [1] и Вальдом [2].

6.5.3. Асимптотическое распределение величины V. В случае, когда объемы N и N₂ выборок, произведеных из совокупностей, распределенных N() и , велики, то можно использовать предельные распределения. Поскольку есть среднее значение выборки, состоящей из независимых наблюдений над совокупностью, распре­деленной N(), то, как известно,

. (13)

Точное определение (13) следующее: для любых положитель­ных и можно найти такое N, что для всех NN

(14)

(см. задачу 12 главы 3). Это можно доказать, используя неравенство Чебышева. Аналогично

. (15)

plimS = , (16)

когда , N₂, или когда и N₁ и N_2. Из (16) получаем

plimS. (17)

так как пределы сумм, разностей, произведений и отноше­ний случайных величин по вероятности равны суммам, раз­ностям, произведениям и отношениям соответствующих пре­делов, если только предел каждого знаменателя отличен от нуля (Крамер, [2], стр. 281). Далее

(18)

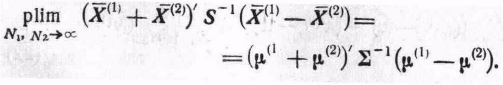(19)

Отсюда следует, что предельное распределение V является распределением U. Для достаточно больших выборок из и ₂ величину можно использовать так же, как если бы мы точно знали распределение генеральных совокупностей, и при этом мы допускаем лишь небольшую ошибку. (Этот резуль­тат впервые был получен Вальдом [2].)

Теорема 6.5.1. Пусть величина V определена равенством (6), где — среднее значение выборки объема n из совокупности N(), — среднее значение выборки объема N₂ из совокупности N (), S — оценка , полученная по объединенной выборке. Тогда предельным распределением V при N₁ и будет , если X распределен N(), и , если X распределен .

6.5.4. Другой вывод критерия. Удобный мнемонический метод вывода критерия основан на использовании регрессии фиктивной величины (предложено Фишером [5]). Пусть

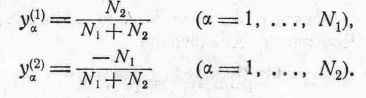
Найдем формально регрессию на величины , выбрав такой вектор b, который дает минимум величины

(20)

где

(21)

«Нормальные уравнения» будут такими:

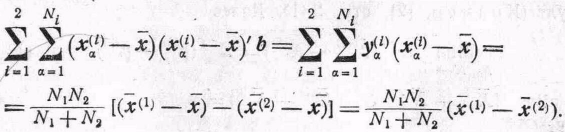
(22)

Матрицу, которая умножается на b, можно записать в виде

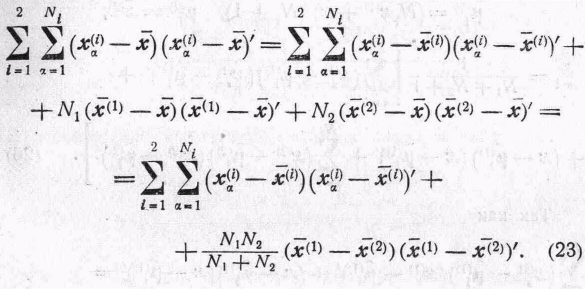
Поэтому (22) можно записать в следующем виде:

(24)

где

(25)

Так как ()'b— скаляр, то вектор b, являющийся

решением (24), пропорционален вектору .

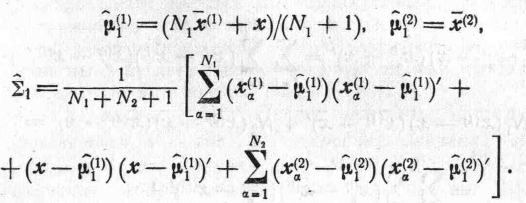(26)

6.5.5. Отношение правдоподобия. Другой величиной, которая может быть использована для критерия классифика­ции наблюдений, является отношение правдоподобия. Пред­положим, что нам нужно проверить составную нулевую гипотезу, состоящую в том, что х, есть выборка из совокупности и — вы­борка из совокупности . Конкурирующая составная гипотеза состоит в том, что — выборка из совокупности , а х, — выборка из совокупности ; , и неизвестны. Если справедлива первая гипотеза, то оценками наибольшего правдоподобия для , и будут

Так как

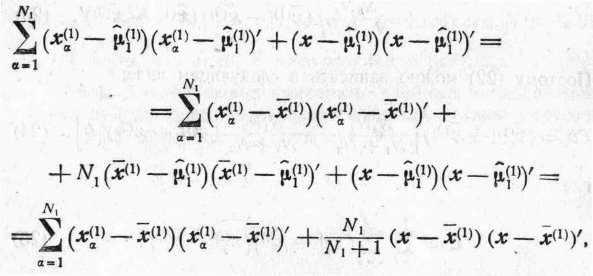
(27)

то , можно выразить таким образом:

(28)

где С определяется по формуле (25). Если предположить, что справедлива конкурирующая гипотеза, то (вследствие симметрии) получим следующие оценки наибольшего правдо­ подобия для параметров: .........

(29)

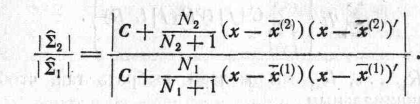
Следовательно, отношение правдоподобия равно (N₁ +N₂ +1)/2-й степени

(30)

Это отношение может быть записано также в виде

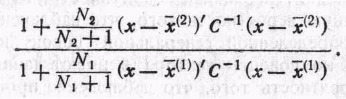(31)

Область, при попадании в которую наблюдение классифици­руется как выборка из , состоит из тех точек, для кото­рых отношение (31) больше заданного числа.