
- •Глава 3 оценка вектора среднего значения и ковариационной матрицы
- •3.1. Введение
- •3.2. Оценки наибольшего правдоподобиядля вектора среднего значения и ковариационной матрицы
- •74 75 3.3. Распределение вектора выборочного среднего; заключение о среднем значении, когда ковариационная матрица известна
- •§ 3.3. Р. Бозе [1], [2]; с. К. Бозе [1], [2]; Даш [1]; Крамер [21; Махаланобис [1], [2]; к. Пирсон [2], [4], [5]; у ил к с [2], [10], стр. 100—101, 103—105, 120—121.
Глава 3 оценка вектора среднего значения и ковариационной матрицы
3.1. Введение
Нормальное распределение
полностью определяется вектором
![]() среднего значения и
ковариационной матрицей
среднего значения и
ковариационной матрицей
![]() .
Первой статистической проблемой является
вопрос о том, как оценить эти параметры
по результатам выборки. В § 3.2 показано,
что оценкой наибольшего правдоподобия
для
.
Первой статистической проблемой является
вопрос о том, как оценить эти параметры
по результатам выборки. В § 3.2 показано,
что оценкой наибольшего правдоподобия
для![]() является выборочное
среднее, оценка наибольшего правдоподобия
для
является выборочное
среднее, оценка наибольшего правдоподобия
для
![]() пропорциональна
матрице, состоящей из выборочных
дисперсий и ковариаций. Выборочная
дисперсия равна сумме квадратов
отклонений наблюденных значений от
выборочного среднего, деленной на число
наблюдений без единицы; выборочная
ковариация определяется подобным же
образом по результатам взаимных
произведений соответствующих
отклонений. Выборочная ковариационная
матрица является несмещенной оценкой
пропорциональна
матрице, состоящей из выборочных
дисперсий и ковариаций. Выборочная
дисперсия равна сумме квадратов
отклонений наблюденных значений от
выборочного среднего, деленной на число
наблюдений без единицы; выборочная
ковариация определяется подобным же
образом по результатам взаимных
произведений соответствующих
отклонений. Выборочная ковариационная
матрица является несмещенной оценкой![]() .
.
Распределение вектора
выборочного среднего дано в § 3.3, и
показано, как может быть проверена
гипотеза, что
![]() является данным вектором, если
является данным вектором, если![]() известна. Случай, когда
известна. Случай, когда![]() неизвестна, будет рассмотрен в главе
5.
неизвестна, будет рассмотрен в главе
5.
3.2. Оценки наибольшего правдоподобиядля вектора среднего значения и ковариационной матрицы
Пусть
дана выборка наблюдений (вектор) над
р-мерным (невырожденным) нормальным
распределением, и нас интересуют
оценки вектора
![]() среднего
значения и ковариационной матрицы
среднего
значения и ковариационной матрицы
![]() этого распределения. Мы выведем оценки
наибольшего правдоподобия.
этого распределения. Мы выведем оценки
наибольшего правдоподобия.
Оказывается, что метод наибольшего правдоподобия очень полезен для различных оценок и проблем проверки гипотез, относящихся к многомерным нормальным распределениям. Оценки, полученные по методу наибольшего правдоподобия, или их модификации обычно обладают некоторыми оптимальными свойствами. В частном случае, изучаемом здесь, оценки асимптотически эффективны (Крамер [2], § 33.3).
Допустим,
что выборка из N
наблюдений
над X,
распределенным
N(![]() ,
,![]() ),
есть x1,
....
xN,
где
N>p.
Функция
правдоподобия будет равна
),
есть x1,
....
xN,
где
N>p.
Функция
правдоподобия будет равна
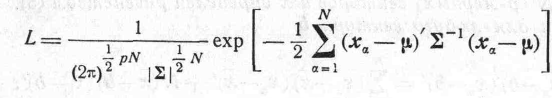
(1)
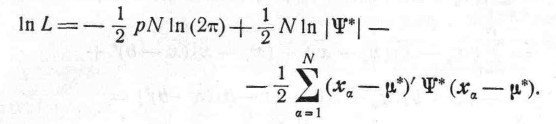
![]() ,
определим сперва оценки наибольшего
правдоподобия для
,
определим сперва оценки наибольшего
правдоподобия для
![]() и
и
![]() =
=![]() .
В функции правдоподобия векторыx1,
..., xN
фиксированы
как значения выборки и L
является
функцией
.
В функции правдоподобия векторыx1,
..., xN
фиксированы
как значения выборки и L
является
функцией
![]() и
и
![]() . Чтобы
подчеркнуть, что величины
. Чтобы
подчеркнуть, что величины
![]() и
и
![]() являются
переменными (а не параметрами), мы
обозначим их через
являются
переменными (а не параметрами), мы
обозначим их через
![]() и
и![]() .
Тогда
логарифм функции правдоподобия будет
равен
.
Тогда
логарифм функции правдоподобия будет
равен
(2)
Поскольку
In
L
является
возрастающей функцией L,
то
ее максимум находится в той же точке
пространства
![]() ,
,![]() что и максимумL.
что и максимумL.
Пусть выборочное среднее равно
(3)
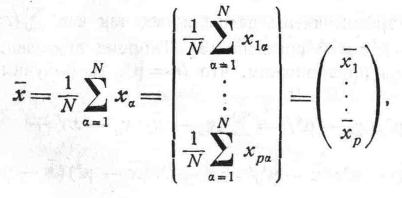
и матрица сумм квадратов и попарных произведений отклонений величин от среднего значения равна
 (4)
(4)
Будет удобно воспользоваться следующей леммой.
Лемма
3.2.1. Пусть
x1,
..., xN
представляют
собой N (р-мерных) векторов и
![]()
определен равенством (3). Тогда для любого вектора b
![]() .
(5)
.
(5)
Доказательство.
![]()
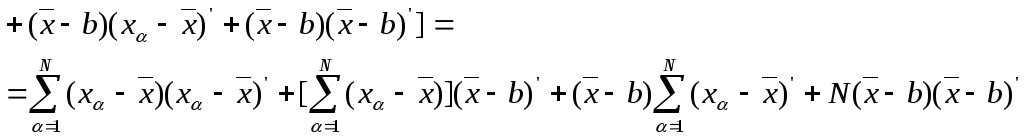 (6)
(6)
Второй
и третий члены равны нулю, так как
![]() согласно (3). Теорема доказана.
согласно (3). Теорема доказана.
Если
мы предположим, что b=![]() ,
то получим
,
то получим
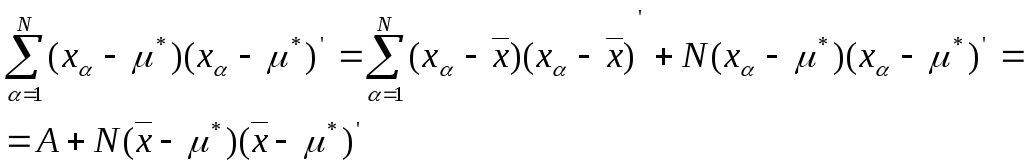 (7)
(7)
Используя
этот результат и свойства следа
матрицы (spCD
=
![]() =spDC),
получим
=spDC),
получим
![]()
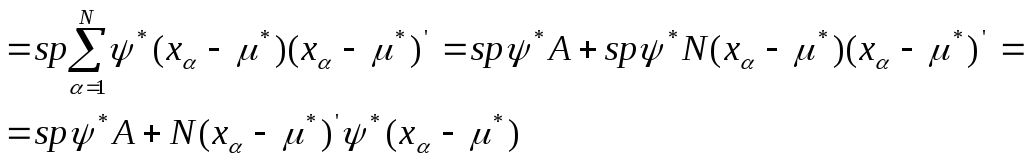
(8)
Тогда мы можем записать (2) следующим образом:
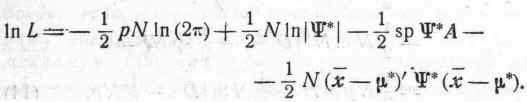 (9)
(9)
Поскольку
матрица
![]() *
неотрицательно определена, то
*
неотрицательно определена, то
![]() и равна нулю, когда
и равна нулю, когда
![]() .
Для определения максимума второго и
третьего членов (9) применим следующую
лемму (которая применяется также в
последующих главах).
.
Для определения максимума второго и
третьего членов (9) применим следующую
лемму (которая применяется также в
последующих главах).
Лемма 3.2.2. Пусть :.
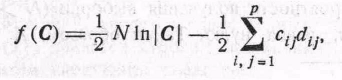 (10)
(10)
где
![]() является неотрицательно определенной
иD
= (d
является неотрицательно определенной
иD
= (d![]() )
положительно определена. Тогда максимум
f(С)
получается
при C=ND-1
и равен
)
положительно определена. Тогда максимум
f(С)
получается
при C=ND-1
и равен
![]() (11)
(11)
Доказательство.
Заметим,
что
![]() ,
если
|С|
,
если
|С|![]() 0
или если один или несколько элементов
С всестремятся
к
0
или если один или несколько элементов
С всестремятся
к
![]() или
или![]() (недиагональные элементы)1).
Максимумы
(недиагональные элементы)1).
Максимумы
![]() (С)
находят, приравнивая нулю производные
(С)
находят, приравнивая нулю производные![]() (С) по элементамС.
Применив
теорему 7 приложения 1, получим
(С) по элементамС.
Применив
теорему 7 приложения 1, получим
![]() (12)
(12)
где
Ckk
обозначает
алгебраическое дополнение ckk
в
С.
Для
k![]() l
l
![]() (13)
(13)
так
как ckl
= clk.
.Приравняв
2df/dckk
и
df/dckl
нулю
и учтя, что Ckl/![]() является
элементом l-й
строки
k-го
столбца С, получим NC-1
= D.
Отсюда
С=
является
элементом l-й
строки
k-го
столбца С, получим NC-1
= D.
Отсюда
С=![]() .
Значение максимума равно
.
Значение максимума равно
f(ND-1)
=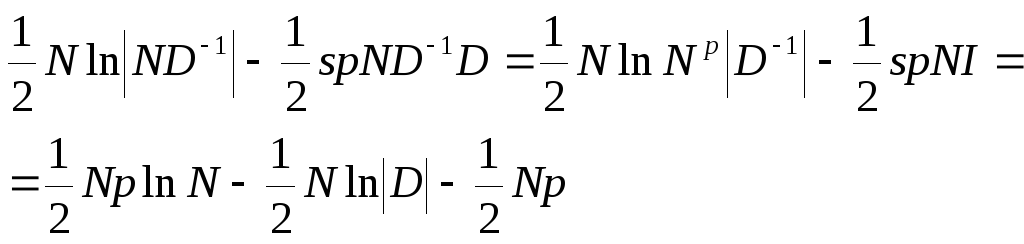 .
(14)
.
(14)
Применив эту лемму к (9), где последний член равен нулю, обнаружим, что
максимум достигается при
![]() (15)
(15)
Мы
предположим, что А
невырожденная;
в главе 7 мы увидим, что вероятность
получения выборки (N
>
р),
когда
А
вырожденная,
равна нулю. Таким образом,
![]() существуети
существуети
![]() *
положительно определена. Поэтому
*
положительно определена. Поэтому![]() является единственным значением
является единственным значением![]() *,
которое обращает последний член (9) в
нуль. Таким образом, оценками наибольшего
правдоподобия для
*,
которое обращает последний член (9) в
нуль. Таким образом, оценками наибольшего
правдоподобия для![]() и
и![]() служат
служат
![]() и
и![]() .
.
Для
нахождения оценки наибольшего
правдоподобия для
![]() нам понадобится следующая лемма.
нам понадобится следующая лемма.
Лемма
3.2.3. Пусть
![]() —
вещественная
функция, определенная на некотором
множестве S,
и
—
вещественная
функция, определенная на некотором
множестве S,
и
![]() — однозначная
функция, имеющая однозначную обратную
функцию, определенная на S
со значениями на некотором другом
множестве S*;
т. е. каждому
— однозначная
функция, имеющая однозначную обратную
функцию, определенная на S
со значениями на некотором другом
множестве S*;
т. е. каждому
![]() S
соответствует
единственное
S
соответствует
единственное
![]() S*
и,
обратно, каждому
S*
и,
обратно, каждому
![]() S*
соответствует
единственное
S*
соответствует
единственное
![]() S
.
S
.
Пусть
![]() (16)
(16)
Тогда,
если
![]() достигает
максимума при
достигает
максимума при
![]() ,
то
,
то
![]() достигает
максимума при
достигает
максимума при![]() .
Если
максимум
.
Если
максимум
![]() при
при
![]() является
единственным, то максимум
является
единственным, то максимум
![]() при
при![]() также
будет единственным.
также
будет единственным.
Доказательство. По предположению,
![]() (17)
(17)
для
всех
![]() S.
Тогда для любого
S.
Тогда для любого
![]()
![]() (18)
(18)
Таким
образом
![]() ,
достигает максимума при
,
достигает максимума при
![]() .
Если максимум
.
Если максимум
![]() при
при
![]() является единственным, то при
является единственным, то при![]() неравенство
(17) является строгим, и максимум
неравенство
(17) является строгим, и максимум
![]() единственный. Имеем следующее
следствие.
единственный. Имеем следующее
следствие.
Следствие
3.2.1. Если
для данной выборки
![]() являются
оценками наибольшего правдоподобия
параметров распределения
являются
оценками наибольшего правдоподобия
параметров распределения
![]() ,
то
,
то
![]() (
(![]() ),…
),…![]() (
(![]() )
являются
оценками наибольшего правдоподобия
для
)
являются
оценками наибольшего правдоподобия
для
![]() (
(![]() ),…
),…![]() (
(![]() ),если
пре
образование
),если
пре
образование![]()
![]() в
в![]() ,…
,…![]() является
взаимнооднозначным. Если оценки
является
взаимнооднозначным. Если оценки![]() являются
единственными, то оценки
являются
единственными, то оценки
![]() ,…
,…![]() также
являются
единственными.
также
являются
единственными.
Из
следствия видно, что оценкой наибольшего
правдоподобия для
![]() является
является![]() .
Обобщим
полученные результаты в следующей
теореме.
.
Обобщим
полученные результаты в следующей
теореме.
Теорема
3.2.1. Если
x1
..., xN
— выборка из N(![]() )
(p
<
N),
то оценками
)
(p
<
N),
то оценками
наибольшего
правдоподобия для
![]() и
и
![]() являются
величины
являются
величины
![]() =
=![]() =
(1/N)
=
(1/N)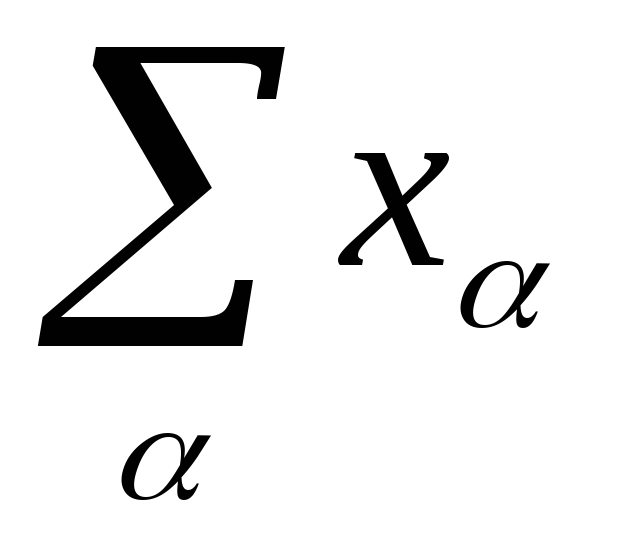
и
![]() =(1/N)
=(1/N)![]() .
.
Вычисление
оценок
![]() проще производить с помощью специального
случая леммы 3.2.1
проще производить с помощью специального
случая леммы 3.2.1
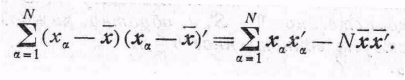 (19)
(19)
Элемент
![]() вычисляется, как элемент
вычисляется, как элемент![]() ,
и элементN
,
и элементN![]() вычисляется,
как N
вычисляется,
как N![]() или
или
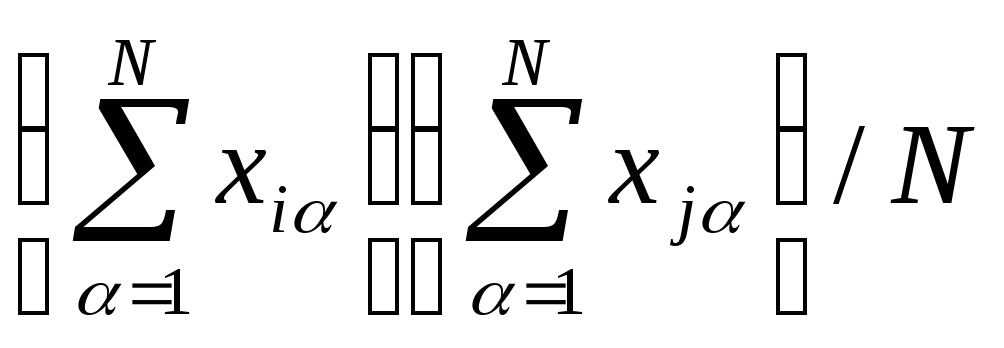 .
.
Следствие
3.2.2. Если
![]() ,
…,
,
…,![]() образуют
выборку из N(
образуют
выборку из N(![]() ),где
),где![]() (
(![]() ),то
оценкойнаибольшего
правдоподобия для
),то
оценкойнаибольшего
правдоподобия для
![]() является
является
![]() =
=![]() оценкой
наибольшего правдоподобия для
оценкой
наибольшего правдоподобия для![]() является
является
![]() ,где
,где
![]() естьi-я
компонента
ха
и
естьi-я
компонента
ха
и
![]() естьi-я
компонента
естьi-я
компонента
![]() ,
а оценка наибольшего правдоподобия для
,
а оценка наибольшего правдоподобия для![]() равна .
равна .
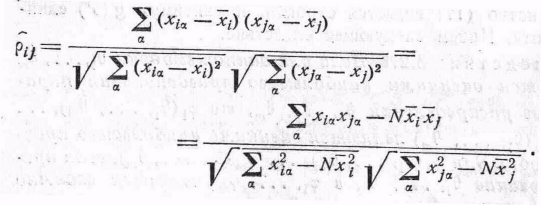 (20)
(20)
Доказательство.
Множество параметров
![]() и
и![]() является
взаимнооднозначнымпреобразованием
множества параметров
является
взаимнооднозначнымпреобразованием
множества параметров
![]() и
и![]() .
Поэтому,
согласно следствию 3.2.1, оценкой для
.
Поэтому,
согласно следствию 3.2.1, оценкой для
![]() является
является![]() ,
оценкой для
,
оценкой для![]() является
является![]() ,
а
оценкой для
,
а
оценкой для
![]() является
,
является
,
![]() (21)
(21)
К.
Пирсон [1] доказал справедливость этой
оценки для
![]() ,
и
(20) иногда называется коэффициентом
корреляции Пирсона. Обычно он обозначается
через rl}.
,
и
(20) иногда называется коэффициентом
корреляции Пирсона. Обычно он обозначается
через rl}.
Рис.2 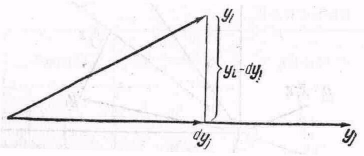
Удобна
геометрическая интерпретация векторов
выборки (![]() )=
X
как строк матрицы X.
Пусть
)=
X
как строк матрицы X.
Пусть
(22)
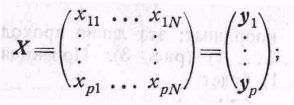 '
'
т. е.
yi
является
i-и
строкой X.
Вектор yi
может рассматриваться как вектор в
N-мерном
пространстве,
![]() -я
координата одного конца которого есть
-я
координата одного конца которого есть![]() и
другой конец которого расположен в
начале координат. Выборка образуетр
векторов
в N-мерном
евклидовом пространстве. Согласно
определению евклидовой метрики,
длина yi
(т.
е. расстояние от одного конца до другого)
есть
и
другой конец которого расположен в
начале координат. Выборка образуетр
векторов
в N-мерном
евклидовом пространстве. Согласно
определению евклидовой метрики,
длина yi
(т.
е. расстояние от одного конца до другого)
есть
![]() .Покажем
теперь, что косинус угла междууi
и
yj
равен
.Покажем
теперь, что косинус угла междууi
и
yj
равен
![]() .
Выберем скалярd
так, чтобы вектор dyj
был
ортогонален вектору
.
Выберем скалярd
так, чтобы вектор dyj
был
ортогонален вектору
![]() ;т.
е. 0 =dyi
(
;т.
е. 0 =dyi
(![]() )'
=
d
(
)'
=
d
(![]() ).
Поэтомуd=
).
Поэтомуd=![]() .Разложим
yi
на уj
— d
yj
и
dyj
(yj
= (yj—dyj)+
d
yj),
как
показано на рис. 2. Ясно, что косинус угла
.Разложим
yi
на уj
— d
yj
и
dyj
(yj
= (yj—dyj)+
d
yj),
как
показано на рис. 2. Ясно, что косинус угла
73
![]()
Это доказывает желаемый результат.
Для
того чтобы дать геометрическую
интерпретацию аii
и
![]() мы
рассмотрим линию, образующую равные
мы
рассмотрим линию, образующую равные
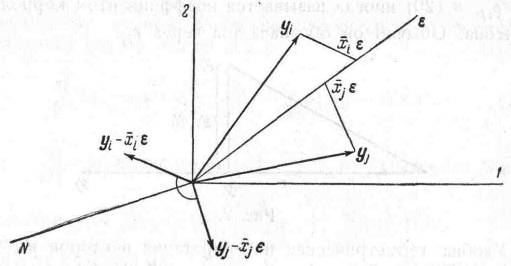
Рис. 3.
углы с осями координат; эта линия проходит через начало и точку (1, 1, ..., 1) (рис. 3).
Проекция
yi
на
вектор
![]() = (1, 1, .... 1) будет
= (1, 1, .... 1) будет
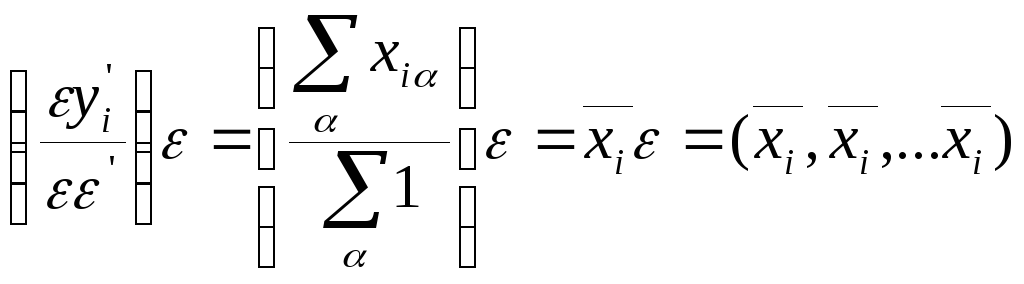
Разложим
уi
на
два вектора:
![]() —
проекцию
yi
на
прямую, образующую равные углы с
координатными осями, и yi
—
—
проекцию
yi
на
прямую, образующую равные углы с
координатными осями, и yi
—![]() проекцию
yi
на
плоскость, перпендикулярную к последней
прямой. Длина yi
—
проекцию
yi
на
плоскость, перпендикулярную к последней
прямой. Длина yi
—
![]() равна
равна
![]() ,
,
т.
е.
N![]() .Перенесем
.Перенесем
![]() и
уj
—
и
уj
—![]() таким
образом, чтобы концы обоих векторов
находились в начале координат; а-я
координата первого вектора будет хjа
—
таким
образом, чтобы концы обоих векторов
находились в начале координат; а-я
координата первого вектора будет хjа
—![]() ,,а
а-я координата второго будет
,,а
а-я координата второго будет
![]() .
Косинус
угла между
.
Косинус
угла между
этими двумя векторами равен
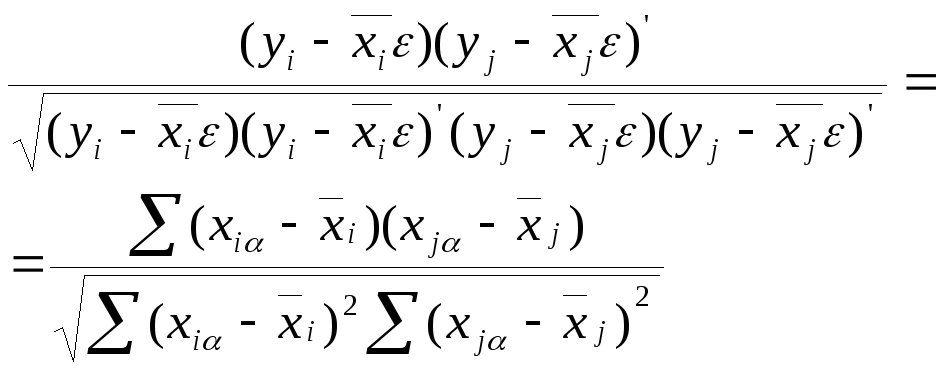
В качестве примера вычислений рассмотрим данные таблицы 1, заимствованные у Стю дента [1].
Таблица!
|
Больной
|
Лекарство А
|
Лекарство В
|
|
|
x
|
|
|
1
|
1,9
|
0,7
|
|
2
|
0,8
|
—1,6
|
|
3
|
1,1
|
-0,2
|
|
4
|
0,1
|
—1,2
|
|
5
|
—0,1
|
—0,1
|
|
6
|
4,4
|
3,4
|
|
7
|
5,5
|
3,7
|
|
8
|
1,6
|
0,8
|
|
9
|
4,6
|
0,0
|
|
10
|
3,4
|
2,0
|
Измерение
x11=
1,9
показывает увеличение времени сна в
часах для первого больного при применении
снотворного лекарства А
и
x21=0,7
— увеличение числа часов сна для первого
больного при применении лекарства В
и
т. д. Предполагая, что каждая пара (т.
е. каждая строка таблицы) является
наблюдением над
![]() ,
мы обнаружим, что
,
мы обнаружим, что
![]() ,
,
![]() ,
(24)
,
(24)
![]()
и
![]() =r12
=0,7952 (S
будет определена ниже).
=r12
=0,7952 (S
будет определена ниже).
