Статистические модели группировки

Статистические модели группировки основываются на вероятностной оценки наших данных , при этом мы предполагаем, что наши данные могут относится к одному из возможных распределений (количеству групп).

Для каждой группы задается априорная вероятность Р1,Р2 ,…Рс Для каждой группы имеется условная плотность распределения:

f ( x / f (x) ) f ( x / ) f ( x / )

1 2 c

Общая функция плотности вероятности определяется следующим образом:

c

f(x) pi f (x / i )

i 1

Мы имеем объекты, которые описываются моделью конечной смеси - это и есть f (x)

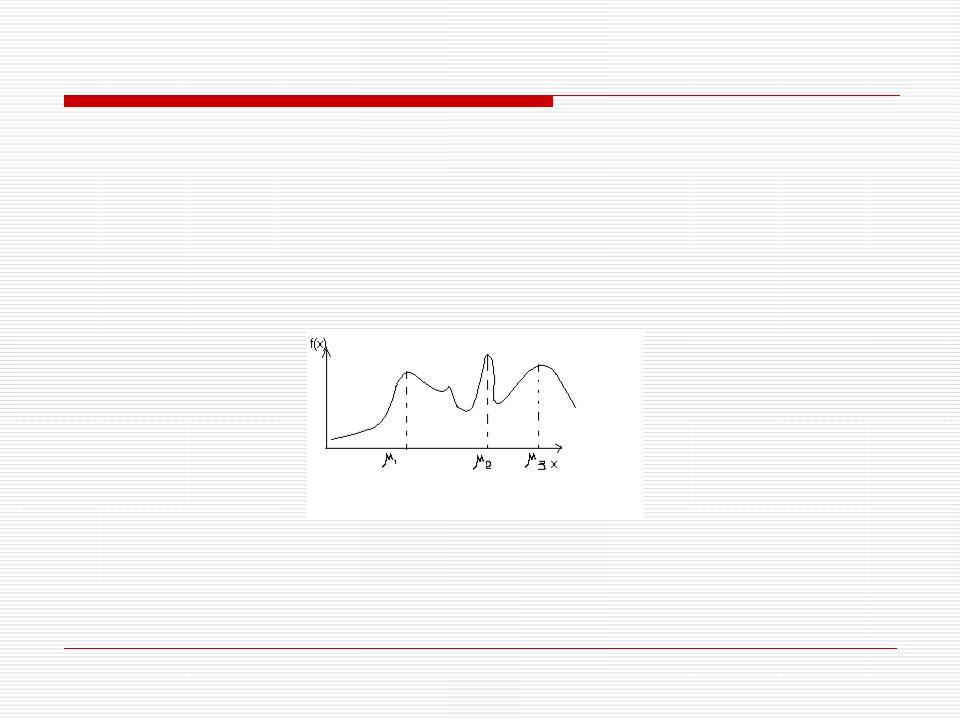
Статистические модели группировки

С точки зрения задачи кластеризации задача ставится следующим образом: есть некоторый многомерный параметр, которым описывается конечная смесь.

(С; p1,p2,…pc, 1 , 2 , c )=- многомерный параметр.

Мы должны оценить вектор этого многомерного параметра.

Каждый максимум соответствует некоторому параметру этой смеси.

Статистические модели группировки

Предполагается, что смесь различима, если можно однозначно восстановить эти параметры.

Восстановить эти параметры можно из условия:

C	C1
pi f (x / i ) p j f (x / j )		x
i 1	j 1

если из этого условия однозначно следует выполнение следующего: 1) С=С1

2) i 1 i C 1 j C

pi p j f (x / i ) f (x / j )

В общем виде эта задача решается как задача оценки многомерного параметра. Лучше всего решать ее по методу максимального правдоподобия

x1 ,......xN

С - известно.		N	C
Строится функция правдоподобия:		L pi f (xk / i )		0 arg max L( )
		k 1	i 1

Статистические модели группировки

Эта задача по постановке и по решению достаточно сложная . Аналитическое решение получить достаточно сложно.

В основном процедуры основаны на рекуррентных методах.

Для случаев нормального распределения и когда С- известно эту задачу можно решать приближенно более простым способом (например методом к-средних).

Метод к-средних позволяет найти центры соответствующих локальных максимумов:

min d(x, mi )

1)Находим mi i =1..C

2) Разбиваем выборку x1 , x2 ,......xN на кластеры

Статистические модели группировки

Далее мы считаем , что метод к-средних дает нам правильное разбиение на кластеры 3) Мы должны для любого i оценить :

1

n

ˆi

j

x j

i 1..C

ni

i 1

x j X i

1

n j

i

(x j

i )(x j

i )T

i 1..C

, где

-матрица ковариации

n

i 1

i

x j X i

pˆi nNi

В результате этой деятельности мы для каждого кластера получаем следующее:

pˆi , ˆi , i

Статистические модели группировки

Далее мы строим f(x) следующим образом:

	c	ˆ
	ˆ
f (x) pi f (x / i , i )
ˆ	i 1		1				1	ˆ T	1	ˆ
f (x / i , i )						exp{		(x i )	i	(x i ) }
			n		1		2
		(2n) 2 ( i ) 2
Мы для заданной выборки						x1 , x2 ,......xN

построим аппроксимацию ее нормального распределения.

Статистические модели группировки

Мы можем найти сложные решающие функции. Это функции равной плотности некоего распределения. Далее функцию сложной плотности можно представить в виде суммы простых функций распределений.

Статистическое решающее правило можно представить в следующем виде:

(x) f1 (x) f2 (x)

c1

pˆi1 f (x / i1 1i )

i 1

c2

pˆi2 f (x / i2 i2 )

i 1

Есть 2 способа провести классификацию:

-отношение правдоподобия

-классификация по минимуму расстояния

ˆ	T
		1	(x i )	расстояние Махланобиса.
(x, X i ) (x i )		i

Алгоритм автоматической классификации на основе кластер-анализа

В данном разделе рассматривается классификации, использующий кластер-анализ для формирования подклассов “сложного класса”.

Алгоритм ориентирован на описание данных с использованием аппроксимации плотностей вероятностей смесью нормальных распределений.

Пусть имеется некоторый класс

,

, ,

z

Предполагаем, что он может быть представлен в виде

1

2

где i i

- подклассы, рассматриваемые как кластеры.

1,z

Пусть ( X ) - плотность распределения, соответствующая классу

fi x

i

- условная плотность распределения, соответствующая подклассу i

i

Pi - априорная вероятность появления объектов из подкласса

Тогда плотность вероятности распределения будет иметь вид

z

i

x Pi fi x

i 1

Алгоритм автоматической классификации на основе кластер-анализа

Логично сделать предположение, что центрами классов формируемого алфавита являются существенные максимумы функции f x

Поэтому цель кластеризации - определить совместную плотность распределения, найти ее существенные максимумы, а следовательно и центры кластеров и тем самым и число кластеров.

Данная задача может быть решена методами стохастической аппроксимации, полагая, что искомая совместная плотность распределения может быть аппроксимирована конечным набором ортонормированных функций f x

^

k

f

x,C

Cj j

x j CT x

j

1,k

j 1

Обозначив через

T

2

C

f

C

x

J

x

dx

X

меру уклонения искомой плотности распределения от истинной, можно сформулировать нашу задачу как задачу нахождения оптимального значения вектора

параметров C C0 , минимизирующего функционал J C

Алгоритм автоматической классификации на основе кластер-анализа

С учетом ортонормированности вектор-функции x оптимальное значение вектора

C0 x f x dx M x

Последнее значение может быть получено по предъявленной на этапе кластеризации
обучающей выборке.		^	x,C0
Найдя C	можно легко определить функцию	f

Анализ которой и определение существенных максимумов дает возможность определить число кластеров, границы кластеров и построить решающее правило кластеризации.

Однако практическая реализация изложенного подхода связана с большими затруднениями, ввиду чего на практике применяется большое количество более простых эвристических алгоритмов.

Поэтому был предложен несколько модифицированный алгоритм класса ISODATA, получивший название алгоритм "адаптивного выбора подклассов" (АВП).