2.8. Приближенное вычисление собственных чисел и векторов корреляционной матрицы.

В задачах обработки часто возникает необходимость в определении собственных векторов корреляционной матрицы, соответствующих тем или иным собственным числам.

Как было оказано, для нахождения собственных чисел и векторов следует найти корни характеристического полинома порядка n относительно ₁, i=1, …n следует найти свой собственный вектор, который мы обозначим как a₁=(a_1i,…a_ni)^r, как решение однородной системы линейных уравнений относительно этого собственного вектора при ограничении на его длину

Но хорошо известно, что точные методы поиска корней полиномы и корней системы линейных уравнений представляют собой громоздкие процедуры при больших n, практически начиная с n3. Поэтому данная задача часто решается итерационными методами вычислительной математики. Итерационные методы для одновременного поиска всех собственных чисел и векторов представляют собой методы преобразования симметричной матрицы в диагональную форму.

При обработке данных на ЭВМ широко используется, в частности, программа EIGEN, включенная первоначально в состав библиотеки научных программ на языке ФОРТРАН (библиотека SSP) для ЭВМ IBM-360/370. В настоящее время данная программа в том или ином виде присутствует в составе математических библиотек (аналогов SSP либо новых разработок) практически для всех языков программирования высокого уровня на всех типах ЭВМ (в частности, на ПЭВМ). В этой программе реализован метод Якоби преобразования действительной симметричной матрицы в диагональную форму. При отсутствии математической библиотеки с данной программой можно использовать её опубликованный текст, переписав в соответствии с правилами выбранного языка программирования.

Часто требуется вычислить только максимальное собственное число и соответствующий ему собственный вектор. Рассмотрим известный итерационный метод приближенного вычисления максимального собственного числа и соответствующего собственного вектора.

Пусть все собственные числа различны и упорядочены ₁>₂>…>_n>0. Пусть x=(x₁,…x_n)^r – некоторый вектор. Совокупность собственных векторов a₁, i=1,…n корреляционной матрицы R образует ортонормированный базис, в пространстве которого вектор x образуется в вектор у, где

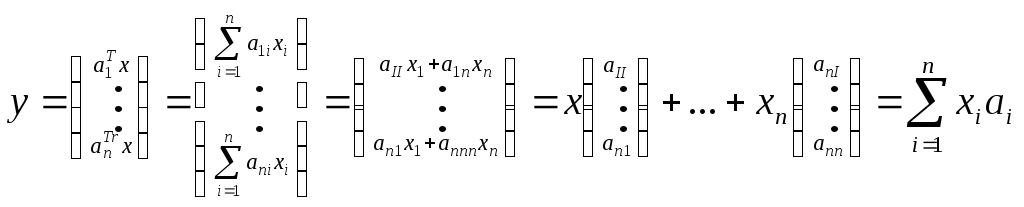
Тогда

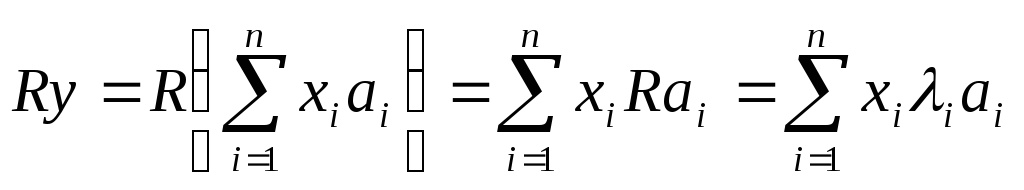
Выделим первое слагаемое

Умножим это равенство еще раз слева на R:

Тогда для некоторогоs получим

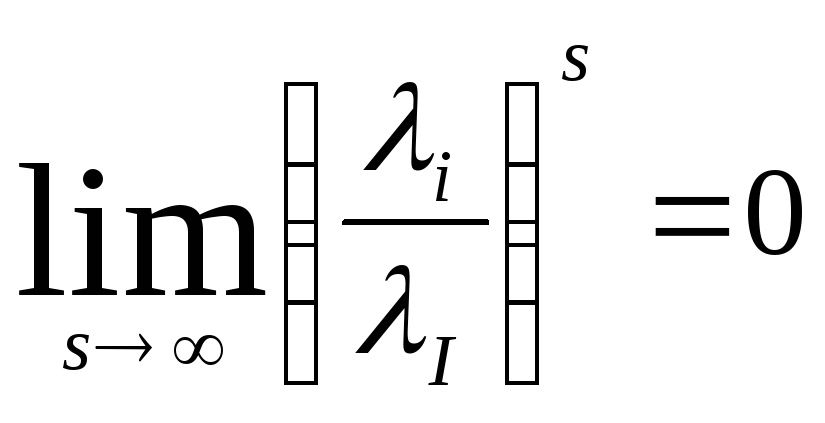Так как ₁>₂>…>_n>0 и , тои

Тогда при х₁0 первый собственный вектор определяется достаточно далеким членом последовательности y, Ry, R²y, …, R^sy, …. Но при ₁>1 получим, что

а при ₁<1 получим, что

Следовательно, векторRsy стремиться по направлению к вектору а1, но его длина значительно отличается от единичной.

Поэтому строят две другие последовательностиy₀, y₁, …y_s, … иz₁,…z_s,…, гдеz_s=Ry_s-1, y_s=z_s/||z_s||, начиная с некоторого вектора у₀единичной длины. Следовательно,||y_s||=1 при любомs, а предел последовательности{y_s} стремится по направлению к вектору а₁. Следовательно,

тогда и.

2.9. Понятие об измерении связи между качественными признаками. Статистический подход.

Как мы уже знаем, качественные признаки возникают при измерениях свойств объектов, например, в номинальной или ранговой шкалах. Пусть два качественных признака измерены в однотипных шкалах. Часто возникает вопрос о существовании или отсутствии связи между ними. Такая ситуация типична, например, при обработке результатов анкетирования. Рассмотрим измерение связи в номинальной шкале.

Пусть N – число наблюдений. Тогда, если в номинальной шкале присутствует r наименований, то N_i/N – относительная частота i-го значений, где .

Типичным является наглядное представление распределения объектов по группам в виде столбиковой диаграммы (гистограммы или полигона частот). В связи с таким представлением данных рассмотрим следующую статистическую задачу.

Пусть выдвинута гипотеза Н о том, что N измерений некоторого признака есть выборка N значений случайной величины с некоторым законом распределения. Если гипотеза Н справедлива, то дискретное распределение выборки можно считать статистической оценкой распределения всей генеральной совокупности. Из-за случайных колебаний эти два распределения не будут совпадать, но можно ожидать, что с ростом N распределение выборки будет приближаться к распределению генеральной совокупности. Тогда следует ввести некоторую меру несовпадения распределений и изучить свойства её выборочного распределения.

Такие меры несовпадения можно конструировать различными способами, но наиболее важной является мера, основанная на критерии ² К.Пирсона.

Пусть p_i>0, i=1,…r – вероятности дискретных значений, где , образующие генеральный закон распределения случайной величины. По методу наименьших квадратов построим меру различия как сумму квадратов отклонений наблюдаемых частот от теоретических, где с_i – произвольные коэффициенты. К.Пирсон показал, что при с_i=N/p_i получается мера расхождения

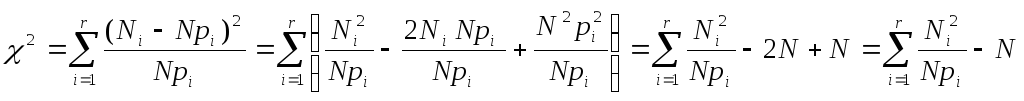распределение которой при N стремится к распределению ².

Вспомним данное распределение. Пусть имеется r независимых нормальных случайных величин x₁…x_r, f(x_i)=N(0,1), i=1…r. Обозначим , а плотность распределения данной суммы как²-распределение.

,

где: x=²- аргумент распределения f(x);

K_r- константа для выполнения условия нормировки

I(n) – гамма-функция, где для целых n>0:

I(1)=1, I(n+1)=n! и ;

r – число степеней свободы.

Вид ² – распределение полностью определяется числом r, а при r>30 практически переходит в нормальное N(r, 2r). Для некоторых распределение r имеет вид (Рис.2.2):

r=1,

r=2,

r=3,

r=4,

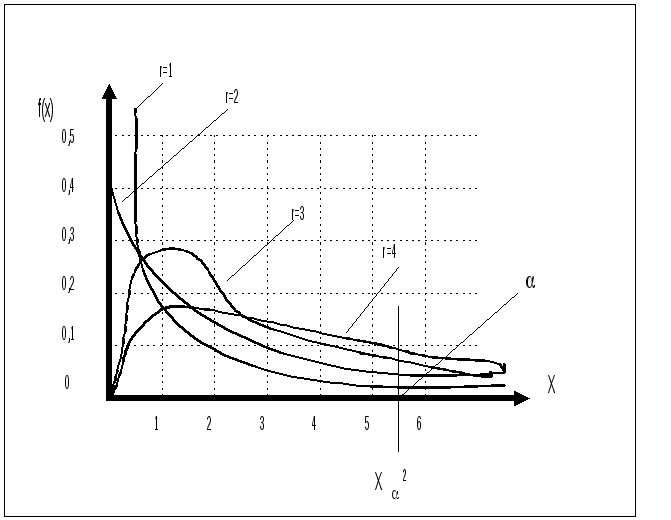
Рис.2.2. Распределение Пирсона

Пусть - значимое значение² с r-1 степенью свободы. Оно определяется так, чтобы вероятность для наблюденного значения ² превысить ²_ равнялось величине

.

Пусть  настолько мало, что можно считать практически достоверным, что при одном испытании событие с вероятностью  не произойдет. Если гипотеза Н верна, то практически невозможно в единственном эксперименте получить значение ² >²_. Если это так, то мы должны признать значит отклонение от гипотезы Н и её отвергнуть.

Вероятность ошибки (отвергнута справедливая гипотеза Н) есть вероятность Р(²>²_)=. Это так называемая ошибка первого рода.

Измерим связь между двумя признаками. Статистическая интерпретация силы связи номинальных признаков основана на критерии ². Пусть даны два таких признака и построены их гистограммы, не обязательно графически, а, например, в виде числового ряда. Совместимое распределение N наблюдений одновременно по r значениям первого признака Х и по s значениям второго признака Y образуют таблицу сопряженности (Рис.2.3), где

N_i и N_j – маргинальные частоты, то есть частоты независимого распределения значений каждого из данных двух признаков.

X/Y	y1 y2 … yj … ys
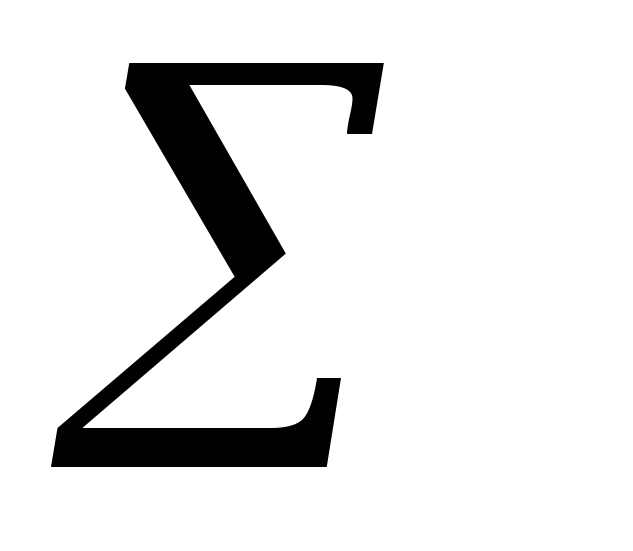
x1 x2 … xi … xr	N11 N12 … Nij … N1s N21 N22 … N2j … N2s Ni1 Ni2 … Nij … Nis Nr1 Nr2 … Nrj … Nrs	N1 N2 Ni Nr
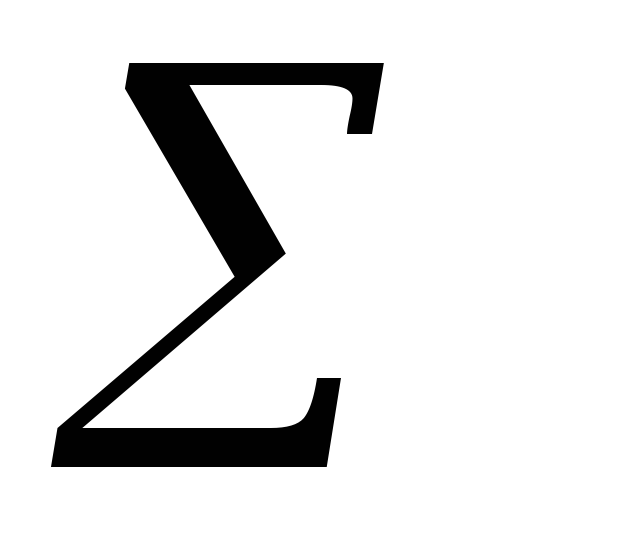
	N1 N2 … Nj … Ns	N

Рис.2.3. Таблица сопряженности двух признаков.

Для такой таблицы требуется проверить гипотезу Н о статистической независимости признаков. Пусть p_ij – вероятность того, что значение x_i признака Х соответствует значению y_j признака Y. Тогда при справедливости гипотезы Н о независимости соблюдается соотношение

для r+s постоянных маргинальных вероятностей p_{i } и p _j. Тогда совместное распределение двух признаков определяется r+s-2 неизвестными параметрами, где из r+s параметров р _i и p _j параметры р _r и p _s можно выразить через остальные .

Вычислим величину ² как величину

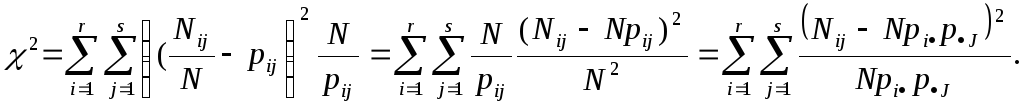
Если справедлива исходная гипотеза Н, то по условию независимости оценки маргинальных частот определяются как р _i =N_i/N, p _j=N_j /N. Тогда получим

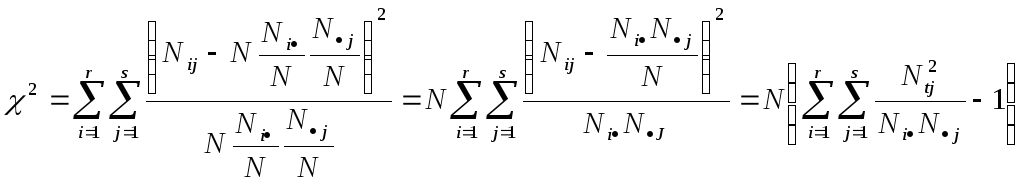
Так как для таблицы сопряженности размером имеется rs переменных значений и r+s-2 параметров, то предельное распределение ², N имеет k=rs-(r=s-2)-1 степеней свободы k=rs-r-s+2-1=rs-r-s+1=r(s-1)-(s-1)=(s-1)(r-1).

Для таблицы размером 2х2 число степеней свободы к=1. Тогда значение ² с 1 степенью свободы на уровне значимости  =0,001 определяет вероятность p(²>²_0,001)=0,001, где ²_0,001=10,827 (найдено по таблице). Следовательно, значение ²10,827 встретится только один раз из 1000 при справедливости гипотезы H о независимости признаков. Поэтому при справедливости гипотезы H крайне мало вероятно (p<0,001), что наблюдаемые и ожидаемые частоты отличаются на столько, величина оценки окажется ²10,827. Если же это так, то гипотезу H следует отвергнуть.

Таким образом, с помощью теста ² можно оценить степень риска (вероятность ошибки первого рода), предполагая существование связи между признаками. Большие значения ² говорят о значимом отклонении от гипотезы независимости, т.е. о связи.

Но в то же время тест ² не дает возможности измерить силу связи. Поэтому для измерения силы связи логично использовать некоторую характеристику, принимающую минимальное значение при отсутствии связи, и максимальное значение при максимальной связи. Критерий ² зависит от объема выборки N. Поэтому Пирсон использовал в качестве меры связи между двумя признаками величину среднеквадратичной сопряженности ²=²/N. При независимости ²=0. Действительно, из следует

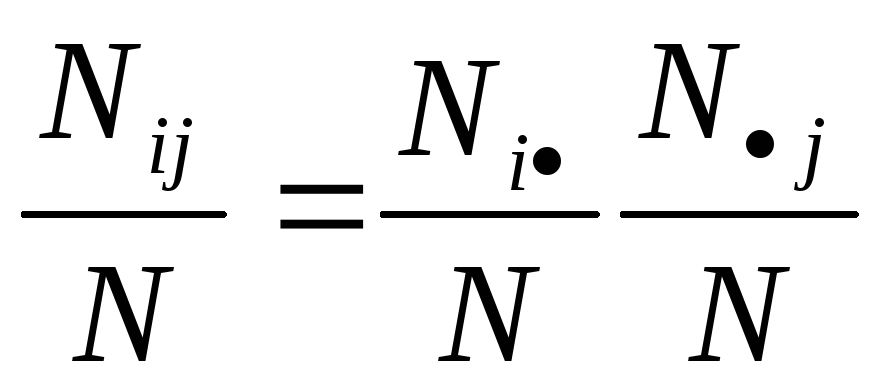и .

Тогда

Найдем максимальное значение ². Очевидно, что справедливо соотношения

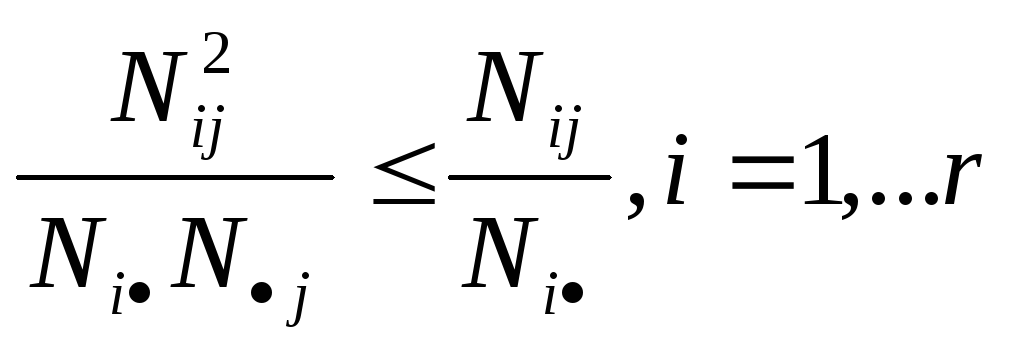и

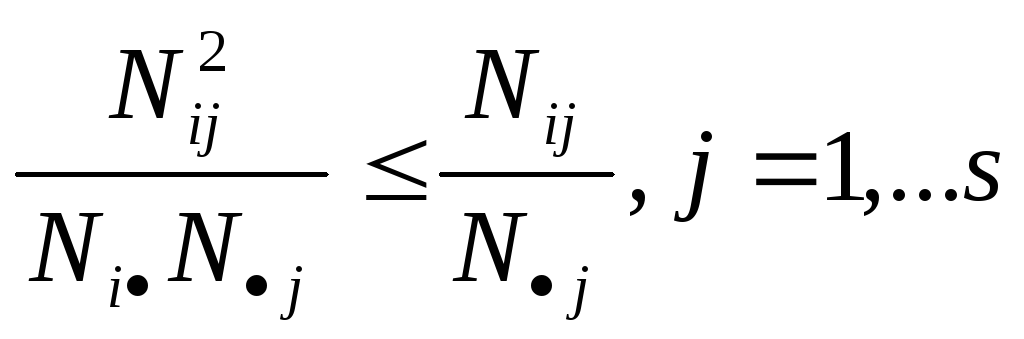
Тогда выполняется соотношения

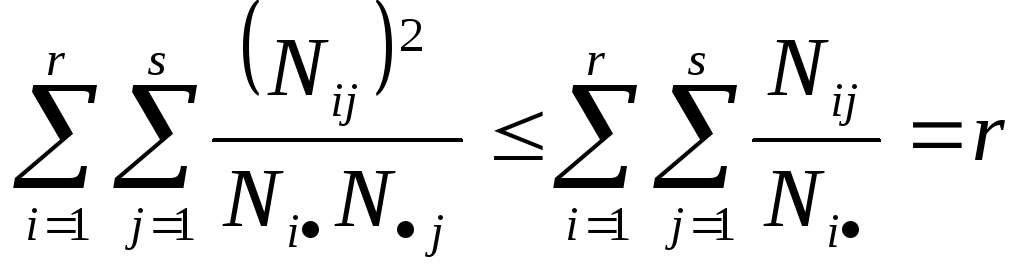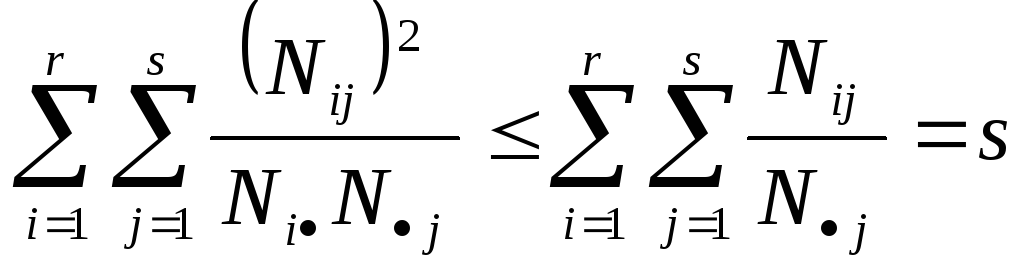, и

Тогда ²  N[min(r,s)-1] = N[min(r-1,s-1)] и окончательно 0²ьшт(r-1,s-1)

Недостаток такой характеристики в том, что при r>2 или s>2 ²>1. Поэтому А.А.Чупровым был предложен коэффициент

где 0T²1.

В свою очередь, коэффициент Чупрова T²=1 только при r=s. Если rs, то даже при полной связи T²<1. Поэтому Г.Крамером был предложен коэффициент

где 0V²1.

Коэффициент Крамера изменяется в данных пределах независимо от размера таблицы сопряженности.