
Рандомизированный алгоритм построения выпуклой оболочки / doc / рандомизированный алгоритм
.docМинистерство образования РФ
Санкт-Петербургский государственный университет
Рандомизированный алгоритм построения выпуклой оболочки
Выполнили:
ст. гр. 0341
Добряков М.М.
Ильина О.К.
Бондарев А.
Санкт-Петербург
2005
Постановка задачи:
Разработать и написать программу рандомизированного алгоритма построения выпуклой оболочки, по исходным данным из дипломной работы. Улучшить визуализацию алгоритма. Добавить подсчёт времени выполнения алгоритма.
Описание Алгоритма.
Обозначим выпуклую оболочку множества точек S через conv(S). Граница conv(S) образует выпуклый многоугольник, вершины которого - подмножество S. Всякий раз, когда нет опасности путаницы, мы будем относиться к этому многоугольнику как к conv(S). Задача вычисления выпуклой оболочки на плоскости состоит в следующем: дано S, требуется вычислить многоугольник (ограничивающий) conv(S). Результат должен быть представлен в виде списка, содержащего точки S, которые являются вершинами conv(S), перечисленные в порядке против часовой стрелки по их появлению в многоугольнике; начальная точка для списка может быть произвольной. Для определенности, будем считать, что первая точка в этом упорядочении - точка из S, имеющая наименьшую x - координату. Для простоты предполагаем, что в S нет трех точек, лежащих на одной прямой. При реализации от этого предположения можно отказаться.
Покажем, как рандомизированная пошаговая конструкция, описанная выше (в разделе 3.1.) в контексте сортировки, может применяться к этой задаче.
Алгоритм сначала случайным образом переставляет точки во входном множестве S. Пусть pi – i-ая точка в этом случайном упорядочении (1 ≤ i ≤ n). Пусть Si - набор {p1, …, pi}. Затем алгоритм продолжается на n шагах. После i-ого шага, алгоритм вычислит conv(Si). На i-ом шаге к conv(Si-1) добавляется pi, формируя conv(Si). Теперь определим подробности этого шага модификации.
пусть мы всегда храним точку во внутренней области conv(S); в частности мы могли бы использовать для этой цели центр масс conv(S3) (который может быть вычислен за постоянное время). Обозначим эту точку p0. Также после i-ого шага мы имеем список, содержащий вершины conv(Si). Кроме того, для простоты описания, мы полагаем, что этот список также содержит ребра, соединяющие последующие вершины в этом списке (этого можно легко избежать в реализации с незначительной дополнительной работой). Пусть S\Si ‑ множество точек, которые должны быть добавлены после i-ого шага, 3 ≤ i ≤ (n-1). Для каждой точки pS\Si, мы сохраняем (двунаправленный) указатель от p на сторону conv(Si), пересекаемую лучом, который исходит из p0 и проходит через p. Мы будем говорить, что p пересекает данное ребро conv(Si). Таким образом, если дано любое ребро conv(Si), мы можем перечислить все точки p, которые пересекают это ребро во времени, линейно зависящем от числа таких точек.
Определив структуры данных, опишем действия, которые требуются для обновления этих структур на каждом шаге. Точка pi, вставленная на i-ом шаге, находится или внутри, или вне conv(Si-1). Используя отрезок pip0 и связанный указатель, мы всегда можем определить положение pi (наше допущение, что никакие три точки не являются коллинеарными, препятствует возможности нахождения pi на границе conv(Si-1)). Если pi находится внутри conv(Si-1), мы удаляем указатель от pi и переходим к шагу (i+1). Иначе, если pi находится вне conv(Si-1), мы должны обновить список, представляющий собой многоугольник, ограничивающий оболочку. Вершины conv(Si-1) разделяются на три множества при добавлении pi:
1. Вершины conv(Si-1), которые должны быть удалены, потому что они не вершины conv(Si).
2. Две вершины conv(Si-1), которые стали соседями pi на conv(Si) (смежные). Обозначим их v1 и v2.
3. Вершины conv(Si-1), которые остаются в conv(Si) с их соответствующими ребрами.
Ясно, что крайние точки ребра , пересеченного отрезком pip0, относятся к (1) или (2). Отходя от (в обе стороны) по списку вершин, представляющему conv(Si-1), мы можем обнаружить вершины типов (1) и (2). Мы делаем так во времени, линейно зависящем от числа таких вершин. Пока мы так делаем, мы обнаруживаем точки S\Si, которые пересекают уже удаленные ребра, и обновляем их указатели, указывая их или на ребро piv1, или на рiv2. Это занимает постоянное время (так как мы должны проверить только два ребра piv1 и piv2) для каждой точки из S\Si, указатель которой должен быть обновлен (рис. 5).

Рис. 5: Выпуклая оболочка conv(Si-1). При добавлении pi к conv(Si-1) вершины s и t удаляются, и указатель для точки q должен быть обновлен, в то время как для r – нет.
Какая полная работа выполнена на i-ом шаге? Стоимость удаления ребра conv(Si-1) равноценна стоимости его создания, так как ребро может быть удалено только однажды после создания. Так как только два ребра создаются на каждом шаге, общее количество этих созданий/удалений ребер (по всем шагам) - в худшем случае 2n.
Что касается стоимости обновления указателей на i-ом шаге, то это число точек p из S\Si, таких что pp0 пересекает ребро, которое удаляется на этом шаге. Чтобы ограничить математическое ожидание этой случайной величины, мы прибегаем к обратному анализу. То есть представим, что алгоритм выполняется назад, и будем удалять точку conv(Si\S3), чтобы сформировать conv(Si-1). Тогда число указателей, обновляемых на i-ом шаге первоначального алгоритма, такое же, как число удаляемых на соответствующем шаге обратного алгоритма. Покажем, что ожидаемое число обновляемых указателей есть O(n/i) в зависимости от любого фиксированного множества Si\S3, из которого мы удаляем случайную точку на обратном шаге. Так как эта верхняя граница имеет силу для любого множества из i точек, зависимость от конкретного множества Si\S3 можно не принимать в расчет.
Для точки p S\Si пусть ep – ребро conv(Si), пересекаемое pp0. Вероятность того, что указатель p обновлен – в точности вероятность того, что ep удалено в результате шага удаления. Ребро ep удаляется, если одна из двух его вершин удаляется на обратном шаге. Так как точка, удаляемая из Si, выбрана равномерно из (i-3) точек из Si\S3, то эта вероятность есть O(1/i). Ожидаемое число обновленных указателей - O((n-i)/i), так что полная работа проделанная на этом шаге есть O(n/i). Ключевым моментом здесь является то, что на шаге удаления обратного алгоритма мы удаляем случайную точку из Si, а не случайную вершину conv(Si). Теперь используем линейность математического ожидания, чтобы ограничить среднее время работы алгоритма O(n log n).
Теорема: Среднее время работы описанного выше рандомизированного алгоритма для вычисления выпуклой оболочки n точек на плоскости - O(n log n).
Среднее время работы данного алгоритма асимптотически то же, что и время некоторых известных детерминированных алгоритмов выпуклой оболочки, в частности алгоритма Грэхема, рассмотренного выше, и соответствует его нижней оценке.
В ходе выполнения курсового проекта из исподников была восстановлена программа реализующая построение выпуклой оболочки с помощью рандомизированного алгоритма.

С помощью меню «Файл» можно сохранять, загружать и очищать множество точек.
С помощью меню «Управление» можно применить алгоритм построения выпуклой оболочки к множеству точек. С помощью подпункта «По шагам» можно по проследить за каждым шагом работы алгоритма. Подпункт «Вернутся в начало» позволяет привести алгоритм в исходное состояние.
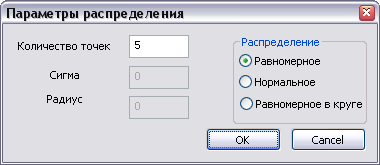
Подпункт «Сгенерировать» позволяет сгенерировать множество точек по заданным законами распределения.
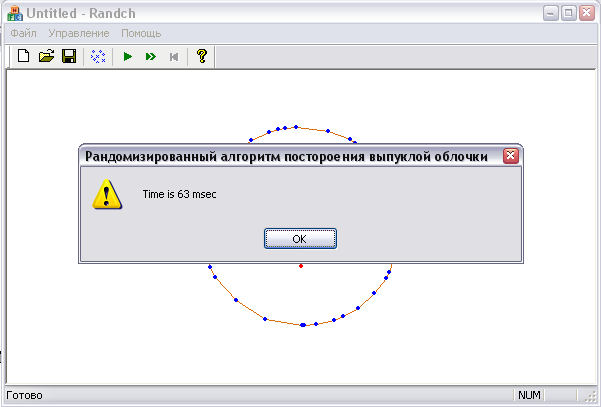
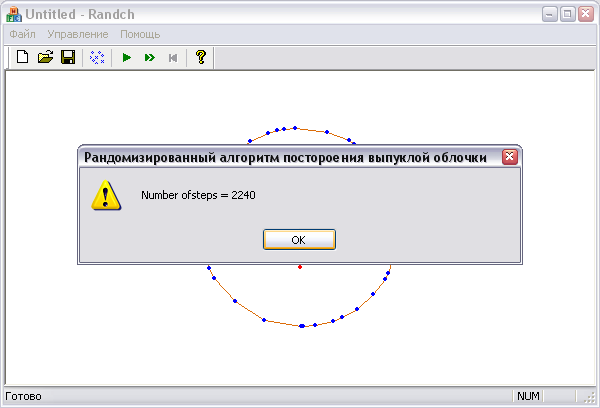
С помощью подпункта «Запуск» можно применить алгоритм построения выпуклой оболочки к множеству точек и посмотреть количество шагов и время за которое был построен выпуклый многоугольник.
Добавления и изменения в программе:
-
Оптимизирован код алгоритма нахождения выпуклой оболочки
-
Русифицированы пункты меню
-
Улучшена визуализация алгоритма (добавлен показ обрабатываемых в текущий момент вершин и рёбер)
-
Добавлено вычисление времени работы алгоритма.
Распределение обязанностей при работе над программой
-
Бондарев А. – написание алгоритма программы.
-
Ильина О.К. – написание интерфейса к программе.
-
Добряков М.М. – написание визуализации программы.
