
Выпуклые оболочки / Алгоритм ЛИ
.docВведение
Как правило, всякий раз, когда на исследуемую задачу накладывается некоторое ограничение, множество рассматриваемых ее индивидуальных экземпляров сокращается. В таких случаях наибольший интерес вызывает вопрос, позволит ли это ограничение разработать специально для этого случая существенно более простой метод по сравнению с общим. Дать убедительный ответ, разработав более простой алгоритм или установив нижнюю оценку сложности решения задачи, аналогичную нижней оценке для общего случая не всегда удается. Но во всех случаях исследования этого вопроса заслуживает внимания.
Примером такой ”ситуации с ограничением” является задача о выпуклой оболочке простого многоугольника.
Определение:
Многоугольник называется простым, если никакая пара непоследовательных ребер не имеет общих точек. Простой многоугольник разбивает плоскость на две непересекающиеся области – внутреннюю (конечную) и внешнюю (бесконечную), разделенные этим многоугольником (теорема Жордана).
Если имеется множество
![]() из
из
![]() точек, то его всегда можно рассматривать
как многоугольник, упорядочив произвольным
образом точки множества и предположив,
что между соседними (с учетом цикличности)
точками получившейся последовательности
имеется ребро. Однако в общем случае
получившийся многоугольник не будет
простым, т.е. некоторые его ребра могут
пересекаться. Но что произойдет, если
известно, что этот многоугольник простой?
точек, то его всегда можно рассматривать
как многоугольник, упорядочив произвольным
образом точки множества и предположив,
что между соседними (с учетом цикличности)
точками получившейся последовательности
имеется ребро. Однако в общем случае
получившийся многоугольник не будет
простым, т.е. некоторые его ребра могут
пересекаться. Но что произойдет, если
известно, что этот многоугольник простой?
Подход, основанный на поиске нижних
оценок, в данной ситуации неприемлем
даже для случая упорядоченной оболочки,
так что следует довольствоваться
тривиальной нижней оценкой
![]() .
Поэтому вполне естественно искать
алгоритмы, имеющие в худшем случае
сложность, меньшую
.
Поэтому вполне естественно искать
алгоритмы, имеющие в худшем случае
сложность, меньшую
![]() .
И ряд таких алгоритмов, каждый со
сложностью
.
И ряд таких алгоритмов, каждый со
сложностью
![]() ,
был предложен. Некоторые из них оказываются
неработоспособными в некоторых очень
частных случаях [Sklansky
(1972); Shamos (1975)] , но другие
алгоритмы правильно решают поставленную
задачу. Среди последних следует упомянуть
довольно сложный алгоритм Маккаллума
– Эйвиса [McCallum, Avis
(1979)], использующий два стека. Впоследствии
были предложены два новых алгоритма,
использующие один стек, - первый Ли
[Lee(1983)], а второй Грэхемом
и Яо [Graham, Yao
1983]. Рассмотрим вариант алгоритма Ли.
,
был предложен. Некоторые из них оказываются
неработоспособными в некоторых очень
частных случаях [Sklansky
(1972); Shamos (1975)] , но другие
алгоритмы правильно решают поставленную
задачу. Среди последних следует упомянуть
довольно сложный алгоритм Маккаллума
– Эйвиса [McCallum, Avis
(1979)], использующий два стека. Впоследствии
были предложены два новых алгоритма,
использующие один стек, - первый Ли
[Lee(1983)], а второй Грэхемом
и Яо [Graham, Yao
1983]. Рассмотрим вариант алгоритма Ли.
Теоретические сведения
Самая левая точка – точка, которая при минимальной абсциссе имеет также максимальную ординату.
Самая правая точка - точка, которая при максимальной абсциссе имеет также минимальную ординату.
Точка находится слева относительно ориентированной прямой:
Пусть даны три точки
![]() ,
не лежащие на одной прямой. Они определяют
треугольник
,
не лежащие на одной прямой. Они определяют
треугольник
![]() ,
который называется положительно
ориентированным, если точка
,
который называется положительно
ориентированным, если точка
![]() лежит слева от отрезка прямой
лежит слева от отрезка прямой
![]() ,
и отрицательно ориентированным,
если точка
,
и отрицательно ориентированным,
если точка
![]() лежит
справа от отрезка прямой
лежит
справа от отрезка прямой
![]() .
Т.к. ориентация треугольника не меняется
при переносе, то определять положение
точки относительно прямой можно с
помощью векторов. Пусть
.
Т.к. ориентация треугольника не меняется
при переносе, то определять положение
точки относительно прямой можно с
помощью векторов. Пусть
![]() и
и
![]() ,
тогда задача сводится к определению
угла
,
тогда задача сводится к определению
угла
![]() между векторами, измеренными в направлении
против часовой стрелки, начиная от
направления вектора
между векторами, измеренными в направлении
против часовой стрелки, начиная от
направления вектора
![]() .
Если
.
Если
![]() ,
тогда
,
тогда
![]() имеет положительную ориентацию, в
противном случае (
имеет положительную ориентацию, в
противном случае (![]() )
треугольник имеет отрицательную
ориентацию.
)
треугольник имеет отрицательную
ориентацию.
Упорядоченная тройка вершин
![]() называется правым поворотом, если
называется правым поворотом, если
![]() находится
справа от прямой, проходящей через
находится
справа от прямой, проходящей через
![]() и
и
![]() с
учетом направления от
с
учетом направления от
![]() к
к
![]() ;
в противном случае она называется левым
поворотом
;
в противном случае она называется левым
поворотом
Нижняя оболочка – нижнее подмножество точек выпуклой оболочки относительно прямой через самую левую и самую правую точки.
Верхняя оболочка – верхнее подмножество точек выпуклой оболочки относительно прямой через самую левую и самую правую точки.
Опорной прямой к выпуклому многоугольнику называется прямая, проходящая через некоторую вершину этого многоугольника таким образом, что его внутренность целиком находится целиком по одну сторону от прямой.
Алгоритм Ли (построение выпуклой оболочки полигона)
Пусть
![]() - самая левая вершина заданного простого
многоугольника, а
- самая левая вершина заданного простого
многоугольника, а
![]() -
упорядоченная циклическая последовательность
его вершин (за вершиной
-
упорядоченная циклическая последовательность
его вершин (за вершиной
![]() следует
следует
![]() ).
Предполагается, что внутренность
).
Предполагается, что внутренность
![]() находится по правую сторону при обходе
его границы в указанном порядке, т.е.
циклическая последовательность вершин
многоугольника ориентированна по
часовой стрелке (рис.1.).
находится по правую сторону при обходе
его границы в указанном порядке, т.е.
циклическая последовательность вершин
многоугольника ориентированна по
часовой стрелке (рис.1.).
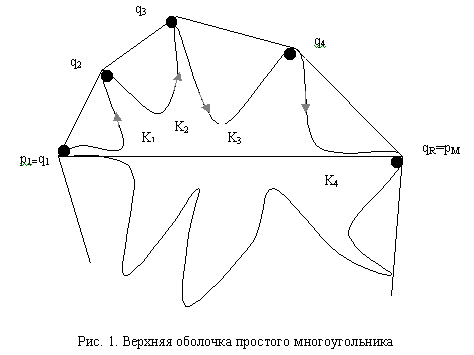
Пусть
![]() -
самая правая вершина. Ясно, что
-
самая правая вершина. Ясно, что
![]() и
и
![]() являются граничными точками выпуклой
оболочки многоугольника
являются граничными точками выпуклой
оболочки многоугольника
![]() .
Кроме того, они разбивают последовательность
вершин многоугольника на две цепи: одна
от
.
Кроме того, они разбивают последовательность
вершин многоугольника на две цепи: одна
от
![]() до
до
![]() ,
другая от
,
другая от![]() до
до
![]() .
Достаточно рассмотреть построение
выпуклой оболочки лишь для цепи
.
Достаточно рассмотреть построение
выпуклой оболочки лишь для цепи
![]() ,
которую согласно использовавшейся
ранее терминологии, будем называть
верхней оболочкой. Пусть
подпоследовательность
,
которую согласно использовавшейся
ранее терминологии, будем называть
верхней оболочкой. Пусть
подпоследовательность
![]() последовательности
последовательности
![]() ,
у которой
,
у которой
![]() и
и
![]() ,
- искомая выпуклая оболочка многоугольника.
Каждое из ребер
,
- искомая выпуклая оболочка многоугольника.
Каждое из ребер
![]()
![]() можно
рассматривать как ”крышку” “кармана”
можно
рассматривать как ”крышку” “кармана”
![]() ,
где карман
,
где карман
![]() -
это подцепочка последовательности
-
это подцепочка последовательности
![]() ,
первой и последней вершинами которой
являются
,
первой и последней вершинами которой
являются
![]() и
и
![]() соответственно.
соответственно.
Алгоритм проходит цепь
![]() и
последовательно строит крышки всех
карманов. Особым событием в ходе работы
алгоритма является обнаружение вершины
типа
и
последовательно строит крышки всех
карманов. Особым событием в ходе работы
алгоритма является обнаружение вершины
типа
![]() ,
образующей карман вместе с последней
найденной вершиной типа
,
образующей карман вместе с последней
найденной вершиной типа
![]() .
Такие вершины
.
Такие вершины
![]() будем называть критическими вершинами.
При этом не каждая критическая вершина
является вершиной окончательной выпуклой
оболочки. Они являются лишь кандидатами
в число таковых. По сути дела, единственное,
что утверждается перед завершением
работы алгоритма, это то, что построенная
к этому моменту последовательность
критических вершин
будем называть критическими вершинами.
При этом не каждая критическая вершина
является вершиной окончательной выпуклой
оболочки. Они являются лишь кандидатами
в число таковых. По сути дела, единственное,
что утверждается перед завершением
работы алгоритма, это то, что построенная
к этому моменту последовательность
критических вершин
![]() согласуется с предложением о простоте
многоугольника
согласуется с предложением о простоте
многоугольника
![]() (более детальная характеристика будет
дана далее). Так что теперь внимание
будет сконцентрировано на процедуре
перехода от одной критической точки к
другой. Эта процедура называется шагом
продвижения.
(более детальная характеристика будет
дана далее). Так что теперь внимание
будет сконцентрировано на процедуре
перехода от одной критической точки к
другой. Эта процедура называется шагом
продвижения.
Предположим, что граница многоугольника
просмотрена от вершины
![]() до
до
![]()
![]()
и вершина
![]() является критической. Соответствующая
ситуация показана на рис.2., где карман
является критической. Соответствующая
ситуация показана на рис.2., где карман
![]() закрыт крышкой
закрыт крышкой
![]() .
.
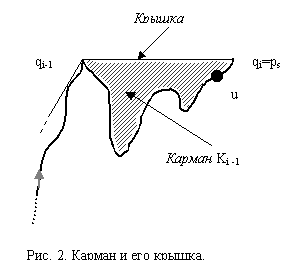
Обозначим через
![]() вершину границы
вершину границы
![]() ,
предшествующую
,
предшествующую
![]() .
В зависимости от положения
.
В зависимости от положения
![]() относительно отрезка
относительно отрезка
![]() имеют место два случая.
имеют место два случая.
-
Вершина
 находится
справа от
находится
справа от
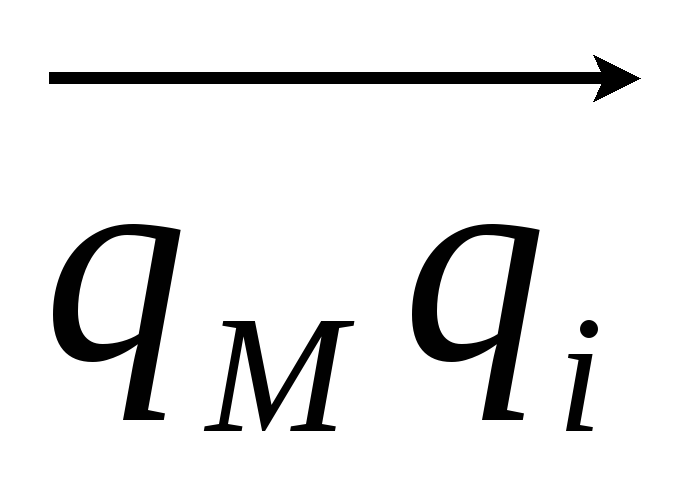 или на нем. В этом случае в вертикальной
полосе, задаваемой вершинами
или на нем. В этом случае в вертикальной
полосе, задаваемой вершинами
 и
и
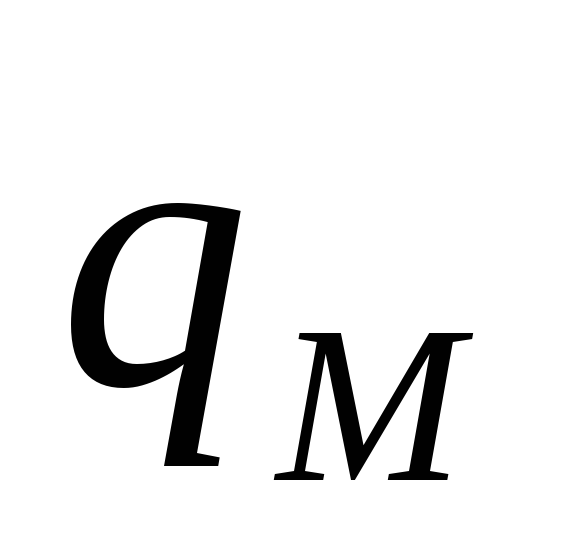 ,
можно рассмотреть и три области,
обозначенные на рис. 4.10 (a)
,
можно рассмотреть и три области,
обозначенные на рис. 4.10 (a)
 ,
,
 и
и
 .
Эти области определяются: прямой,
проходящей через вершины
.
Эти области определяются: прямой,
проходящей через вершины
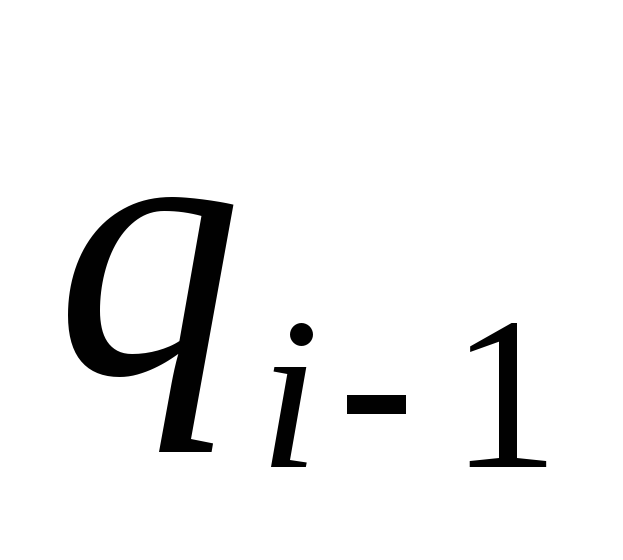 и
и
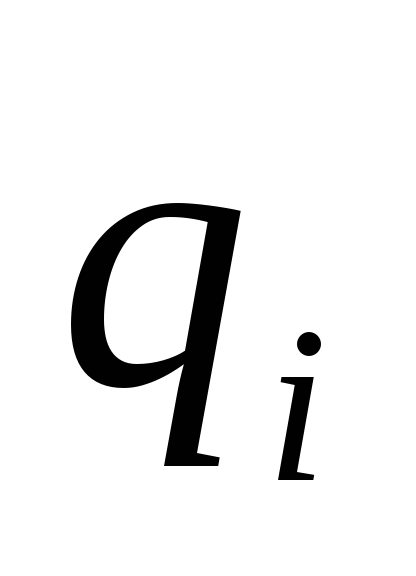 ;
лучом, являющимся продолжением отрезка
;
лучом, являющимся продолжением отрезка
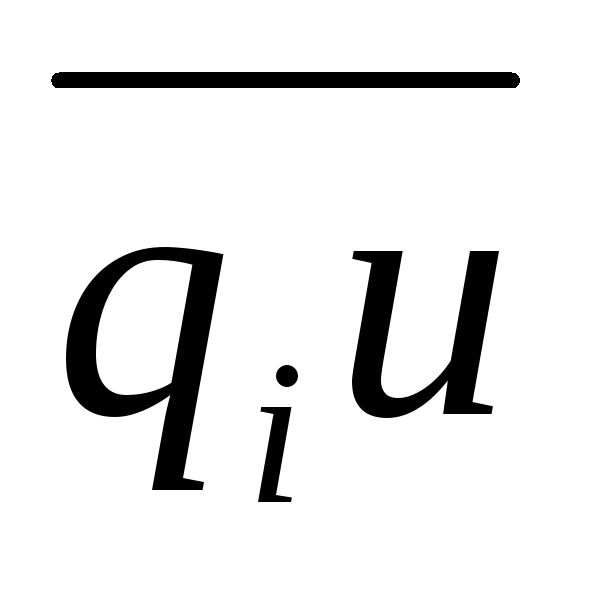 ,
и частью границы многоугольника
,
и частью границы многоугольника
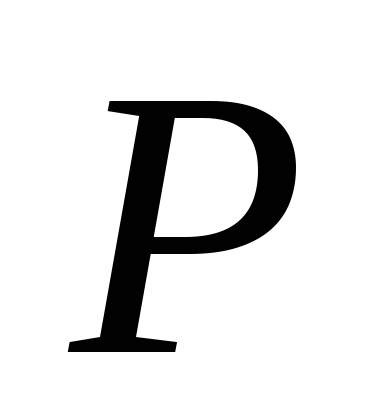 ,
соответствующей карману
,
соответствующей карману
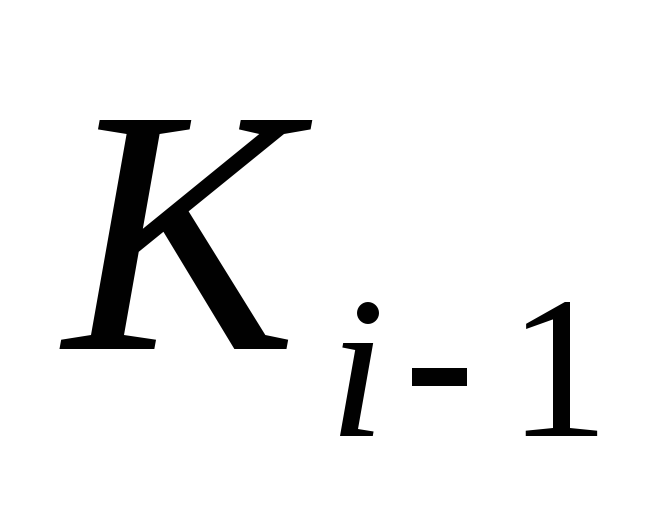 .
.
2. Вершина
![]() находится
слева от
находится
слева от
![]() .
В этом случае в дополнение к предыдущим
определим еще одну область
.
В этом случае в дополнение к предыдущим
определим еще одну область
![]() ,
показанную на рис. 4.10 (b).
,
показанную на рис. 4.10 (b).
Обозначим через
![]() вершину,
следующую за
вершину,
следующую за
![]() на границе многоугольника
на границе многоугольника
![]() .
Вершина
.
Вершина
![]() находится в одной из областей, определенных
выше. Если
находится в одной из областей, определенных
выше. Если
![]() находится в областях
находится в областях
![]() или
или
![]() ,
то она является критической вершиной,
а если она находится в областях
,
то она является критической вершиной,
а если она находится в областях
![]() или
или
![]() ,
то она не является критической. Необходимо
рассмотреть четыре указанных случая
более подробно.
,
то она не является критической. Необходимо
рассмотреть четыре указанных случая
более подробно.

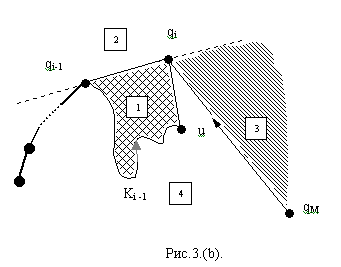
Рис.3. Области, в которых может находиться
вершина
![]() ,
следующая за
,
следующая за
![]() (показаны два случая – в зависимости
от относительного положения
(показаны два случая – в зависимости
от относительного положения
![]() и
и
![]() ).
).
1. Вершина
![]() принадлежит области
принадлежит области
![]() .
В этом случае граница многоугольника
заходит в карман. Будем продвигаться
по границе до тех пор, пока не достигнем
первого
.
В этом случае граница многоугольника
заходит в карман. Будем продвигаться
по границе до тех пор, пока не достигнем
первого
ребра границы, одна из вершин которого
![]() находится вне кармана, т.е. в области
находится вне кармана, т.е. в области
![]()
(рис.4.(a)). Так как многоугольник
![]() простой, а карман и его крышка также
образуют простой многоугольник, то,
согласно теореме о жордановой клетке,
граница многоугольника
простой, а карман и его крышка также
образуют простой многоугольник, то,
согласно теореме о жордановой клетке,
граница многоугольника
![]() обязательно пересечет крышку кармана.
Далее обрабатываем
обязательно пересечет крышку кармана.
Далее обрабатываем
![]() ,
как вершину
,
как вершину
![]() в случае, когда
в случае, когда
![]() принадлежит области
принадлежит области
![]() ,
рассматриваемом ниже.
,
рассматриваемом ниже.

-
Вершина
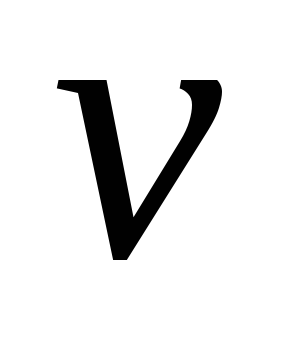 принадлежит области
принадлежит области
 .
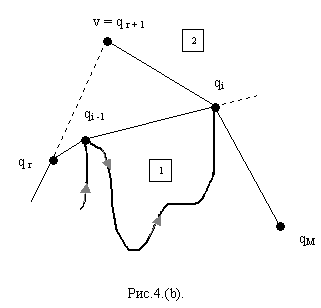
Вершина
.
Вершина
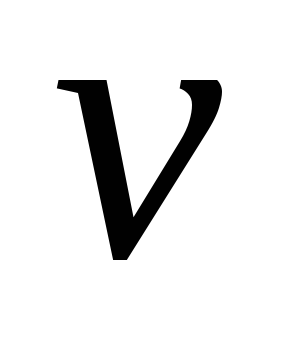 является критической. Ищется опорная
прямая из вершины
является критической. Ищется опорная
прямая из вершины
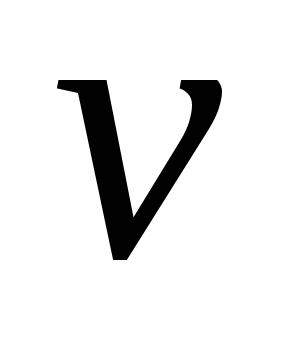 к цепи
к цепи
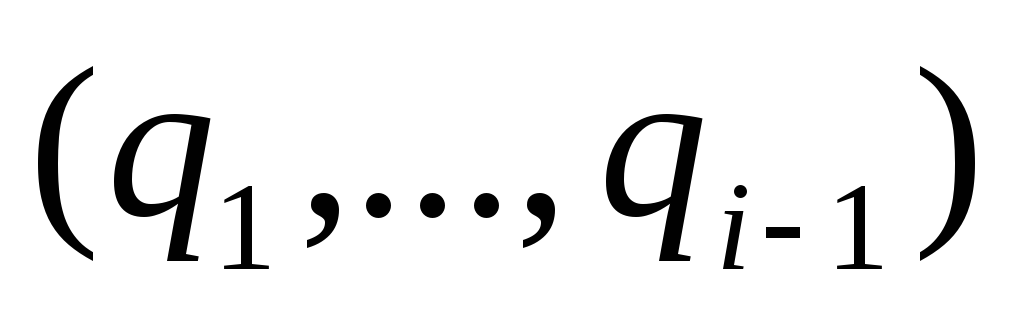 .
Если эта прямая содержит
.
Если эта прямая содержит
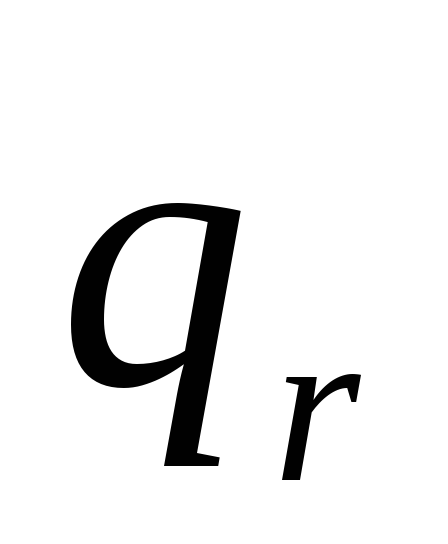
 ,
то вершины
,
то вершины
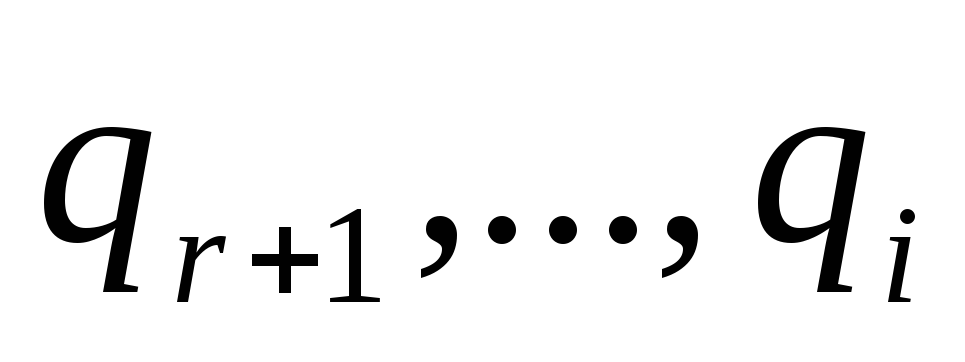 удаляются, а
удаляются, а
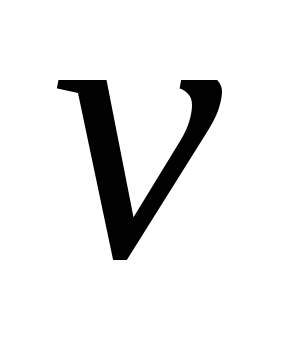 берется в качестве новой
берется в качестве новой
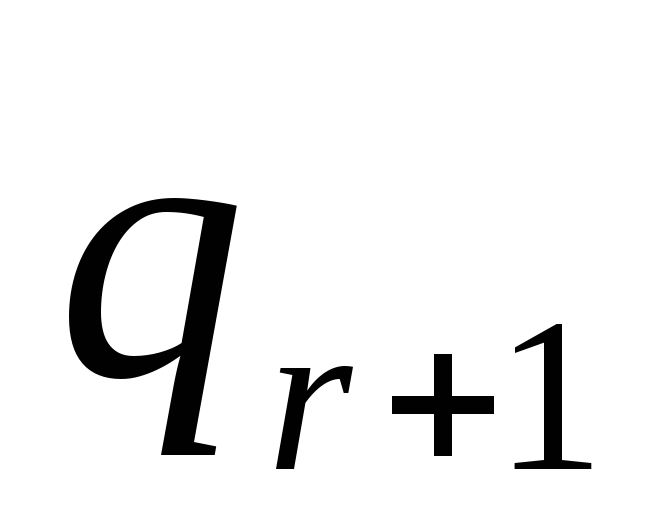 (рис. 4.(b)). Ясно, что
(рис. 4.(b)). Ясно, что
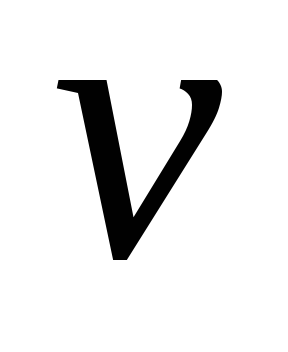 является вершиной выпуклой оболочки
(критической точкой), так как она является
внешней по отношению к текущей оболочке
является вершиной выпуклой оболочки
(критической точкой), так как она является
внешней по отношению к текущей оболочке
 .
Проведение опорной прямой эквивалентно
построению
.
Проведение опорной прямой эквивалентно
построению
 .
.
3. Вершина
![]() принадлежит
области
принадлежит
области
![]() .
Вершина
.
Вершина
![]() является критической, и она берется в
качестве
является критической, и она берется в
качестве
![]() .
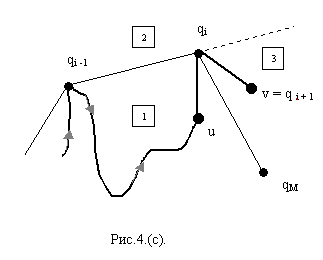
Действительно (рис. 4(с)),
.
Действительно (рис. 4(с)),
![]() является внешней по отношению к текущей
оболочке
является внешней по отношению к текущей
оболочке
![]() ,
и так как она находится справа от прямой,
,
и так как она находится справа от прямой,
проходящей через
![]() и
и
![]() (и ориентированной в направлении от
(и ориентированной в направлении от
![]() к
к
![]() ),
то угол
),
то угол
![]() является выпуклым (при этом (рис.4.(с))
иллюстрирует случай, соответствующий
рис.3.(b).).
является выпуклым (при этом (рис.4.(с))
иллюстрирует случай, соответствующий
рис.3.(b).).
4. Вершина
![]() принадлежит
области
принадлежит
области
![]() .
В этом случае граница многоугольника
заходит внутрь выпуклой оболочки. Как
и в случае 1, рассмотренном выше, будем
продвигаться по границе многоугольника
до тех пор, пока не достигнем первого
ребра, обладающего следующими свойствами:
одна из его вершин является внешней по
отношению к области
.
В этом случае граница многоугольника
заходит внутрь выпуклой оболочки. Как
и в случае 1, рассмотренном выше, будем
продвигаться по границе многоугольника
до тех пор, пока не достигнем первого
ребра, обладающего следующими свойствами:
одна из его вершин является внешней по
отношению к области
![]() или совпадает с
или совпадает с
![]() .
В последнем случае процедура завершается.
В первом же случае вершина, являющаяся
внешней по отношению к области
.
В последнем случае процедура завершается.
В первом же случае вершина, являющаяся
внешней по отношению к области
![]() ,
находится либо в области
,
находится либо в области
![]() (такая ситуация обрабатывается способом,
указанным в пункте 3 выше), либо в области
(такая ситуация обрабатывается способом,
указанным в пункте 3 выше), либо в области
![]() (такая ситуация обрабатывается способом,
указанным в пункте 2 выше) (рис. 4.(d)).
Действительно, обозначим через
(такая ситуация обрабатывается способом,
указанным в пункте 2 выше) (рис. 4.(d)).
Действительно, обозначим через
![]() часть границы многоугольника от
часть границы многоугольника от
![]() до
до
![]() .
.
![]() является простой кривой. Кроме того,
прежде чем она пересечет
является простой кривой. Кроме того,
прежде чем она пересечет
![]() ,
она не может выйти ни в область, находящуюся
справа от вертикальной прямой, проходящей
через
,
она не может выйти ни в область, находящуюся
справа от вертикальной прямой, проходящей
через
![]() ,
ни в облаять, находящуюся слева от
вертикальной прямой, проходящей через
,
ни в облаять, находящуюся слева от
вертикальной прямой, проходящей через
![]() . Так как многоугольник
. Так как многоугольник
![]() простой, то
простой, то
![]() не может пересечь ни одну из границ
карманов
не может пересечь ни одну из границ
карманов
![]() ,
и, следовательно, она не может пересечь
ни одну из крышек этих карманов. Отсюда
следует, что
,
и, следовательно, она не может пересечь
ни одну из крышек этих карманов. Отсюда
следует, что
![]() может пересечь только
может пересечь только
![]() .
Если не пересекает указанный отрезок,
то она заканчивается в точке
.
Если не пересекает указанный отрезок,
то она заканчивается в точке
![]() .
.

Предыдущее обсуждение включает
доказательство корректности любой
реализации, в которой обработка случаев
1 – 4 производится указанным выше
способом. Наиболее подходящими структурами
данных являются: (1) очередь
![]() ,
содержащая последовательность
,
содержащая последовательность
![]() ;
(2) стек Q для хранения
последовательности
;
(2) стек Q для хранения
последовательности
![]() - в виду того, что для вставки и удаления
точек выпуклой оболочки используется
механизм “последний вошел – первый
вышел”, где
- в виду того, что для вставки и удаления
точек выпуклой оболочки используется
механизм “последний вошел – первый
вышел”, где
![]() - фиктивная вершина, имеющая ту же
абсциссу, что и
- фиктивная вершина, имеющая ту же
абсциссу, что и
![]() ,
но меньшую ординату и обеспечивающая
единообразие обработки. Как было сказано
выше,
,
но меньшую ординату и обеспечивающая
единообразие обработки. Как было сказано
выше,
![]() - это вершина на границе многоугольника
- это вершина на границе многоугольника
![]() ,
непосредственно предшествующая вершине
,
непосредственно предшествующая вершине
![]() ,
а вершина
,
а вершина
![]() - текущая вершина. Кроме того, наряду с
обычным использованием операции
- текущая вершина. Кроме того, наряду с
обычным использованием операции
![]() ,
означающей: “ЗАТОЛКНУТЬ
,
означающей: “ЗАТОЛКНУТЬ
![]() в
в
![]() ”,
операция ВЫТОЛКНУТЬ
”,
операция ВЫТОЛКНУТЬ
![]() означает:
”
означает:
”![]() ;
игнорировать
;
игнорировать
![]() ”;
”;
![]() обозначает вершину, находящуюся на
вершине стека, а ПЕРЕДНИЙ(
обозначает вершину, находящуюся на
вершине стека, а ПЕРЕДНИЙ(![]() )
обозначает первый элемент очереди
)
обозначает первый элемент очереди
![]() .
.
procedure ОБОЛОЧКА_МНОГОУГОЛЬНИКА
(p1,…,pM)
-
begin
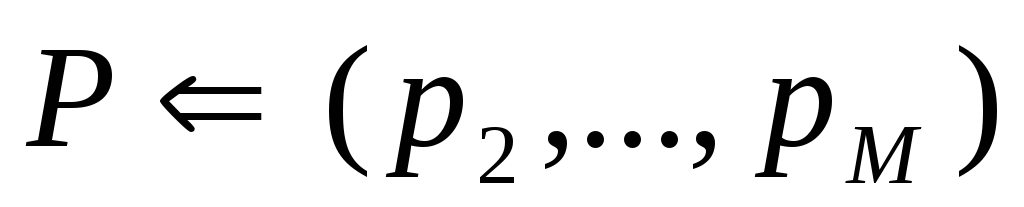 ;
; -
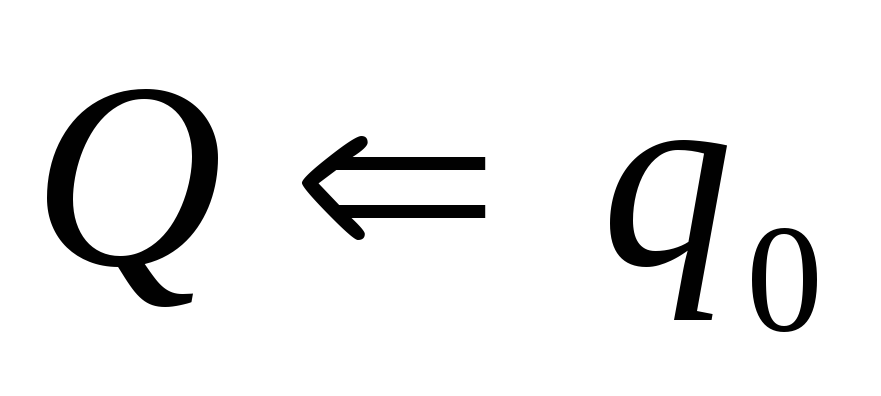 ;
; -
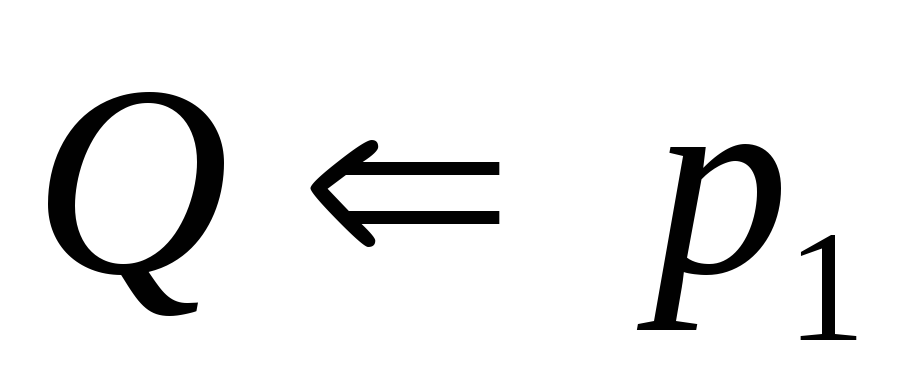 ;
; -
while
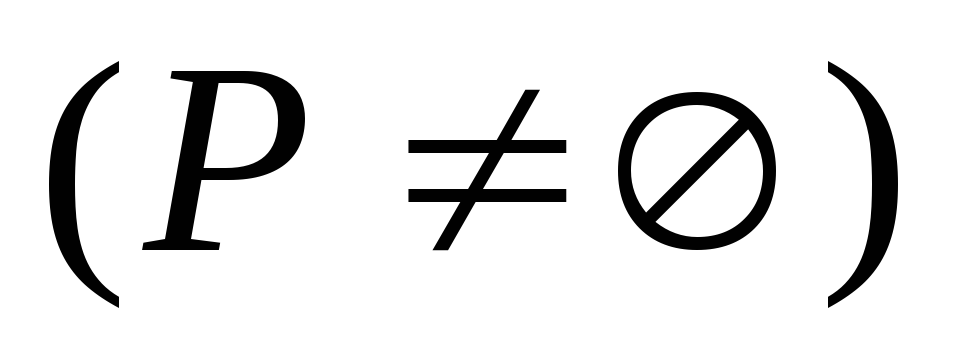 do
do -
begin
 ;
; -
if((qi-1qiv) – правый поворот)
/*области 1, 3, 4*/ then
-
if ((uqiv) – правый поворот /* области 3, 4*/)) then
-
if ((qMqiv) – правый поворот)
/*область 3*/ then
![]()
-
else /*область 4*/
-
while(ПЕРЕДНИЙ(P) находится слева от
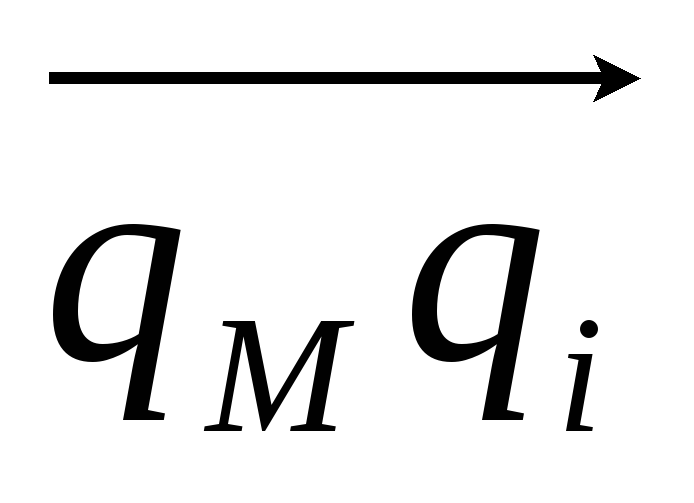 или на нем) do
или на нем) do
ВЫТОЛКНУТЬ P
-
else /*область 1*/
-
while(ПЕРЕДНИЙ(P) находится слева от
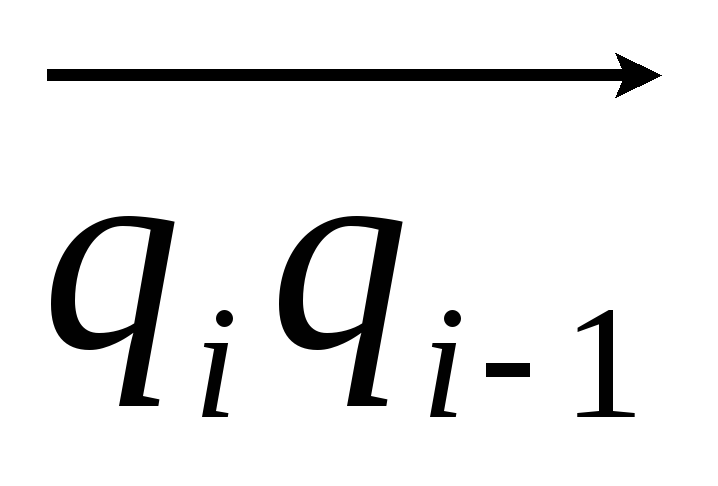 или
на нем ) do
или
на нем ) do
ВЫТОЛКНУТЬ P
-
else /*область 2*/
-
begin while ((qi-1qiv) – левый поворот)
do ВЫТОЛКНУТЬ Q;
15.
![]()
end
end
end.
Анализ сложности алгоритма Ли показывает,
что после инициализации каждая вершина
границы посещается в точности один раз,
прежде чем она будет принята, либо
отвергнута. Обработка каждой вершины
многоугольника осуществляется за
постоянное время. При построении опорной
прямой на каждую операцию удаления
затрачивается постоянное время. Учитывая,
что последовательности
![]() и
и
![]() содержат
содержат
![]() элементов, а рассуждения, аналогичные
приведенным, можно применить и для
построения нижней оболочки многоугольника
элементов, а рассуждения, аналогичные
приведенным, можно применить и для
построения нижней оболочки многоугольника
![]() ,
то в завершение имеем следующую теорему:
,
то в завершение имеем следующую теорему:
Теорема. Выпуклая
оболочка простого многоугольника с
![]() вершинами
может быть построена за оптимальное
время
вершинами
может быть построена за оптимальное
время
![]() при использовании памяти объемом
при использовании памяти объемом
![]() .
.
