30

МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Программометрика

Конспект лекций

для студентов дневного отделения ФБ, АВТФ, ПМИ

Новосибирск

1998

Составитель: к.т.н., доцент кафедры Экономической информатики НГТУ Кайгородцев Г.И.

Рецензент: к.ф.-м.н., доцент кафедры ПСиБД НГТУ Зайцев М.Г.

Работа подготовлена на кафедре Экономической информатики НГТУ

Введение.

Проектирование и управление разработкой программных средств информационных систем (ПС ИС) остается весьма сложной задачей до настоящего времени. Применяющиеся методы оценки объемов ПС ИС и их компонент, трудоемкость, надежность и т.п. базируется, в основном, на использовании сходства или аналогий с предыдущими разработками, классифицированными по соответствующим типам систем, комплексов задач, отдельных процедур и т.д. Отсутствие достаточно надежных аналитических методов расчета параметров ПС приводит к тому, что последние нередко становятся известными только в начале комплексной отладки.

Новые научное и прикладное направление, возникшее в информатике всего два десятилетия назад - метрическая теория программ (программометрика), обеспечило значительное продвижение в решении некоторых из этих проблем.

Современное состояние программометрики позволяет с удовлетворительной для практики точностью решать следующие задачи:

• количественный анализ возможности и целесообразности разработки автоматизированных процедур и функций ИС в заданной постановке;

• численная оценка основных параметров будущего ПС (объем, количество модулей, уровней иерархии, надежность в начальный период эксплуатации) на основе постановок задач;

• Планирование и управление разработкой ПС, оценка трудоемкости его создания, технико-экономическое обоснование;

• решение некоторых вопросов, связанных с метрологией качества ПС.

Данный конспект лекций предназначен для студентов факультетов и специальностей с углубленным изучением информатики (АВТФ, ПМИ, ФБ и др.), а также для специалистов, занимающихся проектированием и разработкой ПС ИС.

Основное внимание здесь уделено так называемым объемным метрикам и, прежде всего, метрике Холстеда, наиболее разработанной и проверенной на практике. Что касается остальных мер сложности программ, в том числе топологических, то обстоятельный обзор их имеется в сборнике [7].

Глава I. Необходимые сведения из алгоритмической теории сложности

1. Определение алгоритмической сложности.

Это понятие играет в информатике такую же фундаментальную роль, как энергия или энгропия в технике. В обычном словоупотреблении термин "сложность" имеет множество оттенков. Математическая формализация данного понятия базируется на идее описания: ясно, что чем сложнее объект, тем длиннее описывающий его текст. Однако решающую роль при таком подходе имеет выбор способа описания. Ограничим, с целью определенности, множество "объектов" различными символьными строками - типичными объектами информатики. Пусть, например,

0011001100110011.....,

101101101101101.......,

1101110010100011..... .

начальные фрагменты двоичных последовательностей. Первые два из них, будучи периодическими, могут быть "описаны" такими псевдопрограммами, как "печать 0011 n раз", "печать 101 n раз", где n - произвольное целое число. Однако в случае третьей последовательности, ввиду ее нерегулярности, может оказаться, что более короткая запись, чем сама последовательность, в принципе невозможна. Возьмем еще один пример. Основание натуральных логарифмов е=2,711828.... имеет бесконечное число цифр, но описывается конечной формулой (алгоритмом)

программа для которой легко может быть написана и имеет небольшую длину. Таким образом, если в качестве объектов будем рассматривать произвольные последовательности символов из некоторого алфавита, то наиболее экономным способом их описания будет алгоритмический. Это соображение позволяет ввести следующее определение сложности объекта [1] (приводим его исключительно ради иллюстрации формально-математического подхода). Пусть  - произвольная частично-рекурсивная функция. Тогда мерой сложности последовательности х назовем величину

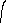
min l(p): (p)=x

_=

, если ps (p)x,

где р - программа (код), по которой  восстанавливает х; l(p) - ее длина (количество двоичных разрядов), а s - множество всех допустимых программ.

Для нашей цели вполне достаточно содержательная трактовка этого определения, состоящая в том, что за меру сложности произвольной последовательности символов из некоторого фиксированного алфавита принимается длина (количество двоичных разрядов) самой короткой программы, генерирующей эту последовательность (как это показано в приведенных выше примерах).

2. Свойства алгоритмической сложности.

Непосредственно из определения вытекают следующие свойства:

1. _l(x),

т.е. сложность последовательности х не превосходит ее длины.

2. lim K_= 

• сложность последовательности, в общем случае, неограниченно расчет с ее длиной. Интуитивно ясно, что представить последовательность в виде программы (иными словами, сжать ее) можно только в том случае, если она содержит какие-то частотные или иные закономерности. Если же их нет, то не существует и программы, более короткой, чем сама последовательность. Отсутствие закономерностей означает случайность в чередовании букв алфавита. Следовательно, можно утверждать, что все последовательности, для которых К_ l(х) - случайны.

3. В связи с этим рассмотрим еще одно свойство алгоритмической сложности. Возьмем множество всех двоичных последовательностей длины N. Тогда общее количество их будет 2^N. Представляет интерес вопрос, какова доля последовательностей, которые могут быть представлены своими программами р так, что l(p) < N. Иначе говоря, какова доля всех сжимаемых последовательностей.

Если последовательность сжата до одного двоичного разряда, то число всех программ такой длины будет 2¹ (ясно, что речь идет о тривиальных рядах нулей или единиц). При сжатии последовательности до 2,3..... к бит число соответствующих программ будет не более 2²,2³,.....2^к . Общее их число, соответственно, составит

Таким образом, доля последовательностей, допускающих сжатие до k бит, будет

при N>>1

Например, при k=10 лишь одна из 2¹⁰=1024 последовательностей допускает сжатие до 10 бит. Следовательно, подавляющее число последовательностей ("почти все") несжимаемы, т.е. случайны.

1.2.4. Наконец, возникает естественный вопрос о способе вычисления алгоритмической сложности. Оказывается, что функция K_ невычислима, т.е. не существует алгоритма ее определения для произвольной символьной последовательности [1], однако существует общий способ сколь угодно хорошей оценки этой величины сверху. Рассмотрим это свойство К_ подробно.

Пусть S - количество символов в алфавите, а N - общее их число в некоторой произвольной последовательности, причем символ с номером i (i=1,2,...s) появляется в ней m_i раз, так что

m₁ + m₂ +.......+m_s = N

Тогда число всевозможных последовательностей будет

Для того, чтобы задать порядковый номер каждый из них в двоичной системе счисления, необходимо logС(m₁, m_2, .....m_s) двоичных разрядов. Воспользовавшись формулой Стирлинга

     lnn!  nlnn - n,

где n - произвольное целое число, получим

EMBED Equation.3

Заметив, что

последнее равенство перепишем в виде

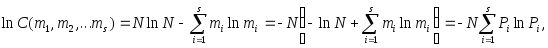
или, в двоичной системе счисления

бит

(здесь- модуль перехода от натуральных логарифмов к двоичным).

Ясно, что в соответствии со свойством 1.2.1. алгоритмическая сложность любой из этих последовательностей не может превосходить количества двоичных разрядов, необходимых для записи их порядковых номеров. Таким образом, имеет место неравенство

,

правая часть которого есть не что иное, как энтропия произвольной последовательности длины N (обычно обозначается буквой Н).

Итак, алгоритмическая сложность любой последовательности не превосходит ее энтропии. Последнюю, как видно из формулы, нетрудно найти, определив частоты (вероятности)

; ; ......

символов в последовательности. Представляется весьма желательным эту верхнюю, "завышенную" оценку алгоритмической сложности уточнить. Поставим следующий вопрос. При какой величине алфавита s максимум энтропии произвольной последовательности из N символов минимален? Иначе говоря, нас интересует минимаксное значение выражения

.

Известно, что Н имеет максимум, когда все (все символы в последовательности равновероятны), и равен, как нетрудно видеть

.

C другой стороны, N не может быть меньше s, так как каждый символ алфавита должен появиться в последовательности хотя бы один раз. Значит, наименьшее (не минимальное!) значение энтропии будет s logs. Таким образом, вопрос состоит в том, что бы найти s, при котором приращение энтропии Н

Н=Нmax - slogs = Nlogs - slogs

было бы минимально ( нужно иметь ввиду, что N может расти неограниченно).Это элементарная задача на экстремум. Решив уравнение

,

получим соотношение между величиной алфавита и длиной последовательности N  slogs, при котором максимум энтропии минимален. Подставив это значение в Hmax, получим

minHmax = slog²s.

Следовательно, уточненное неравенство для алгоритмической сложности произвольной последовательности будет

K_slog²s.