Министерство образования РФ

СПб Государственный электротехнический университет "ЛЭТИ"

Кафедра МО ЭВМ

1. Обзорная лекция

по дисциплине “Метрология программного обеспечения”

на тему

"Математические модели и методы повышения надежности ПО"

Доцент каф. МОЭВМ Кирьянчиков Владимир Андреевич

3. Санкт-Петербург

2001

1. Введение

Степень надежности ПО может быть оценена при помощи некоторых метрик. Модели надежности ПО служат для предсказания значений этих метрик, и кроме того, они позволяют оценить надежность на различных этапах тестирования программного продукта. Например, в том случае, если к некоторому моменту тестирования количество обнаруженных и исправленных ошибок уже достаточно велико, это может создать впечатление, что тестирование продукта близится к завершению, то есть ошибок в программе осталось немного. Однако, это может совершенно не соответствовать действительности, и как раз использование моделей надежности программ может помочь прояснить подобную ситуацию.

2. Основные показатели надежности по

Пусть P(t) - вероятность того, что ни одной ошибки не будет обнаружено на временном интервале [0,t]. Тогда вероятность хотя бы одного отказа за этот период будет Q(t) = 1 – P(t), и плотность вероятности отказов можно записать как

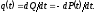
Рассмотрим функцию риска R(t), как условную плотность вероятности отказа программы в момент времени t, при условии, что до этого момента отказов не было:

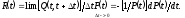(2.1)

Функция риска имеет размерность [1/время]. Из выражения (2.1), ясно, что 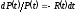, и, следовательно,

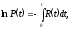
или

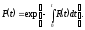(2.2)

Равенство (2.2) является одним из самых важных в теории надежности. Различные виды поведения функции риска во времени порождают различные модели надежности ПО. Интенсивность обнаружения ошибок (функция риска), вместе с вероятностью безотказной работы программы и количеством оставшихся в программе ошибок, являются важнейшими показателями надежности программ.

Прогон программы – это набор действий, включающий в себя: ввод в программу одной из возможных комбинаций E_i пространства входных данных E (); выполнение программы, которое заканчивается либо получением результата F(E_i), либо отказом.

Для некоторых наборов входных данных E_i, отклонение полученного на выходе результата (F’(E_i)) от требуемого результата F(E_i) находится в пределах допустимого отклонения 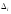, то есть выполняется следующее неравенство:

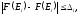
а для всех остальных E_i из подмножества 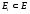, выполнение программы не дает приемлемого результата, то есть

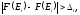
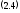
Случаи, описанные неравенством (2.4), называются отказами программы.

Рассмотрим бинарную переменную :

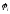Тогда статистическая оценка вероятности отказа программы в течении m прогонов будет равна:

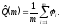
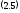
3. Модели, основанные на использовании функции риска

3.1. Модель Джелинского-Моранды.

Это одна из первых и простейших моделей классического типа, послужившая основой для дальнейших разработок в этом направлении. Модель была использована при разработке таких значительных программных проектов, как программа Аполло (некоторых ее модулей). Модель Джелинского-Моранды основана на следующих предположениях:

1. Интенсивность обнаружения ошибок R(t) пропорциональна текущему количеству ошибок в программе, то есть изначальному количеству ошибок за вычетом количества ошибок , уже обнаруженных на данный момент.

2. Все ошибки в программе равновероятны и не зависят друг от друга.

3. Все ошибки имеют одинаковую степень важности.

4. Время до следующего отказа программы распределено экспоненциально.

5. Исправление ошибок происходит без внесения в программу новых ошибок.

6. R(t) = const в промежутке между любыми двумя соседними моментами обнаружения ошибок.

Согласно этим предположениям, функция риска будет представлена как:

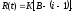
В этой формуле t – это произвольный момент времени между обнаружением (i-1)-й и i-й ошибок; K – неизвестный коэффициент масштабирования; B – начальное количество оставшихся в программе ошибок (также неизвестное).

Таким образом, если в течении времени t было обнаружено (i-1) ошибок, это означает, что в программе еще остается B-(i-1) необнаруженных ошибок.

Полагая, что

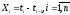
и используя предпосылку 6, а также равенство (2.2), можно заключить, что все X_i имеют экспоненциальное распределение:

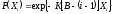
и плотность вероятности отказа, соответственно, равна:

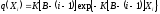
Тогда функцию правдоподобия (согласно предпосылке 2) можно записать как

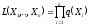
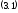
или, переходя к логарифму функции правдоподобия, имеем:

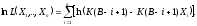(3.2)

Максимум функции правдоподобия можно найти, используя следующие условия:

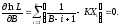(3.3)

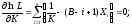(3.4)

Из формулы (3.3) получается оценка максимального правдоподобия для K:

(3.5)

Подставляя выражение (3.5) в (3.4), находим нелинейное уравнение для вычисления 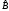–оценки максимального правдоподобия для B:

(3.6)

Это уравнение можно упростить перед тем, как искать его решение, если записать его с использованием следующих обозначений:

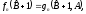(3.7)

где

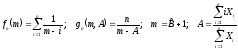
Поскольку имеют смысл лишь целочисленные значения 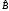, функции из выражения (3.7) можно рассматривать только для целочисленных аргументов. Более того,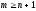, поскольку n ошибок с программе уже обнаружено. Таким образом, оценка максимального правдоподобия для B может быть получена с помощью вычисления начальных значений функций f_n(m) и g_n(m) для m=n+1, n+2…, и анализа разницы |f_n(m)-g_n(m)|.

Поскольку правая и левая части выражения (3.7) одинаково монотонны, это порождает проблему единственности решения, а также проблему его существования. Конечное решение 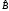в областисуществует тогда и только тогда, когда выполняется неравенство:

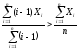(3.8)

В противном случае оценка максимального правдоподобия будет Условие (3.8) можно переписать в более удобном виде:

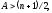(3.9)

где A – то же самое выражение, что и в формуле (3.7). Необходимо отметить, что, A является интегральной характеристикой n встретившихся в программе за время тестирования ошибок, и представляет (в статистическом смысле) набор интервалов X_i между ошибками.

Рассмотрим пример использования модели Джелинского-Моранды, в котором она применяется к следующим экспериментальным данным: в течение 250 дней было обнаружено 26 ошибок, интервалы между обнаружением которых представлены в таблице 3.1. Для этих данных мы имеем n=26 и 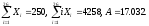. Условие (3.9) выполняется, и, таким образом, оценка максимального правдоподобия имеет единственное решение. В таблице 3.2 представлены начальные значения функций, входящих в уравнение (3.7), для множества аргументов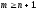

Наилучшим решением для уравнения (3.7) является m=32 (соответствующая строка в таблице дает минимальное значение разницы функций по модулю, то есть максимально приближает ее к нулю, что нам и требуется), то есть 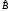= m-1=31. Из выражения (3.5) находим = 0.007.

Среднее время 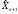(время, оставшееся до обнаружения (n+1)-й ошибки) есть инвертированная оценка интенсивности для предыдущей ошибки:

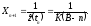
В этом примере, 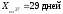, и время до полного завершения тестирования

Таблица 3.1. Интервалы между обнаружением ошибок.

I	Xi	i	Xi	i	Xi	i	Xi
1	9	8	8	15	4	21	11
2	12	9	5	16	1	22	33
3	11	10	7	17	3	23	7
4	4	11	1	18	3	24	91
5	7	12	6	19	6	25	2
6	2	13	1	20	1	26	1
7	5	14	9

Таблица 3.2. Значения функций.

m
27	3.854	2.608	1.246
28	2.891	2.371	0.520
29	2.427	2.172	0.255
30	2.128	2.005	0.123
31	1.912	1.861	0.051
32	1.744	1.737	0.007
33	1.608	1.628	-0.020
34	1.496	1.532	-0.036