Impinvar – метод инвариантной импульсной характеристики для перевода аналогового фильтра в цифровой:
[BZ,AZ] = IMPINVAR(B,A,Fs) создает цифровой фильтр с коэффициентами числителя и знаменателя BZ и AZ соответственно, чей импульсный отклик эквивалентен импульсному отклику аналогового фильтра с коэффициентами B и A при частоте дискретизации Fs (в герцах).
Если Fs не определено, то по умолчанию равно 1 Гц.
Смотри также BILINEAR.
8. Примеры проектирования цифровых фильтров
8.1. Генерация входной последовательности сигнала
В примере используется входная последовательность x полигармонического сигнала с частотами F1 = 3 Гц, F2 =7 Гц, F3 =25 Гц, частота дискретизации Fs=128 Гц, время наблюдения T = 4 c.
T = 4; % время реализации
Fs = 128; % частота дискретизации
n = T *Fs; % длина реализации
t = (0:n-1)/Fs; % шаг дискретизации
indx = (0:n-1)'; % вектор целых чисел 512
Генерация полигармоническиого сигнала: ai cos (wit), wi = 3, 7, 10, 25 Гц:
format short
w1 = 3;
w2 = 7;
w3 = 10;
w4 = 25;
x = 30*cos(w1*2*pi*t) + 60*cos(w2*2*pi*t) + 90*cos(w3*2*pi*t) + 30*cos(w4*2*pi*t);
Построение графика входной последовательности (рис. 8.1):
clf, plot(t,x)
ylabel('Amplitude (mkV)')
xlabel('Time')
title('Input sequence')
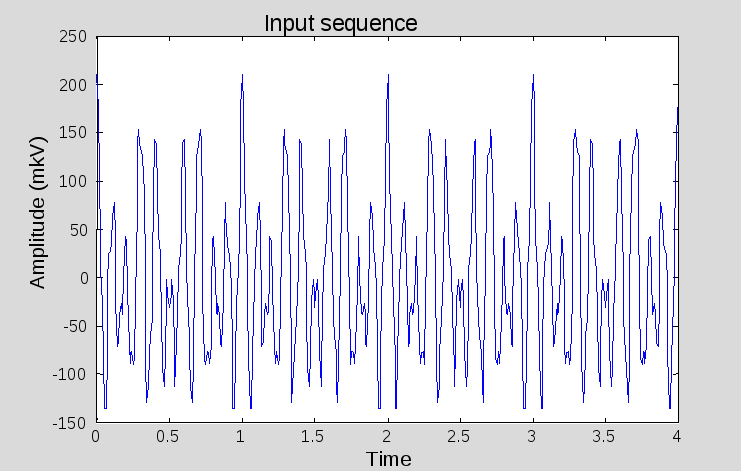
Рис. 8.1
На 8.1 показан график входной последовательности полигармонического сигнала.
8.2. Реализация спектрального анализа с использованием бпф
Следующий листинг иллюстрирует вычисление прямого дискретного преобразования Фурье для взвешенной с помощью окна реализации сигнала с использованием функций одномерного преобразования FFT, построение графика модуля спектральной функции (рис. 8.2):
format long e
FT=fft(bartlett(n).*x');
FT=FT(1:n/2);
step = indx(1:(n/2))*(1/T); % разрешение FFT
clf, plot(step,abs(FT),'b')
axis([0 35 0 max(abs(FT))]);
grid on
ylabel('Magnitude')
xlabel('Frequency (Hertz)')
title('Power spectrum')
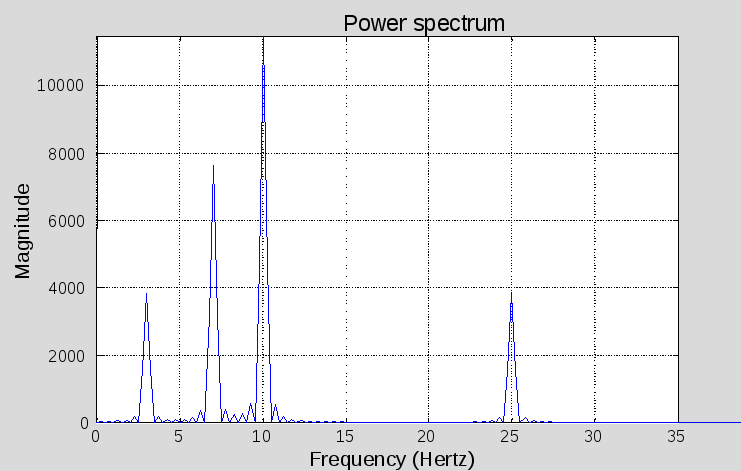
Рис. 8.2
На рисунке 8.2. приведена амплитудно-частотная характеристика входного сигнала.
8.3. Синтез цифрового ких-фильтра
Приводится пример синтеза низкочастотного КИХ-фильтра с использованием окон Хэмминга (амплитудно-частотная характеристика (АХЧ) показана на рис. 8.3) и Бартлетта (АЧХ изображена на рис. 8.4).
Wn = (13/Fs)*2; % частота среза
len = 21; % длина фильтра
b = FIR1(len, Wn); % проектирование НЧ–фильтра
% с окном Хэмминга
[H,F] = freqz(b,1,n,Fs);
clf, plot (F,abs(H));
ylabel('Magnitude')
xlabel('Frequency (Hertz) ')
title('Filter Response')
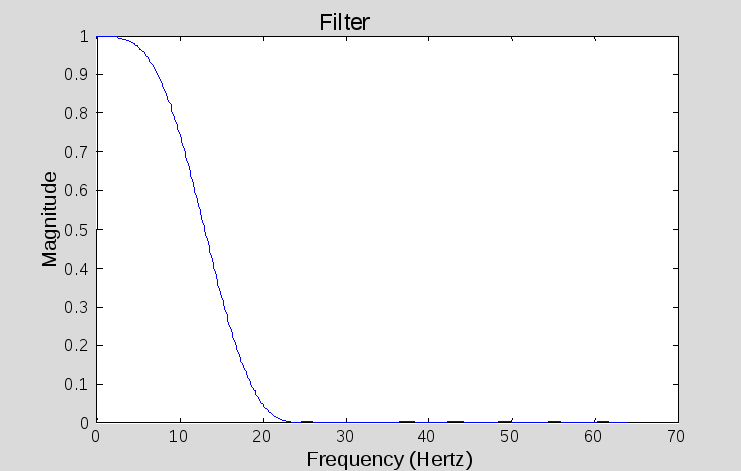
Рис. 8.3
Wn = (13/Fs)*2; % частота среза
len = 21; % длина фильтра
% проектирование фильтра с окном Бартлетта
b = FIR1(len,Wn,bartlett(len+1));
[H,F] = freqz(b,1,n,Fs);
clf, plot (F,abs(H));
ylabel('Magnitude')
xlabel('Frequency (Hertz) ')
title('Filter Response')
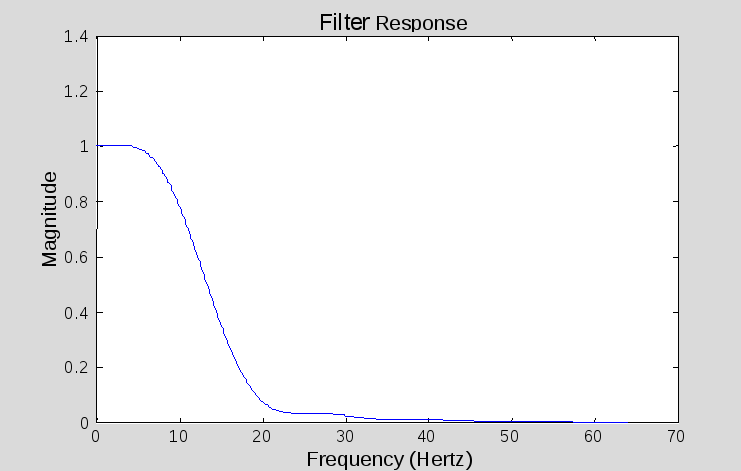
Рис. 8.4
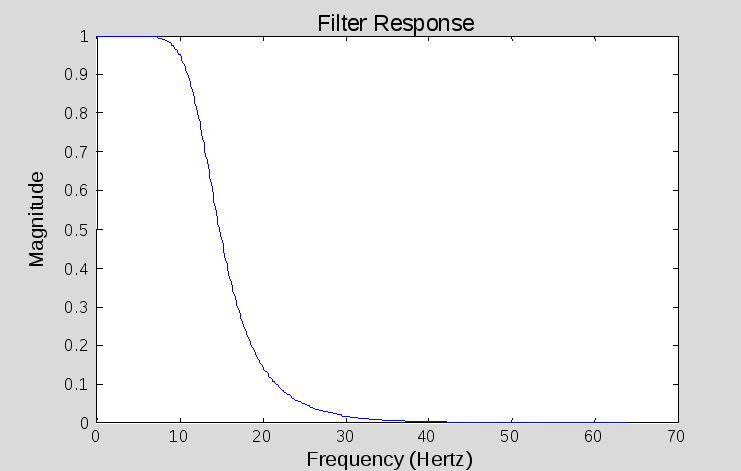
Рис. 8.5
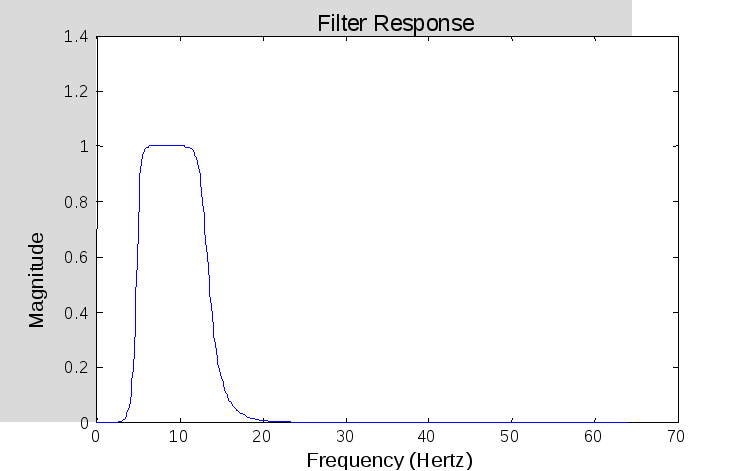
Рис.8.6
Далее рассмотрен пример синтеза цифровых БИХ–фильтров Баттерворта. АЧХ НЧ–фильтра приведена на рис. 8.5. На рис. 8.6 приводится АЧХ для полосового фильтра.
Wn = (13/Fs)*2;
[b,a] = BUTTER(4,Wn); % проектирование НЧФ
[H,F] = freqz(b,a,n,Fs);
clf,plot (F,abs(H));
ylabel('Magnitude')
xlabel('Frequency (Hertz) ')
title('Filter Response')
Wn = [(5/Fs)*2 (13/Fs)*2];
[b,a] = BUTTER(6,Wn);
% проектирование полосового фильтра
[H,F] = freqz(b,a,n,Fs);
clf,plot (F,abs(H));
ylabel('Magnitude')
xlabel('Frequency (Hertz) ')
title('Filter Response')