
- •1. Общая характеристика цифровых фильтров
- •1.1. Свойства цифровых фильтров
- •1.2. Представление цифрового фильтра в виде разностного уравнения
- •2. Ких-фильтры. Методы синтеза
- •2.1. Прямоугольное окно
- •2.2. Обобщенное окно Хэмминга
- •2.3. Окно Блэкмана
- •2.4. Окно Кайзера
- •3. Бих-фильтры. Методы синтеза
- •3.1. Аналоговые фильтры-прототипы
- •3.1.1. Фильтры Баттерворта
- •3.1.2. Фильтры Чебышева
- •3.1.3. Эллиптические фильтры
- •3.1.4. Фильтры Бесселя
- •3.2. Методы дискретизации аналогового фильтра
- •3.2.1. Метод инвариантного преобразования импульсной характеристики
- •3.2.2. Метод билинейного преобразования
- •3.3. Преобразования полосы частот для аналоговых фильтров
- •3.4. Преобразование полосы для цифровых фильтров
- •4. Методы реализации цифровых фильтров
- •4.1. Прямая форма
- •4.2. Прямая каноническая форма
- •4.3. Каскадная форма
- •4.4. Параллельная форма
- •5. Работа в среде matlab
- •5.1. Ввод матриц
- •5.2. Матричные операции
- •5.3. Операторы, выражения и переменные
- •5.4. Функции построения матриц
- •5.5. Операторы for, while, if
- •5.6. Скалярные функции
- •5.7. Векторные функции
- •5.8. Mатричные функции
- •5.9. Подматрицы и форма записи с двоеточием
- •5.10. M-файлы
- •5.11. Текстовые строки, сообщения об ошибках, ввод данных
- •5.12. Сравнение эффективности алгоритмов
- •5.13. Формат вывода
- •5.14. Протокол
- •5.15. Графика
- •6. Записная книжка matlab для Microsoft Word
- •6.1. Начало работы
- •6.2. Краткий пример использования Записной книжки
- •7. Проектирование цифровых фильтров в среде matlab
- •Filtic – cоздание начального состояния для функции filter:
- •Freqs – частотная характеристика аналогового фильтра:
- •Freqspace – формирование последовательности отсчетов частоты:
- •Freqz – частотная характеристика цифрового фильтра.
- •Grpdelay – групповая задержка цифрового фильтра:
- •Impz – импульсный отклик цифрового фильтра:
- •Unwrap – корректировка фазовых углов:
- •Zplane – отображение нулей и полюсов цифрового фильтра:
- •7.2. Проектирование цифровых бих-фильтров besself – проектирование аналогового фильтра Бесселя:
- •Butter – проектирование цифрового и аналогового фильтров Баттерворта:
- •Cheby1 – проектирование цифрового и аналогового фильтров Чебышева – первого типа:
- •Cheby2 – проектирование цифрового и аналогового фильтров Чебышева второго типа:
- •Ellip – проектирование эллиптического цифрового и аналогового фильтров:
- •Yulewalk – проектирование рекурсивного фильтра с использованием метода наименьших квадратов по заданной амплитудно-частотной характеристике:
- •7.3. Выбор порядка бих-фильтра buttord – выбор порядка фильтра Баттерворта:
- •Cheb1ord – выбор порядка для фильтра Чебышева первого порядка:
- •Cheb2ord– выбор порядка для фильтра Чебышева первого порядка:
- •Ellipord – выбор порядка эллиптического фильтра:
- •7.4. Проектирование ких-фильтров fir1 – фильтр fir проектируется с использованием метода окна:
- •Fir2– проектирование фильтра fir с использованием оконного метода для произвольной формы фильтра:
- •Firls – проектирование ких-фильтра с использованием минимизации ошибок методом наименьших квадратов (мнк):
- •Intfilt – расчет интерполирующего ких-фильтра:
- •Remez – синтез оптимального fir-фильтра с равномерной (чебышевской) аппроксимацией на основе алгоритма Паркса – Мак-Клелана:
- •7.5. Преобразования czt–z-преобразование по спиральному контуру:
- •Dct– дискретное косинусное преобразование:
- •Impinvar – метод инвариантной импульсной характеристики для перевода аналогового фильтра в цифровой:
- •8. Примеры проектирования цифровых фильтров
- •8.1. Генерация входной последовательности сигнала
- •8.2. Реализация спектрального анализа с использованием бпф
- •8.3. Синтез цифрового ких-фильтра
- •8.4. Реализация цифровой фильтрации
- •Список литературы
- •Содержание
- •197376, С.-Петербург, ул. Проф. Попова, 5
3.1. Аналоговые фильтры-прототипы
Приведем расчетные формулы для нескольких стандартных типов аналоговых фильтров. Допустим, нужно рассчитать аналоговый фильтр нижних частот с частотой среза W = 1 рад/с. В качестве аппроксимируемой функции будет использоваться квадрат амплитудной характеристики (исключением является фильтр Бесселя).
Будем считать, что передаточная функция аналогового фильтра является рациональной функцией переменной s следующего вида:
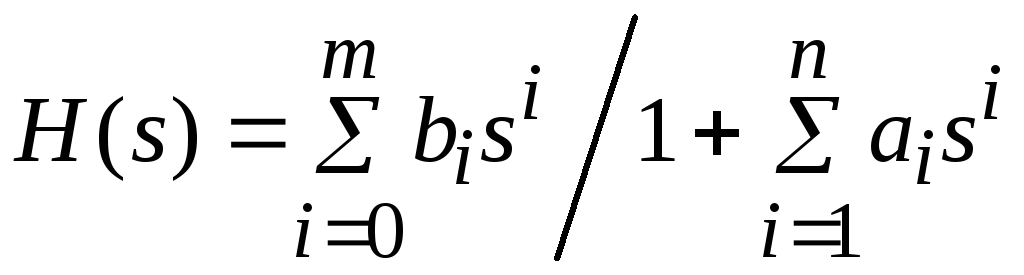 .
.
3.1.1. Фильтры Баттерворта
Фильтры Баттерворта нижних частот характеризуются тем, что имеют максимально гладкую амплитудную характеристику в начале координат в s-плоскости. Квадрат амплитудной характеристики нормированного (т. е. имеющего частоту среза 1 рад/с) фильтра Баттерворта равен
![]() ,
,
где n – порядок фильтра. Аналитически продолжая функцию на всю s-плоскость, получим:
![]()
Все полюсы этой функции находятся на единичной окружности на одинаковом расстоянии друг от друга в s-плоскости. Выразим передаточную функцию H(s) через полюсы, располагающиеся в левой полуплоскости s:
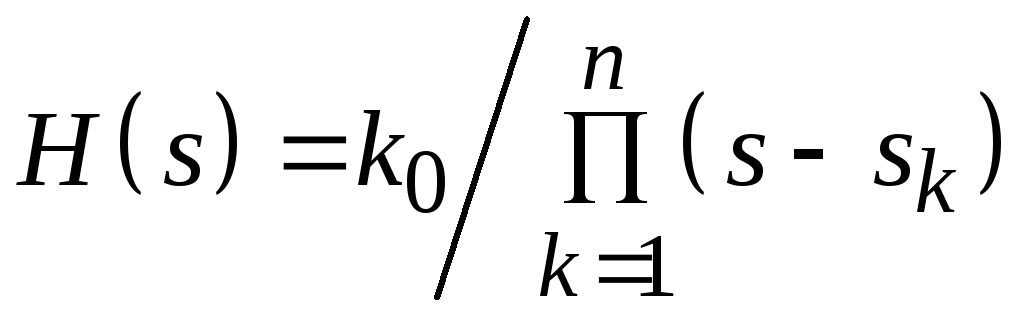 ,
,
где
![]() ,k
= 1, 2, ..., n;
k0
– константа нормирования.
,k
= 1, 2, ..., n;
k0
– константа нормирования.
Можно сформулировать несколько свойств фильтров Баттерворта нижних частот:
Фильтры Баттерворта имеют только полюсы (все нули передаточных функций этих фильтров расположены на бесконечности).
На частоте W= 1 рад/с коэффициент передачи фильтра равен
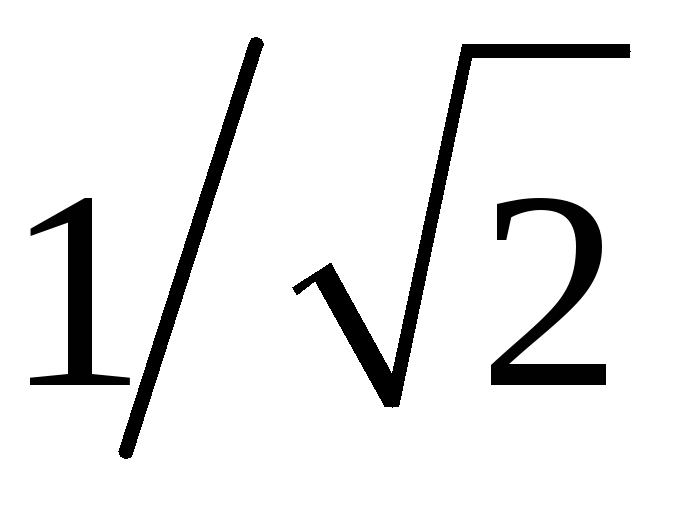 (т. е. на частоте среза
их амплитудная характеристика снижается
на 3 дБ).
(т. е. на частоте среза
их амплитудная характеристика снижается
на 3 дБ).Порядок фильтра nполностью определяет весь фильтр.
3.1.2. Фильтры Чебышева
Отличительной чертой фильтров Чебышева является наименьшая величина максимальной ошибки аппроксимации в заданной полосе частот. В действительности ошибка аппроксимации представляется в заданной полосе частот равновеликими пульсациями, т. е. она флуктуирует между максимумами и минимумами равной величины. В зависимости от того, где минимизируется ошибка аппроксимации – в полосе пропускания или в полосе непропускания, – различают фильтры Чебышева типа 1 и 2.
Фильтры Чебышева типа 1 имеют только полюсы и обеспечивают равновеликие пульсации амплитудной характеристики в полосе пропускания и монотонное изменение ослабления в полосе непропускания. Квадрат амплитудной характеристики фильтра Чебышева типа 1 n-го порядка описывается выражением
![]() ,
,
где
![]() – полином Чебышеваn-го
порядка, по определению равный
– полином Чебышеваn-го
порядка, по определению равный
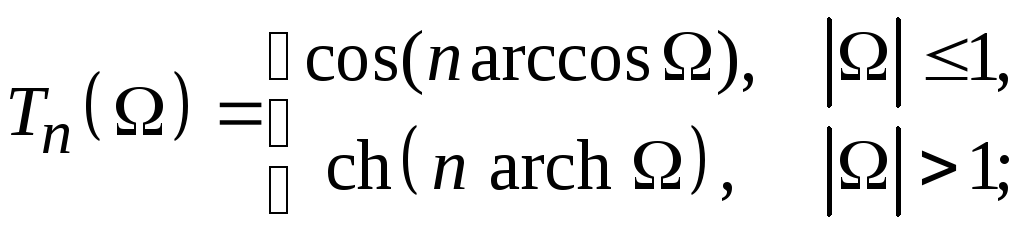
e – параметр, характеризующий пульсации в полосе пропускания.
Свойство оптимальности фильтров Чебышева типа 1 порядка n заключается в том, что не существует какого-либо другого фильтра n-го порядка, содержащего только полюсы, который имел бы такие же или лучшие характеристики и в полосе пропускания, и в полосе непропускания.
Фильтры Чебышева типа 2 (иногда их называют обратными фильтрами Чебышева) обеспечивают монотонное изменение ослабления в полосе пропускания и равновеликие пульсации в полосе непропускания. Нули фильтров этого типа располагаются на мнимой оси в s-плоскости, а полюсы – в левой полуплоскости. Квадрат амплитудной характеристики фильтров Чебышева типа 2 порядка n можно представить следующим образом:
![]() ,
,
где Wr – наинизшая частота, на которой в полосе непропускания достигается заданный уровень ослабления.
