
- •1. Общая характеристика цифровых фильтров
- •1.1. Свойства цифровых фильтров
- •1.2. Представление цифрового фильтра в виде разностного уравнения
- •2. Ких-фильтры. Методы синтеза
- •2.1. Прямоугольное окно
- •2.2. Обобщенное окно Хэмминга
- •2.3. Окно Блэкмана
- •2.4. Окно Кайзера
- •3. Бих-фильтры. Методы синтеза
- •3.1. Аналоговые фильтры-прототипы
- •3.1.1. Фильтры Баттерворта
- •3.1.2. Фильтры Чебышева
- •3.1.3. Эллиптические фильтры
- •3.1.4. Фильтры Бесселя
- •3.2. Методы дискретизации аналогового фильтра
- •3.2.1. Метод инвариантного преобразования импульсной характеристики
- •3.2.2. Метод билинейного преобразования
- •3.3. Преобразования полосы частот для аналоговых фильтров
- •3.4. Преобразование полосы для цифровых фильтров
- •4. Методы реализации цифровых фильтров
- •4.1. Прямая форма
- •4.2. Прямая каноническая форма
- •4.3. Каскадная форма
- •4.4. Параллельная форма
- •5. Работа в среде matlab
- •5.1. Ввод матриц
- •5.2. Матричные операции
- •5.3. Операторы, выражения и переменные
- •5.4. Функции построения матриц
- •5.5. Операторы for, while, if
- •5.6. Скалярные функции
- •5.7. Векторные функции
- •5.8. Mатричные функции
- •5.9. Подматрицы и форма записи с двоеточием
- •5.10. M-файлы
- •5.11. Текстовые строки, сообщения об ошибках, ввод данных
- •5.12. Сравнение эффективности алгоритмов
- •5.13. Формат вывода
- •5.14. Протокол
- •5.15. Графика
- •6. Записная книжка matlab для Microsoft Word
- •6.1. Начало работы
- •6.2. Краткий пример использования Записной книжки
- •7. Проектирование цифровых фильтров в среде matlab
- •Filtic – cоздание начального состояния для функции filter:
- •Freqs – частотная характеристика аналогового фильтра:
- •Freqspace – формирование последовательности отсчетов частоты:
- •Freqz – частотная характеристика цифрового фильтра.
- •Grpdelay – групповая задержка цифрового фильтра:
- •Impz – импульсный отклик цифрового фильтра:
- •Unwrap – корректировка фазовых углов:
- •Zplane – отображение нулей и полюсов цифрового фильтра:
- •7.2. Проектирование цифровых бих-фильтров besself – проектирование аналогового фильтра Бесселя:
- •Butter – проектирование цифрового и аналогового фильтров Баттерворта:
- •Cheby1 – проектирование цифрового и аналогового фильтров Чебышева – первого типа:
- •Cheby2 – проектирование цифрового и аналогового фильтров Чебышева второго типа:
- •Ellip – проектирование эллиптического цифрового и аналогового фильтров:
- •Yulewalk – проектирование рекурсивного фильтра с использованием метода наименьших квадратов по заданной амплитудно-частотной характеристике:
- •7.3. Выбор порядка бих-фильтра buttord – выбор порядка фильтра Баттерворта:
- •Cheb1ord – выбор порядка для фильтра Чебышева первого порядка:
- •Cheb2ord– выбор порядка для фильтра Чебышева первого порядка:
- •Ellipord – выбор порядка эллиптического фильтра:
- •7.4. Проектирование ких-фильтров fir1 – фильтр fir проектируется с использованием метода окна:
- •Fir2– проектирование фильтра fir с использованием оконного метода для произвольной формы фильтра:
- •Firls – проектирование ких-фильтра с использованием минимизации ошибок методом наименьших квадратов (мнк):
- •Intfilt – расчет интерполирующего ких-фильтра:
- •Remez – синтез оптимального fir-фильтра с равномерной (чебышевской) аппроксимацией на основе алгоритма Паркса – Мак-Клелана:
- •7.5. Преобразования czt–z-преобразование по спиральному контуру:
- •Dct– дискретное косинусное преобразование:
- •Impinvar – метод инвариантной импульсной характеристики для перевода аналогового фильтра в цифровой:
- •8. Примеры проектирования цифровых фильтров
- •8.1. Генерация входной последовательности сигнала
- •8.2. Реализация спектрального анализа с использованием бпф
- •8.3. Синтез цифрового ких-фильтра
- •8.4. Реализация цифровой фильтрации
- •Список литературы
- •Содержание
- •197376, С.-Петербург, ул. Проф. Попова, 5
4.3. Каскадная форма
Записав формулу (4.1) в виде
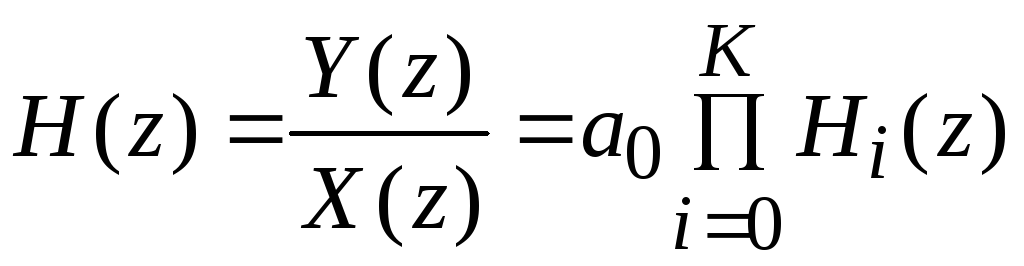 , (4.2)
, (4.2)
получим третью структуру построения цифрового фильтра. Множители Hi(z) соответствуют либо блокам второго порядка, т. е.
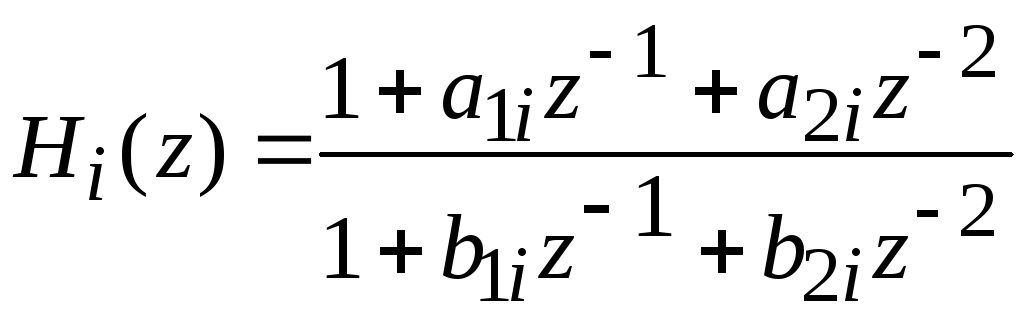 ,
,
либо блокам первого порядка, т. е.
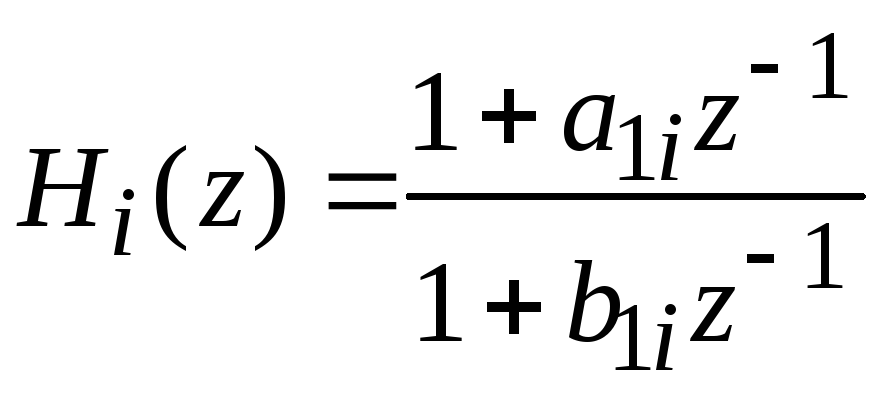 ,
,
а K равно
целой части числа
![]() .
Схему, реализующую формулу (4.2), называют
каскадной (или последовательной) формой
(рис. 4.4).
.
Схему, реализующую формулу (4.2), называют
каскадной (или последовательной) формой
(рис. 4.4).
![]()
Рис. 4.4
Каждый из блоков, образующих последовательную форму, можно реализовать в прямой или канонической форме.
4.4. Параллельная форма
Другим способом описания передаточной функции может быть ее представление разложением на простые дроби:
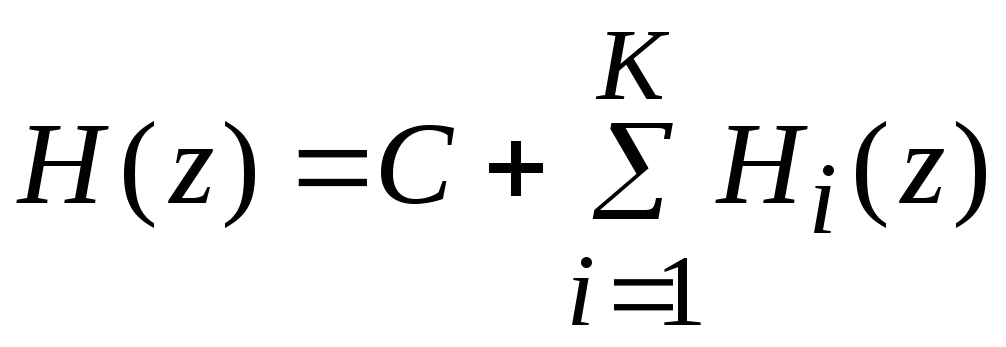 , (4.3)
, (4.3)
где слагаемые Hi(z) соответствуют или блокам второго порядка:
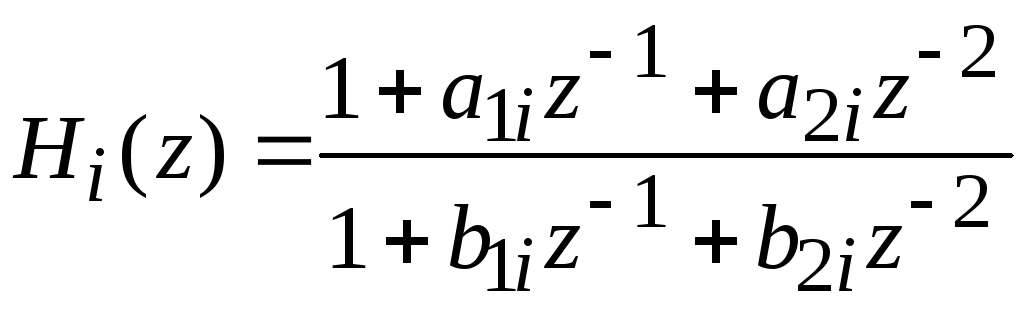 ,
,
или блокам первого порядка:
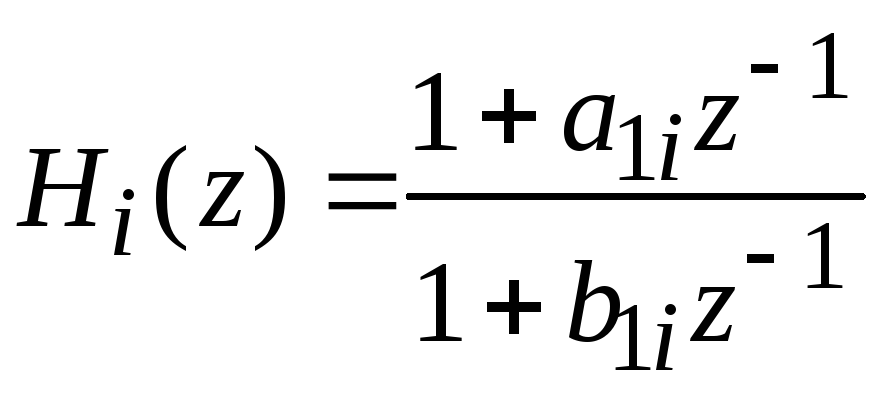 ,
,
причем К
равно целой части от
![]() и
и![]() .
.
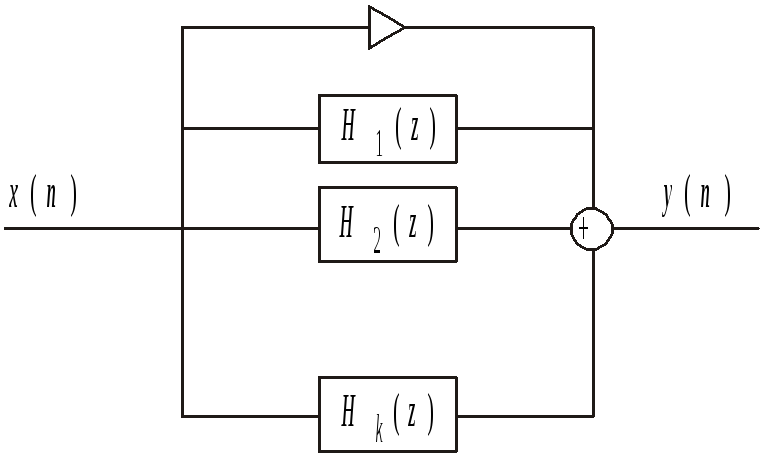
Рис. 4.5
На рис. 4.5 приведена структурная схема, реализующая соотношение (4.3). Ее называют параллельной формой. Блоки 1-го и 2-го порядка строятся по схеме одной из прямых форм.
5. Работа в среде matlab
MATLAB (сокращение от MATrix LABoratory – "матричная лаборатория") – это интерактивная матрично-ориентированная система для научных и инженерных расчетов. MATLAB дает возможность решать сложные численные задачи без непосредственного написания программ.
Изложенный материал предназначен для начинающих пользователей MATLAB. Для получения детальной информации о функциях системы используйте системную помощь (команда help). После входа в MATLAB команда help вызовет появление списка функций, о которых можно получить информацию; команда help <имя функции> даст сведения об этой функции. Вы можете получить представление о некоторых возможностях MATLAB при помощи команды demo.
5.1. Ввод матриц
Основной тип объектов, с которыми оперирует MATLAB, – это прямоугольные матрицы с возможными комплексными элементами. Матрицы 11 интерпретируются как скаляры, а матрицы-столбцы и матрицы-строки – как векторы.
Ввести матрицу можно следующими способами:
ввести полный список элементов;
сгенерировать с помощью встроенной функции;
создать в М-файле (см. 5.13);
загрузить из внешнего файла данных.
Например, операторы А
= [1 2 3; 4 5 6; 7 8 9] и А
=
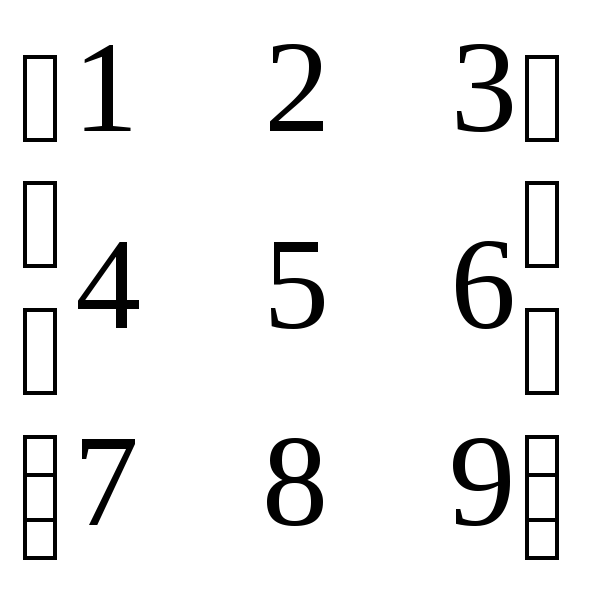 создают матрицуА(3, 3).
создают матрицуА(3, 3).
Элементы строки матрицы разделяются запятыми или пробелами. Числа в экспоненциальной форме вводятся без пробелов (например, 2.39е-4). Ввод больших матриц лучше осуществлять в М-файлах, где проще исправить ошибки ввода (см. 5.8).
Встроенные функции rand, magic и hilb позволяют создавать матрицы для экспериментов. Команда rand(n) или rand(n, m) генерирует матрицу размером nn или nm с равномерно распределенными элементами; magic(n) (магический квадрат) генерирует целочисленную матрицу, у которой сумма элементов строк равна сумме элементов столбцов; hilb(n) создает гильбертову матрицу размером nn, важнейшую среди плохообусловленных матриц. Матрицы также могут быть сгенерированы циклом for (см. 5.6).
К отдельным элементам матриц и векторов можно обращаться при помощи индексов, заключенных в круглые скобки. Например А(2, 3) – элемент 2-й строки 3-го столбца матрицы А.
5.2. Матричные операции
К матрицам можно применять следующие матричные операции:
+– сложение;
– – вычитание;
– умножение;
^– возведение в степень;
'– транспонирование;
\– левое деление;
/– правое деление.
Эти операции можно применять и к скалярам (матрицам 11). Если размеры матриц несовместимы при данной матричной операции, то будет выдано сообщение об ошибке, (за исключением случая скалярно-матричных операций). Матричное деление заслуживает особого комментария. Если А – обратимая квадратная матрица, а b – вектор-столбец (cтрока) соответствующей длины, то х = А\b – решение уравнения А*х = b (х = b/A – решение уравнения х*A = b).
В левом делении если А – квадратная, она факторизуется при помощи гауссовского исключения, если же А – не квадратная, то она факторизуется при помощи ортогонализации по Хаусхолдеру с вращением столбца.
Правое деление определяется в терминах левого следующим образом: b/A = (A'\b')'.
Важно заметить, что операции *, ^, /, \ выполняются ПОЭЛЕМЕНТНО, если перед ними поставить точку. Например, [1, 2, 3, 4]*[1, 2, 3, 4] и [1, 2, 3, 4]^2 дадут одинаковый результат [1, 4, 9, 16].
