Дискретное преобразование Фурье

Дискретное преобразование Фурье.

Преобразование Фурье служит для перехода из одной области, в которой мы рассматриваем некоторый объект (как правило это функция, описывающий этот объект), в другую, в которой те или иные свойства объекта могут быть наиболее полно и точно исследованы. Основой для преобразования Фурье является набор (базис) ортогональных функций, по которому производят разложение объекта (функции) в ряд Фурье.

Применительно к исследованию сигналов, преобразование Фурье используют для перехода из временной области в частотную, позволяющего получить частотный спектр сигнала. Суть и основные свойства метода изложены ниже.

Рассмотрим периодическую последовательность с периодом в N отсчетов. Ее можно записать следующим образом

x_p(n)= X_p(k) , (1)

причем частоты спектральных составляющих, образующих x_p(n) , могут принимать только значения _k=2k/N, -<k<, поскольку периоды других частот не кратны N. В равенстве (1) коэффициенты X_p(k) представляют амплитуды синусоид с частотами _k . Запись вида (1) избыточна вследствие периодичности функции , т.к. комплексные экспоненты с частотами _k=2k/N и _kmN=(2/N)(k  mN), -<m<, не отличаются друг от друга, т.е.

= (2)

Следовательно, равенство (1) можно переписать в виде

x_p(n)= X_p(k) (3)

подчеркивающем наличие всего N различных комплексных экспонент с периодом в N отсчетов. Для удобства перепишем равенство (3) в общепринятом виде

x_p(n)= X_p(k) (4)

где деление на N не изменяет способа представления. Чтобы выразить коэффициенты X_p(k) через x_p(n) умножим обе части равенства (4) на и просуммируем результаты по n

(5)

Меняя в правой части (5) порядок умножения и используя формулу

(6)

получим

(7)

или [после перестановки левой и правой частей равенства (7) и замены индекса m на k]

(8)

Соотношение (8) носит название дискретного преобразования Фурье (ДПФ), а (3) – обратного преобразования Фурье (ОДПФ).

Из определений (3) и (8) видно, что обе последовательности x_p(n) и X_p(k) полностью определяются одним периодом x_p(n) . Отсюда возникает интересный вопрос: как связаны z-преобразование конечной последовательности, образованной из одного периода периодической последовательности, и ДПФ всей периодической последовательности? Иначе говоря, рассмотрим последовательность конечной длины

(9)

причем последовательность x_p(n) имеет период в N отсчетов, т.е. x(n) представляет собой один период последовательности x_p(n). z-преобразование x(n) равно

(10)

Вычисляя сумму (10) при z=, т.е. в точке на единичной окружности с полярным углом 2k/N, находим

(11)

Сравнивая суммы (11) и (8) и учитывая, что x_p(n) =x(n) на интервале 0 n  N-1, получаем

(12)

Итак, коэффициенты ДПФ последовательности конечной длины равны значениям z-преобразования этой же последовательности в N точках, равномерно распределенных по единичной окружности. Еще более важный вывод состоит в том, что коэффициенты ДПФ последовательности конечной длины однозначно представляют саму последовательность, т.к. по ним можно точно восстановить исходную последовательность, используя ОДПФ. Итак, хотя ДПФ и ОДПФ вводятся для периодических последовательностей, важно, что через них можно представлять последовательности конечной длины.

Свойства ДПФ.

1. Линейность

Если x_p(n) и y_p(n) – периодические последовательности (с периодом в N отсчетов каждая), а X_p(k) и Y_p(k) – их ДПФ, то дискретное преобразование Фурье последовательности x_p(n)+ y_p(n) равно X_p(k) + Y_p(k). Это положение справедливо и для последовательностей конечной длины.

2. Сдвиг

Если последовательность x_p(n) периодическая с периодом в N отсчетов, а ее ДПФ равно X_p(k), то ДПФ периодической последовательности x_p(n-n₀) будет равно

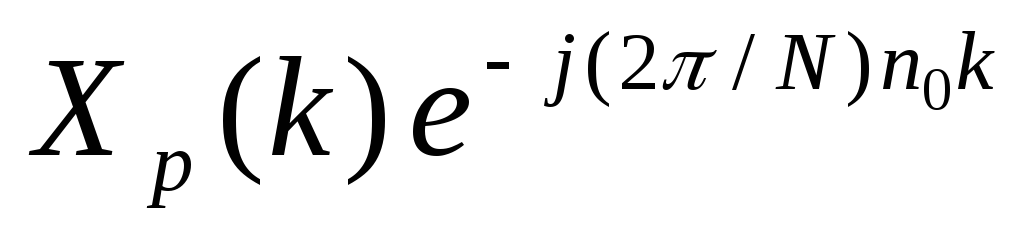
3. Свойства симметрии

Если периодическая последовательность x_p(n) с периодом в N отсчетов является действительной, то ее ДПФ X_p(k) удовлетворяет следующим условиям симметрии

Re[X_p(k)]=Re[X_p(N-k)]

Im[X_p(k)]=-Im[X_p(N-k)]

| X_p(k)|=| X_p(N-k)|

arg X_p(k)=-arg X_p(N-k)

Аналогичные равенства справедливы и для конечной последовательности x(n), имеющей N-точечное ДПФ X(k).

4. Свертка последовательностей

Если x_p(n) и h_p(n) – две периодические последовательности с периодами по N отсчетов и ДПФ, равными

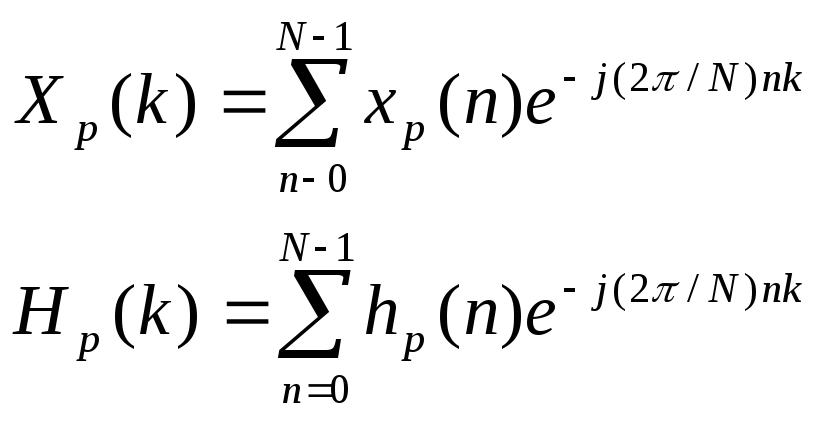
то N-точечное ДПФ последовательности y_p(n) , являющейся круговой (или периодической) сверткой последовательностей x_p(n) и h_p(n), т.е.

,

равно

Y_p(k)=H_p(k)X_p(k)