
6.2. Краткая сводка результатов
Параметрический метод спектрального оценивания состоит из трех этапов. На первом из них производится выбор параметрической модели временного ряда, соответствующий имеющейся записи измеренных данных. В этой главе будут рассмотрены три типа параметрических моделей временных рядов: авторегрессионная (АР) модель, модель скользящего среднего (СС) и комбинированная модель авторегрессии - скользящего среднего (АРСС). На втором этапе вычисляются оценки параметров модели. На третьем этапе оцененные значения параметров вводятся в теоретическое выражение для спектральной плотности мощности, соответствующее избранной модели.
В табл.6.1 указаны номера уравнений для АР-, СС-, и АРСС-моделей, которые приводятся в данной главе. В приложении 6.А помещена машинная программа ARMAPSD, предназначенная для вычисления значений СПМ по заданным значениям параметров соответствующей модели. Выбор одной из трех моделей, приведенных в табл.6.1, требует некоторых предварительных сведений о возможной форме спектральной оценки. Если необходимы спектры с острыми пиками, но без глубоких впадин (нулей), то наиболее подходящей является АР-модель. Если, наоборот, необходимы спектры с глубокими нулями, но без острых пиков, то подойдет СС-модель. Что же касается АРСС-модели, то она может, вообще говоря, применяться в обоих этих предельных случаях. В тех случаях, когда одинаково пригодна любая из трех моделей, следует, по всей вероятности, использовать ту из них, которая имеет наименьшее число параметров. Этот принцип экономии был предложен Боксом и Дженкинсом [1] и основан на том факте, что получить оценки с хорошими статистическими свойствами можно, как правило, тогда, когда число оцениваемых параметров минимально. Заметим, однако, что вычислительные затраты для оценивания параметров АР-модели часто значительно меньше вычислительных затрат, требуемых для оценивания параметров СС- и АРСС-моделей, поэтому АР-модель временного ряда иногда выгодно применять даже тогда, когда она не является моделью с наименьшим числом параметров. Вопросы, касающиеся числа параметров для уже выбранной модели будут рассмотрены в гл.8 и10.
Таблица 6.1. Сводка основных соотношений для параметрических моделей
|
Основные соотношения |
АРСС |
АР |
СС |
|
Определение временного ряда |
(6.1) |
(6.13) |
(6.11) |
|
Автокорреляционная последовательность |
(6.29) |
(6.31) |
(6.35) |
|
СПМ (на основе параметров) |
(6.8) |
(6.14) |
(6.12) |
|
СПМ (на основе АКП) |
- |
(6.33) |
(6.36) |
|
Эквивалентность АР-(¥)-модели |
(6.17) |
- |
(6.17) |
|
Эквивалентность СС-(¥)-модели |
(6.24) |
(6.24) |
- |
6.3. Ар-, сс- и арсс-модели случайных процессов
Модель временного ряда, которая пригодна для аппроксимации многих встречающихся на практике детерминированных и стохастических процессов с дискретным временем, описывается выходом фильтра, выражаемым следующим линейным разностным уравнением с комплексными коэффициентами:
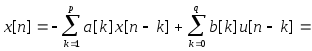 (6.1)
(6.1)
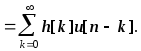 (6.2)
(6.2)
Здесь x[n] - последовательность на выходе казуального фильтра (h[k]=0 при k<0), который формирует наблюдаемые данные, а u[n] - входная возбуждающая последовательность. Без потери общности можно положить b[0]=1, так как вход u[n] всегда можно соответствующим образом промасштабировать, с тем чтобы учесть любой коэффициент усиления фильтра. Выше было показано, что системная функция H(z) , связывающая вход и выход этого фильтра имеет рациональную форму
H(z)
=
![]() (6.3)
(6.3)
в которой полиномы определяются следующими выражениями:
A(z)
= 1 +
![]() (6.4)
(6.4)
B(z)
= 1 +
![]() (6.5)
(6.5)
H(z)
= 1+
![]() (6.6)
(6.6)
При этом предполагается, что нули полиномов A(z) и B(z) расположены внутри единичной окружности в z-плоскости, с тем чтобы гарантировать принадлежность функции H(z) устойчивому минимально-фазовому казуальному фильтру.
Согласно выражениям z-преобразование автокорреляции выходной последовательности x[n] и z-преобразование автокорреляции входного случайного процесса u[n] связаны соотношением
Pxx (z) = Puu (z)H(z)H*(1/z*) = Puu (z) [B(z)B*(1/z*)] / [A(z)A*(1/z*)]. (6.7)
Входной возбуждающий процесс u[n] обычно не доступен для наблюдения и поэтому не может быть использован для целей спектрального анализа. Относительно него можно принять много различных допущений, скажем положить, что это единичный u[n] импульс, импульсная последовательность или белый шум. Если, например, использовано допущение о том, что это - импульс, то мы приходим к методам, которые описаны в гл.11. В данной главе мы будем полагать, что возбуждающая последовательность является белым шумом с нулевым средним значением и дисперсией pw, так что Puu(z)= pw. Тогда модель авторегрессии-скользящего среднего (АРСС) для временного ряда будет определяться выражением, где u[n] - последовательность, соответствующая белому шуму. Функциональная схема АРСС-модели показана на рис.6.1,а; здесь параметры a[k] характеризуют авторегрессионную часть этой модели, а параметры b[k] - ее часть, соответствующую скользящему среднему. Спектральную плотность мощности для АРСС-модели получаем, подставляя в (6.7) z=exp(j2pfT) и масштабируя интервалом отсчетов T, что дает
РАРСС(f)
= Trw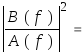 Trw
Trw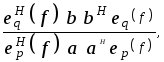 (6.8)
(6.8)
где полиномы A(f) и B(f) определяются выражениями
A(f)
= 1 + ![]() (6.9)
(6.9)
B(f)
= 1 + 
а векторы комплексных синусоид eq(f) и ep(f) и векторы параметров a и b имеют следующий вид:
ep(f)
=
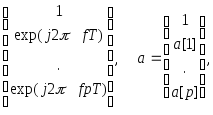 (6.10)
(6.10)
eq(f)
=
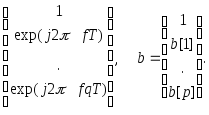
Спектральная плотность мощности АРСС-процесса вычисляется в диапазоне частот -1/2T£ f £1/2T.
В литературе часто используется обозначение АРСС(p,q), что удобно для краткого обозначения АРСС-модели с параметрами авторегрессии порядка p и параметрами скользящего среднего порядка q. Заметим, что задание АР-параметров, СС-параметров и дисперсии белого шума pw полностью характеризуют спектральную плотность мощности АРСС-процесса x[n] . Любой аддитивный шум наблюдения, присутствующий в последовательности измеряемых данных, должен моделироваться как шум источника возбуждающего шума, являющегося составной частью АРСС-модели. Эффекты, обусловленные шумом наблюдения, обсуждаются в гл.8.
рисунки 6.2
Если все АР-параметры положить, за исключением a[0]=1, равными нулю, то тогда
x[n]
=![]() (6.11)
(6.11)
будет строго СС-процессом порядка q, или просто СС(q)-процессом. Полагая в уравнении (6.8) p=0, получаем спектральную плотность мощности СС-процесса
Pcc
(f) =Trw![]() Trw
Trw![]() (6.12)
(6.12)
Функциональная схема СС-модели показана на рис.6.1,в.
Если все СС-параметры положить, за исключением b[0]=1, равными нулю, то
x[n]
= - ![]() (6.13)
(6.13)
будет строго АР-процессом порядка р, или просто АР(р) - процессом. Полагая в уравнении (6.8) q=0, получаем спектральную плотность мощности АР-процесса:
PАР
(f) = 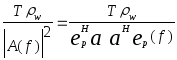 (6.14)
(6.14)
Функциональная схема АР-модели показана на рис.6.1,г. При заданных значениях параметров и дисперсии белого шума rw спектральные плотности мощности АРСС-, СС-, АР-процессов можно вычислить с помощью подпрограммы ARMAPSD, приведенной в приложении 6.А.
На рис. 6.2 показаны спектры типичных АРСС-, СС-, АР-процессов. Отметим острые пики, характерные для АР-спектров, и глубокие провалы, характерные для СС-спектров. АРСС-спектр, показанный на рис.6.2,в представляет собой результат объединения АР- и СС-спектров, показанных на на рис.6.2,а и 6.2,б. АРСС-спектр пригоден для моделирования как острых пиков, так и глубоких провалов. С несколько иной трактовкой спектральных характеристик этих параметрических моделей можно познакомиться в статье Гутовски и др. [2] и книге Кея [3].
