Лабораторная работа №8(1) / Lab1

Лабораторная работа №1.

Задание:

N=6

Описание сигнала
Гармонический сигнал с частотой A с нормально распределенным шумом (randn)	Для четных и нечетных вариантов
Гармонический сигнал, частота которого меняется по закону At^3+Bt^2+Ct+D	Для четных вариантов
	Для нечетных вариантов
Синусоида с меняющейся частотой от A до B по законам С и D	Для четных вариантов
	Для нечетных вариантов
Синусоида с частотой меняющейся скачкообразно: первая частота А, далее B, C и D	Для четных вариантов
	Для нечетных вариантов

Параметры
A	B	C	D	ШАГ
N*10 Гц				1/(5*N)
2*N	5	3*N	1	1/1024
1	3*N	5	10*N	1/1024
5*(N+5)	100*N	линейный	квадр.	1/1024
2*N	120-N	линейный	Exp	1/1024
10*N	20-N	30+2*N	70-3*N	1/1024
100	20*N	10*N	20+N^2	1/1024

2. Написать программу, вычисляющую свертку двух сигналов, оформить ее в виде функции Z=myCONV(A,B). Сравнить результаты работы программы с функцией conv(A,B).

3. Для сигналов найти свертки (используя свою программу) в соответствии с заданием.

A={…0,1,1,1,1,1,0,…}

B={…,0,1,2,3,0,…}

C={…,0,2,1,0.5,0,…}

D={…,0,1,2,3,4,5,0,…}

E={…,0,5,4,5,3,1,0,…}

F=sin(2*pi*t)+0.1*randn(1,length(t)); t=0:1/125:10;

G={…,0,2,1,2,0,…}

1. A*A

2. B*C; C*B

3. (D*E)*B; D*(E*B)

4. D*(E+B); D*E+D*B

5. F*A

6. F*G

Рассмотренные сигналы:

1. Для первой части работы были рассмотрены следующие сигналы: гармонический сигнал с частотой A (где A=6*10 Гц, шаг 1/(5*6)) с нормально распределенным шумом (randn) и гармонический сигнал, частота которого меняется по закону At^3+Bt^2+Ct+D, где A=2*N=12, B=5, C=3*N=18, D=1, шаг 1/1024.

2. Для второй части работы были рассмотрены сигналы B={…,0,1,2,3,0,…} и C={…,0,2,1,0.5,0,…}, B*C.

Генерация сигналов

1. Гармонический сигнал с частотой 60 Гц, шагом 1/30 с нормально распределенным шумом и гармонический сигнал, частота которого меняется по закону 12t^3+5t^2+18t+1, шаг 1/1024.

Реализуем генерацию сигналов средствами программы MATLAB и построим графики полученных сигналов:

n = 102; % длина реализации первого сигнала

n1=1024; % длина реализации второго сигнала

f1=60; % частота первого сигнала

t1 = (0:n-1)/30; % шаг дискретизации первого сигнала

t2 = (0:n1-1)/1024; % шаг дискретизации второго сигнала

f2 = linspace(55,600,1024);

t3=0;

% входная последовательность - полигармонический сигнал и случайный шум

ya=cos(f1*t1);

y1 = ya + randn(1,n);

% входная последовательность - гармонический сигнал,частота которого меняется по

% закону At^3+Bt^2+Ct+D, где A=2*N=12, B=5, C=3*N=18, D=1

while t3<n1

yb(1,t3+1)=cos(12*t2(1,t3+1)*t2(1,t3+1)*t2(1,t3+1)+5*t2(1,t3+1)*t2(1,t3+1)+18*t2(1,t3+1)+1);

t3 = t3+1;

end;

y1 = y1' ; % транспонируем вектор первой последовательности

y2 = yb'; % транспонируем вектор второй последовательности

% построение графиков полученных сигналов

figure(1);

clf, plot(t1,y1);

grid on;

xlabel('Time');

ylabel('Amplitude');

title('Harmonic signal');

figure(2);

clf,plot(t2,y2);

grid on;

xlabel('Time');

ylabel('Amplitude');

title('Harmonic signal (frequence law 12*t*t*t+5*t*t+18*t+1)');

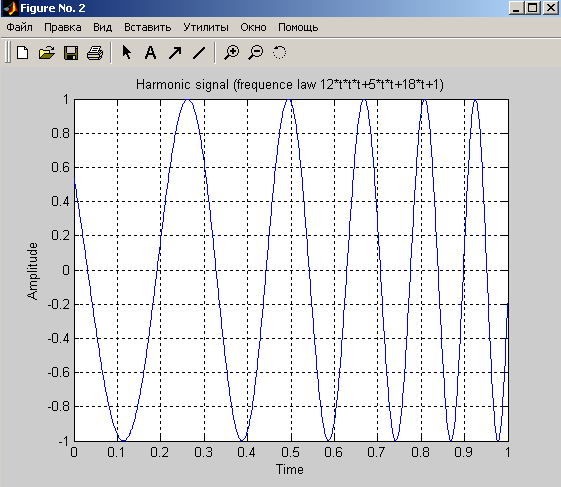
2. Сигналы B={…,0,1,2,3,0,…} и C={…,0,2,1,0.5,0,…}

Реализуем генерацию сигналов средствами программы MATLAB и построим графики полученных сигналов:

% входная последовательность y4 - сигнал вида B={...,0,1,2,3,0,...}

% входная последовательность y5 - сигнал вида C={...,0,2,1,0.5,0,...}

n3=512;

y4 = (0:n3-1);

y5 = (0:n3-1);

i=1;

while i<=n3

y4(1,i)=0; y5(1,i)=0;

y4(1,i+1)=1; y5(1,i+1)=2;

y4(1,i+2)=2; y5(1,i+2)=1;

y4(1,i+3)=3; y5(1,i+3)=0.5;

i=i+4;

end;

% построение графиков полученных сигналов

figure(5);

t5 = (0:n3-1)/512;

clf, plot(t5,y4);

grid on;

xlabel('Time');

ylabel('Amplitude');

title('Signal 1');

figure(6);

clf,plot(t5,y5);

grid on;

xlabel('Time');

ylabel('Amplitude');

title('Signal 2');

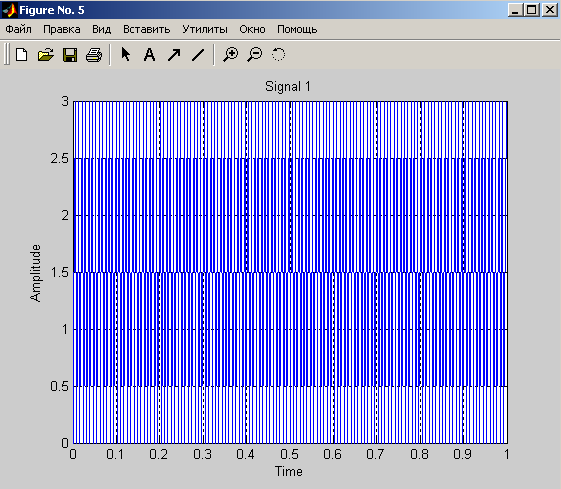
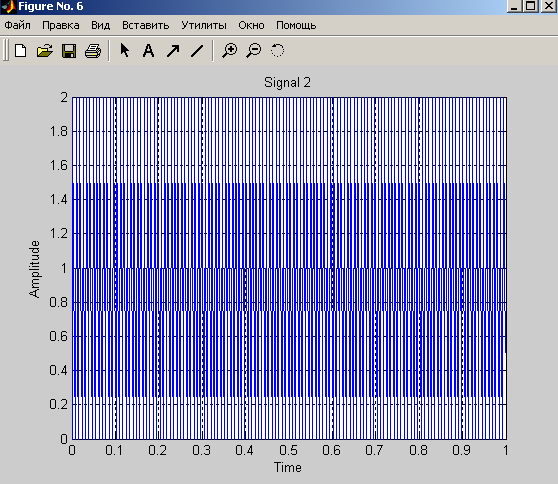
Нахождение свёртки с помощью стандартной функции conv(A,B)

1. Для гармонического сигнала с частотой 60 Гц, шагом 1/30 с нормально распределенным шумом и гармонического сигнала, частота которого меняется по закону 12t^3+5t^2+18t+1, шаг 1/1024

% нахождение свёртки рассматриваемых сигналов с помощью стандартной

% функции

d=conv(y1',y2');

figure(3);

t3 = (0:n+n1-2)/1024;

clf, plot(t3,d);

grid on;

xlabel('Time');

ylabel('Amplitude');

title('Convolution');

2. Для сигналов B={…,0,1,2,3,0,…} и C={…,0,2,1,0.5,0,…}

% нахождение свёртки рассматриваемых сигналов с помощью стандартной

% функции

s=conv(y4,y5);

t4 = (0:n3+n3-2)/1024;

figure(7);

clf, plot(t4,s);

grid on;

xlabel('Time');

ylabel('Amplitude');

title('Convolution');

Нахождение свёртки с помощью реализованной функции myConv(y1,y2)

Функция, которая реализует свертку, имеет вид:

function [myconv] = myConv(y1,y2)

k=0;m=0;

n = length(y1);

n1 = length(y2);

myconv =(0:n+n1-2);

while k<=n+n1-2

myconv(1,k+1)=0;

m=-n-n1+2;

while m<=k

if (m>=0 & m<=n-1 & k-m>=0 & k-m<=n1-1)

myconv(1,k+1)=myconv(1,k+1)+y1(1,m+1)*y2(1,k-m+1);

end;

m=m+1;

end;

k=k+1;

end;

1. Для гармонического сигнала с частотой 60 Гц, шагом 1/30 с нормально распределенным шумом и гармонического сигнала, частота которого меняется по закону 12t^3+5t^2+18t+1, шаг 1/1024

% нахождение свёртки рассматриваемых сигналов с помощью реализованой

% функции myConv(y1,y2)

y1=y1';y2=y2';

myconv =myConv(y1,y2);

figure(4);

t4 = (0:n+n1-2)/1024;

clf, plot(t4,myconv);

grid on;

xlabel('Time');

ylabel('Amplitude');

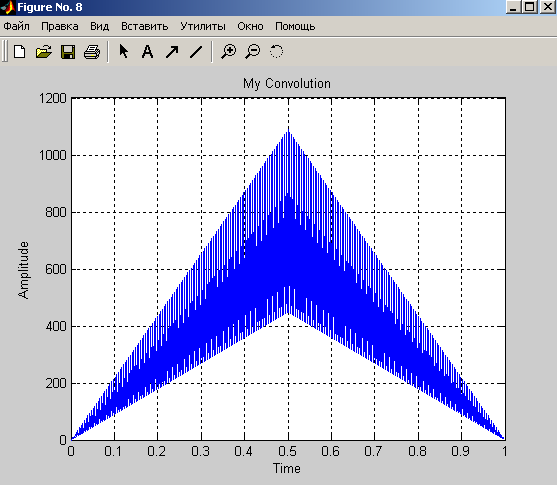
title('My Convolution');

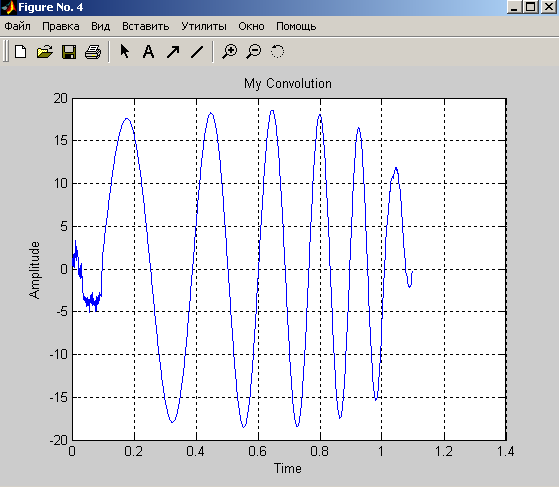
2. Для сигналов B={…,0,1,2,3,0,…} и C={…,0,2,1,0.5,0,…}

% нахождение свёртки рассматриваемых сигналов с помощью реализованой

% функции myConv(y1,y2)

k=0;m=0;

myconv1 =myConv(y4,y5);

figure(8);

t5 = (0:n3+n3-2)/1024;

clf, plot(t5,myconv1);

grid on;

xlabel('Time');

ylabel('Amplitude');

title('My Convolution');