ГрафиКон’99 Москва, 26 августа – 1 сентября 1999

9-я Международная Конференция по Компьютерной Графике и Машинному Зрению ГрафиКон’99 Москва, 26 августа - 1 сентября 1999 г.

Учебный курс

Вейвлет-анализ и его приложения

Леонид Левкович-Маслюк,

ИПМ РАН, Москва,

[e-mail]

Антон Переберин,

ИПМ РАН, Москва,

[e-mail]

Лекция 4

Биортогональные вейвлеты, лифтинг, мультивейвлеты

• Биортогональный кратномасштабный анализ

• Лифтинг

• Мультивейвлеты

Биортогональный кратномасштабный анализ

Существует более гибкая конструкция КМА, где класс допустимых фильтров шире, их коэффициенты проще вычислить, они могут быть симметричными и обладать другими полезными свойствами. Это – биортогональный кратномасштабный анализ, БКА.Быстрый алгоритм Малла сохраняется, но при разложении и восстановлении используются разные пары фильтров. Каждой паре соответствует КМА со своими скейлинг-функцией и вейвлетом. Но эти КМА не ортогональны – сдвиги скейлинг-функций и вейвлетов не ортогональны друг другу. Это означает, между прочим, что погрешность, внесенная при сжатии, может увеличиваться при восстановлении.

Рассмотрим две пары фильтров: и . Мы хотим проводить разложение при помощи свертки с , а восстановление – при помощи (в ортогональном случае ). Запишем условия точного восстановления (см. начало лекции 1). В терминах -преобразования разложение на высокие и низкие частоты с прореживанием вдвое имеет вид:

Записав в аналогичном виде процесс восстановления с помощью пары , приравняв результат к , и подставив , получим условия на ДПФ искомых фильтров:

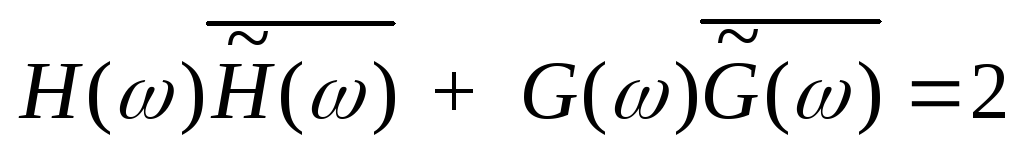• (1)

• 

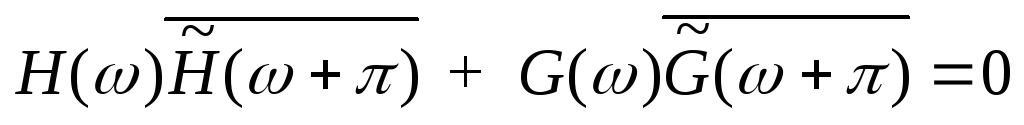
Вводя матрицы

, ,

запишем эти условия в виде:

(1’)

Посмотрим на скейлинг-функции, получаемые из этих фильтров. Напишем уравнения рескейлинга:

(2)

Их решения ищутся при помощи такого итерационного процесса: сначала в правую часть подставляется единичная ступенька (скейлинг-функция Хаара), затем – результат этой подстановки, сжатый вдвое по , и т.д. Мы видели, что предельная функция определяет ОКА только если имеет очень специальный вид. Для БКА выбор возможных фильтров шире, но тоже требуются дополнительные условия, при которых имеет место сходимость итераций, а предельные функции образуют базис. Предположим, что все эти условия выполнены, и определим биортогональные вейвлеты формулами:

(3)

Функции , называютосновными (primary), функции , –дуальными (dual).Взаимосвязь основных и дуальных функций, вытекающая из (1), такова: при всех целых

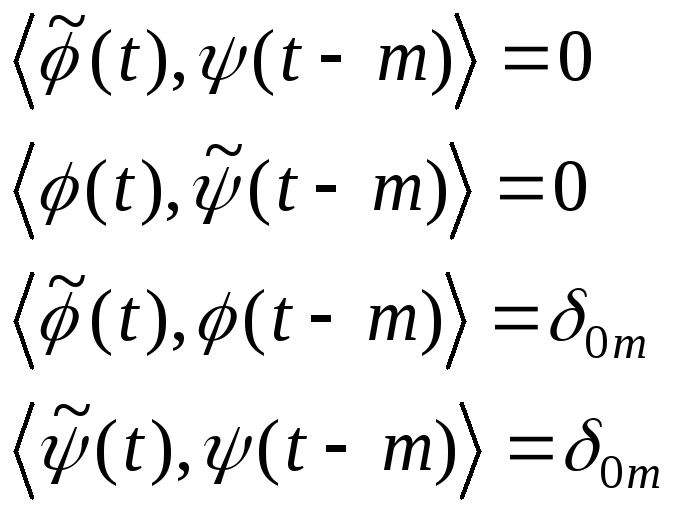(4)

Грубо говоря, сдвиги основных функций ортогональны сдвигам дуальных функций, но не ортогональны между собой. Пространства и , порожденные базисами и , удовлетворяют всем условиям ОКА, кроме последнего. Пространства и , порожденные и , дают разложения и сигналов в сумму сглаженных версий и деталей. Из (2) и (3) следует, что скейлинг-базисы и пространств и , а также вейвлет-базисы и всего пространства являютсядуальными друг к другу в смысле линейной алгебры (скейлинг-базисы – на одном и том же масштабе, вейвлет-базисы – на всех масштабах):

,

.

() не обязаны быть ортогональными к (). Однако возможен такой случай, когда базисы из сдвигов скейлинг-функций и вейвлетов в каждом из этих подпространств не ортогональны, а сами подпространства ортогональны; такой КМА называетсяполуортогональным (semiorthogonal).

В случае БКА коэффициенты разложения сигнала по основным функциям – это скалярные произведения сигнала с дуальными функциями:

.

Поэтому, чтобы спроектировать сигнал на , надо вычислить его скалярные произведения с базисными функциями , а на – с базисными функциями . Коэффициенты соответствующих разложений имеют вид:

, (5)

В лекции 1 были введены матрицы и ; определив аналогичным образом и , получим условие точного восстановления в виде:

(6)

Схемы разложения и восстановления получаются из схем для ОКА заменой операторов разложения на и .

В заключение этого раздела приведем популярный пример серии БКА, где и являются сплайнами. Достаточно построить и , удовлетворяющие условию

,

и положить

, .

Как и в ортогональном случае, должны выполняться некоторые дополнительные условия (которые мы здесь не уточняем), гарантирующие сходимость, регулярность и базисность решений уравнений рескейлинга (2) – (3). Кроме того, желательно, чтобы вейвлет, используемый для разложения (т.е. ), имел хоть несколько нулевых моментов, а вейвлет и скейлинг-функция, используемые длявосстановления(и были как можно более гладкими. Имеется решение, удовлетворяющее всем этим требованиям. Это решение использует сомножители того тригонометрического многочлена, который был использован для построения вейвлетов Добеши.

Семейство фильтров имеет вид:

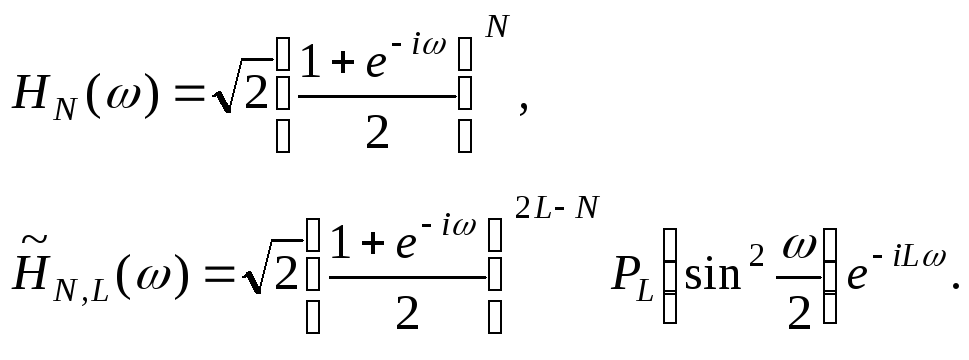
Скейлинг-функция является B-сплайном. На рис. 1 показаны скейлинг-функции и вейвлеты БКА, полученного при .

Р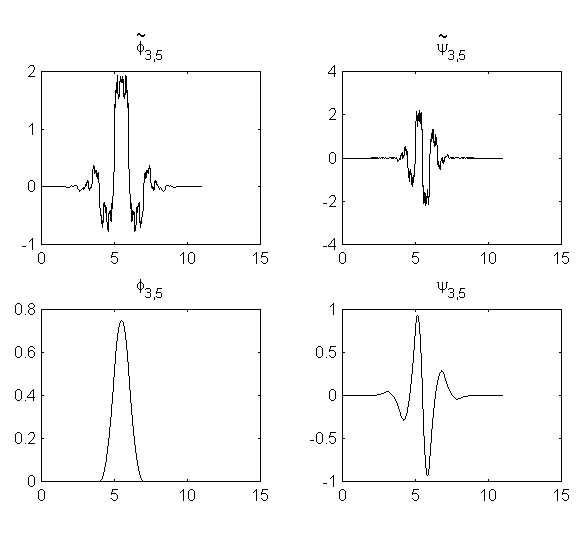исунок 1.

Биортогональные вейвлеты и скейлинг-функции.

Ясно, что гладкость функций, порождающих дуальный МА, очень низка. При увеличении Lполучаются более гладкие функции, однако и длина фильтров соответственно увеличивается.